基于等距面模型的叶片精密测量方法研究

北京航空航天大学机械工程及自动化学院 王军伟 宁 涛 陈志同

随着叶片加工精度与自动化程度的不断提升，应用三坐标测量机实现叶片几何精度的测量已成为一种常用工艺。但是测量机在测量过程中只能得到测头球心的坐标，而测头与叶片的实际接触点及其法矢是未知的。针对此情况，传统测量方法是按照理论测量点所在曲面的法矢对测头球心点进行半径补偿，该补偿方法只有在理论模型与实际叶片模型完全重合时才不会导致补偿误差。但是考虑到叶片检测中的定位误差以及叶片加工变形的存在，如图1所示，理论模型St与实际模型Sr并不重合，测头与被测叶片实际接触点pr的法矢nr与理论测点pt的法矢nt方向也不同，因此按理论法矢nt对测头球心点ps进行测头半径补偿得到的补偿点pc并非被测叶片上的点，这样就导致了补偿误差。

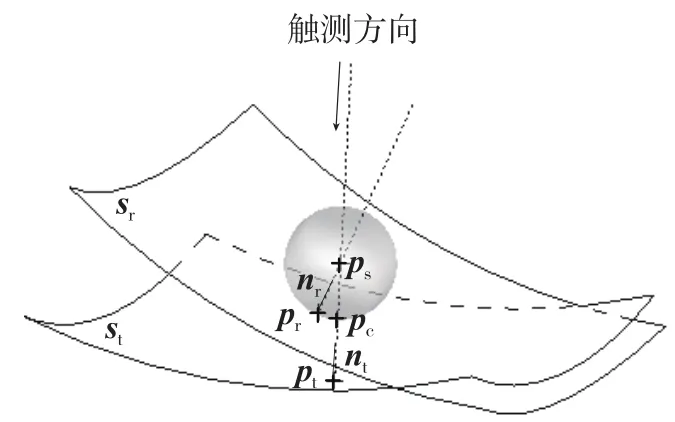
图1 测量误差

提高测头与叶片实际接触点法矢方向的估计精度是提高叶片测量精度的一个求解方向。微平面法[1]与微球面法[2]均是通过测量被测点周围的若干点来估计被测点处法线方向的。这两种方法原理类似，可一定程度上减小补偿误差，但是都存在测量不确定度影响求法线方向的问题[3]，且两种方法测量过程繁琐，测量数据处理复杂。Menq等[4]提出了一种迭代测量的方法，通过反复测量来不断修正测量方向，该方法虽然提高了测量精度，但测量时间也相应增加，测量效率大大降低。曲面拟合法[5]是通过拟合测头球心曲面Ss，然后在测头球心曲面上得到相应点的法线方向。该方法避免了其他方法的不足，并不针对单个的测量点进行补偿，而是通过拟合测头球心曲面进而求得被测曲面的。基于该方法的思想，本文提出了一种基于等距面几何模型的叶片测量方法。

基于等距面模型的叶片测量方法原理

设叶片理论模型为St（u，v），其等距面模型为St'（u，v）；叶片实际模型为Sr（u，v），其等距面模型为Sr'（u，v）。则可以得到：

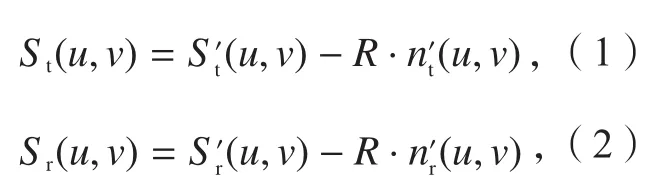
其中：R为测头半径，nt'（u，v）为St'（u，v）的单位法矢，nr'（u，v）为Sr'（u，v）的单位法矢。

基于等距面几何模型叶片测量方法的原理如下：

（1） 根据式（1）求出St'（u，v），并以St'（u，v）为指导模型，进行测量路径规划，得到理论测量点集p'ti（i=1，2，3，…）及其触测方向，如图2（a）所示；

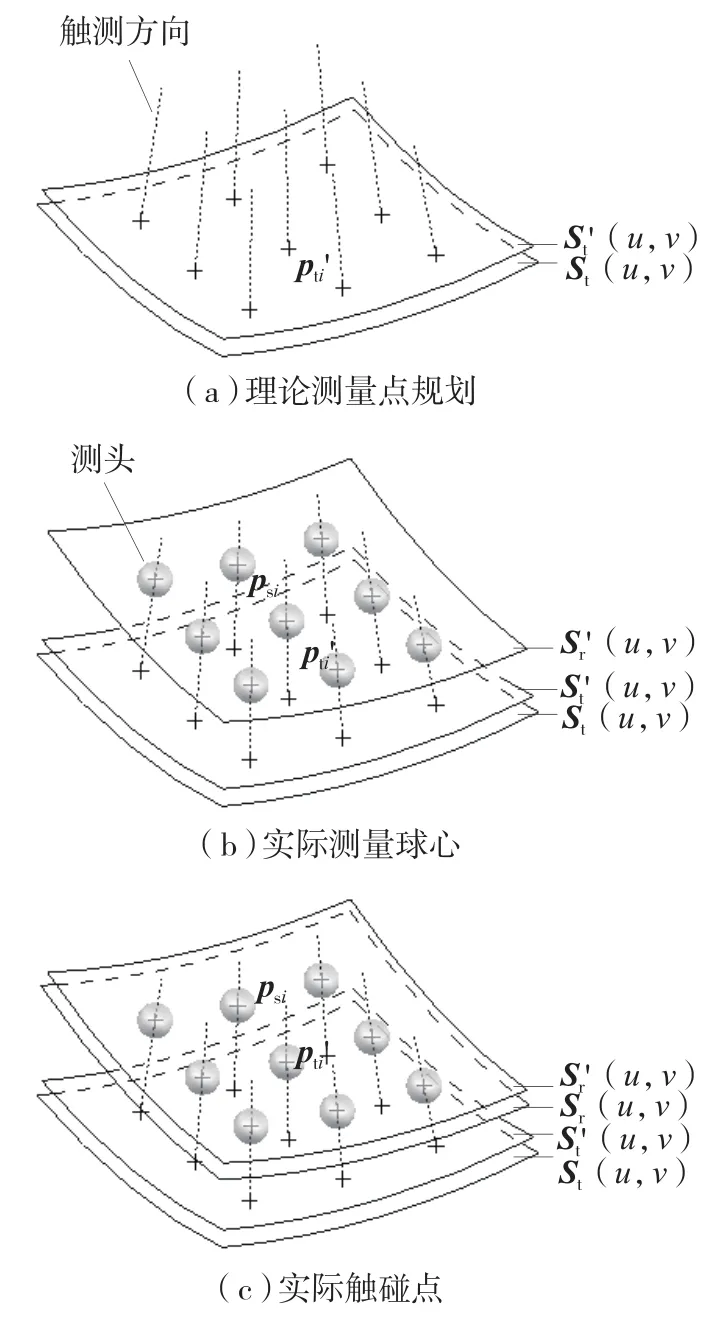
图2 测量方法原理

（2）用半径为R的测头进行测量，将得到的测头球心点集psi（i=1，2，3，…）进行插值构造曲面Sr'（u，v），如图 2（b）所示；

（3） 根据式（2）求出Sr（u，v），如图2（c）所示。

（4）比较Sr（u，v）与St（u，v）得到被测叶片的加工误差分布。

与传统的叶片测量方法相比较，该方法不会因为实际叶片与理论模型的差异而导致测量误差，更加适用于叶片的测量，且叶片定位误差以及叶片加工变形等问题对该方法影响较小。另外，应用该方法进行测量，以可行的不同触测方向ni·k，逼近理论测量点p'ti，根据式（2）可知，测头球心点psi·k均位于Sr'（u，v）上，如图3所示，增加了测量路径规划的灵活性，减少了实际测量中测头逼近方向的限制。

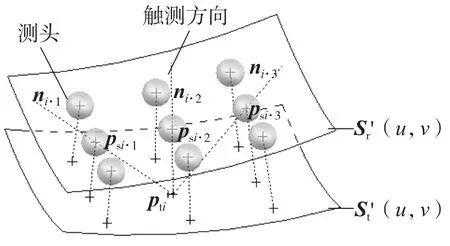
图3 以不同触测方向测量

基于等距面模型的叶片型面CMM测量

叶片型面CMM测量主要分为测量路径规划、测量和数据处理3个阶段。

1 测量路径规划

为了降低数据处理的复杂度，提高曲面拟合的精度，基于二维约束，按照“曲面—曲线—点集—测点集”的分解次序，实现从曲面到测点集的分解。具体的测量路径规划方法步骤如下：

（1） 求取理论叶片型面St的等距面St'，距离为测头半径R；

（2）用截平面法在St'上选取适当的测量线集L，测量线数为N，具体算法如图4所示；

（3）将各测量线li离散成测量点集Pi，其中i=1，2，…，N，具体算法如图5所示；

（4）求各测量点所在测量线处的二维法矢方向作为测头触测方向。

上述测量路径规划方法，以最优替代曲面原则进行测量点布局，更好地代表了曲面特征，且保证同一测量线对应的测头球心点均处于同一平面内。因此，曲面拟合的过程可以分解为二维平面中的测量点拟合成线以及三维空间中的线拟合成面两个步骤，避免了传统曲面拟合法点云直接拟合成面所需大量测量点，且测量点无规律的弊端，降低了数据处理的复杂度，提高了曲面拟合的精度。

2 叶片测量

测量坐标系建立的准确性是影响测量精度的一个重要因素。当叶片加工变形过大、基准过小就会导致叶片初始测量基准不准，实际测量中可能造成叶片前后缘采点失败，甚至中断测量。为了确保测量过程的连续性以及进一步的提升测量精度，在实际测量环节中增加了测量坐标系的配准定位，并提出了一种新的定位方法。该定位方法可精确地按误差最小原则配准叶片型面的测量坐标系。

由于对测量坐标系的配准定位并不需要大量的测量点，因此为提高测量效率，以及在叶片发生弯扭变形时，能够保证定位精度，故选择已规划测量点中上下两条边界测量线以及中间部位的一条测量线上的测量点进行测量即可。

（1）叶片定位。

设叶片型面模型为S（u，v），则其等距面S'（u，v）可表示为：

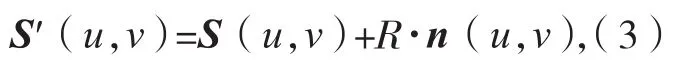
其中：R为距离，n（u，v）为曲面单位法矢。

图4 选取测量线算法

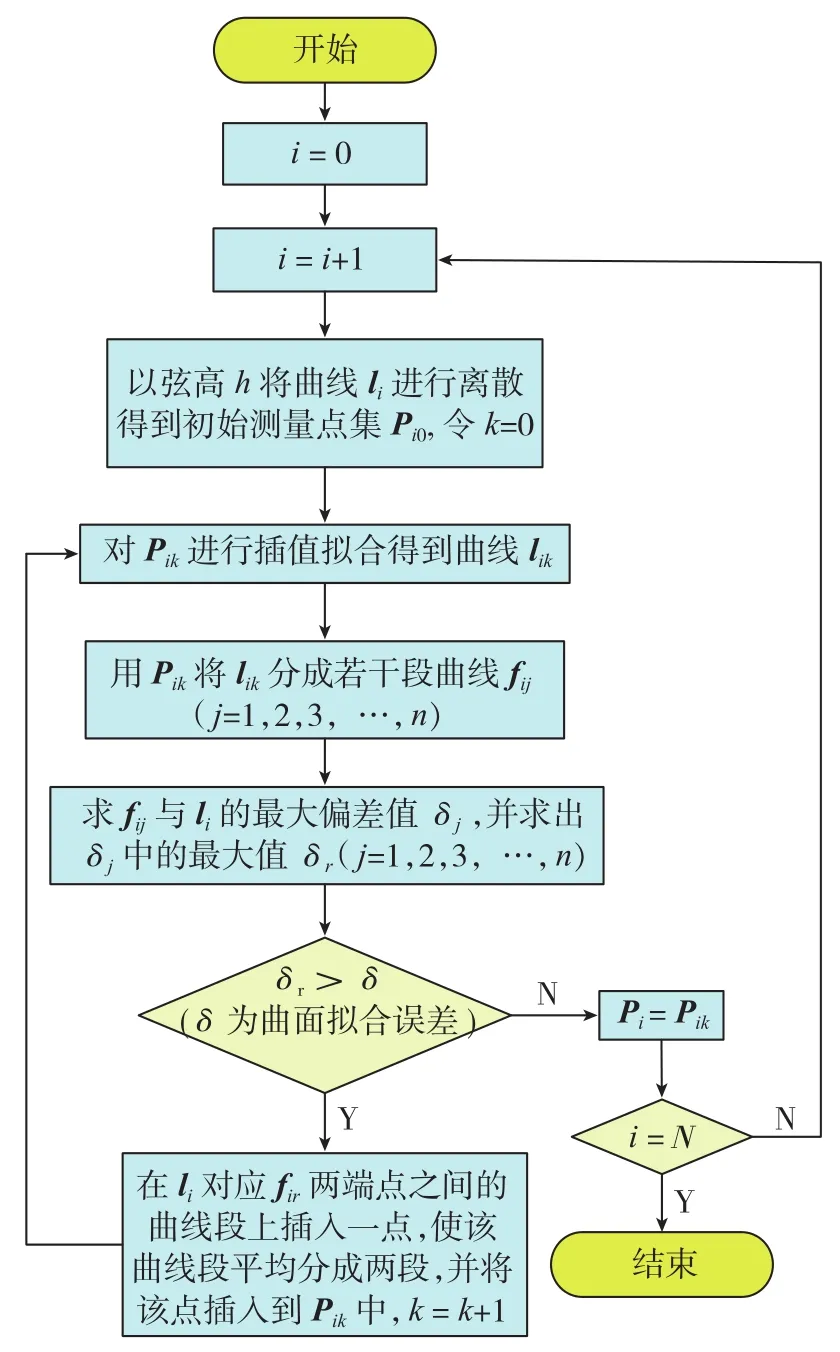
图5 选取测量点算法

假设叶片理论模型曲面为S1（u，v），其等距面为S1'（u，v）；叶片实际型面为S2（u，v），其对应的等距面为S2'（u，v）。如果曲面S2（u，v）经变换矩阵T刚性变换后为S1（u，v），则可得到：

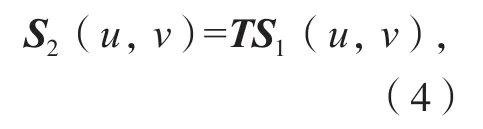
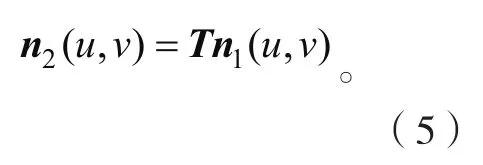
根 据 式（3）、（4）、（5），可得到：

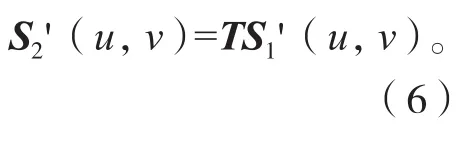
因此，可得出两曲面之间的变换关系与其对应的两等距面之间的变换关系对等。

传统的定位方法采用补偿后的测点与理论模型进行最佳拟合定位，但是补偿后的数据存在误差，必然会降低定位的准确性。本文提出的定位方法采用无补偿的测头球心点作为测量点数据，与叶片理论模型等距面（距离为测头半径）进行最佳拟合定位，以得到坐标变换矩阵T。根据上述的推导，可知将初始坐标系按变换矩阵T进行变换，即可使理论模型与实际叶片达到最佳匹配，提高了叶片定位的准确性。

（2）最佳拟合定位。

最佳拟合定位就是通过测量数据与CAD理论模型进行精确匹配，即通过精确匹配使叶片实测点相对于理论模型的误差达到最小，从而减小系统误差的影响。

测量数据点集P与理论模型间的变换映射关系，可以转换为点集P与理论模型上的对应的最近点集Q间的旋转平移变换，故测量数据点与叶片CAD理论模型匹配采用最近点的欧式距离平方和作为目标函数，定义为：

其中：qi为测量点pi对应CAD理论模型上的点坐标，为pi距模型上最近的点；R为旋转矩阵；T为平移矢量。

具体的匹配过程描述如下：

·初始迭代时，令点集初始位置P0=P，k=0，d0=0 。

·迭代执行以下步骤，直到符合条件。

① 计算最近点集Qk=C（Pk，S）；

② 求解点集P到点集Qk的旋转矩阵Rk和平移向量Tk；

③ 将点集P按Rk和Tk进行旋转平移变换得到新的位置Pk+1=Rk P+Tk；

④ 求点集Pk+1到理论模型S的欧式距离平方和dk+1=F（Pk+1，S）；

⑤ 如果满足给定的阈值，｜dkdk+1｜≤ε，终止迭代。Rk和Tk就是所求旋转矩阵和平移矢量。否则k=k+1，转①。

上述解法的关键就是步骤①的求解最近点集和步骤②的求解旋转平移矩阵。为了实现程序的人机交互，可依托于UG的二次开发平台，用标准的ICP算法作为基本算法来实现测量数据点与理论CAD模型的匹配。

（3）测量。

具体测量步骤如下：

·将叶片测量件以适当的方式固定在三坐标测量机平台上，在测量软件Metrology XG7下，手动测量得到叶片的加工基准特征，以此建立初始测量坐标系。

·开启自动测量模式，对已规划好的测量点中上下两条边界测量线以及中间部位一条测量线上的测量点进行采样，按上文所述的定位方法进行定位，即可得到变换矩阵T，修改初始坐标系，建立精确坐标系。

·在精确坐标系下，对已规划的所有测量点进行测量，测量完毕之后，将测量数据导出，用于后续数据处理。

3 测量数据处理

由于对测头触测方向进行了约束，得到同一测量线的测量球心点均位于同一平面，对后续的实际叶片造型提供了方便。基于NURBS造型理论，借助于UG自由曲面造型平台，具体处理步骤如下：

（1） 基于UG平台，针对每条测量线得到的测量点进行样条插值拟合；

（2） 将第一步得到的拟合曲线通过曲线组命令拟合成面；

（3） 将拟合得到的曲面向内偏置一个测头半径的值得到该曲面的等距面。

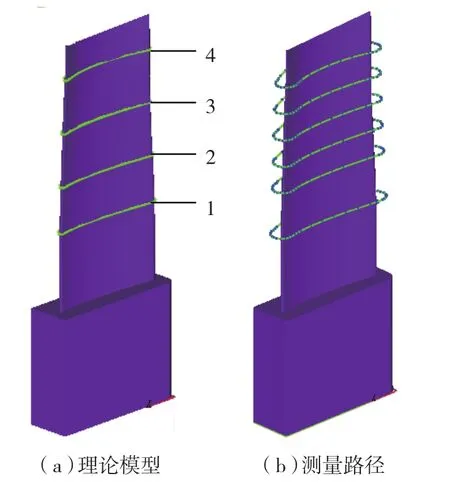
图6 测量点规划

按以上步骤得到的等距面即为实际叶片的拟合模型，可直接对该模型与理论叶片模型进行面分析，即可得到实际叶片加工质量的有关信息。如将实际叶片拟合模型与理论截面线所在平面相交，可得到相应的实际叶片拟合截面线，与理论截面线进行分析比较，也可得到线轮廓度、叶型扭转误差以及位置度误差等信息。

实例

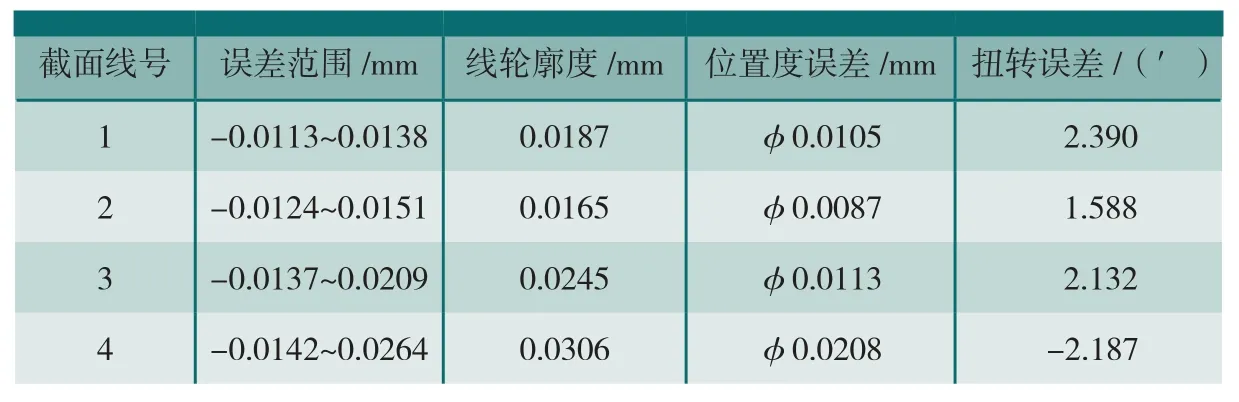
表1 传统方法分析结果

表2 本文方法分析结果

以某型发动机叶片为例，采用传统测量方法以及本文方法对同一叶片进行了测量。本文测量方法测量点规划如图 6所示，图中1、2、3、4为理论截面线。

当理论指导模型与被测件完全重合时，传统测量方法的测量误差为0。比较两种测量方法的测量精度，分别以两种测量方法的测量结果拟合实际叶片曲面，并以拟合曲面作为指导模型，采用传统测量方法再次进行测量。表1为传统测量方法拟合曲面作为指导模型的测量分析结果，表2为本文方法。从表中数据可以得出：本文方法拟合曲面较传统方法拟合曲面更接近实际被测叶片，证明了本文方法较传统方法有效的提高了测量精度。

结论

针对传统叶片测量方法中存在的测头半径补偿误差问题，本文提出了一种基于等距面模型的叶片测量方法，并给出了具体的测量工艺方案。提出的二维约束测量路径规划方法，避免了传统曲面拟合法点云直接拟合成面所需大量测量点，且测量点无规律的弊端，降低了数据处理的复杂度，提高了曲面拟合的精度；提出的精确定位方法较传统定位方法有效地提高了定位精度；最后通过实际测量试验验证了上述方法的有效性和实用性。试验结果表明本文测量方法较传统测量方法有效地提高了叶片测量的精度。

[1] SUH S H，LEE S K，LEE J J.Compensating probe radius in free surface modeling with CMM： Simulation and experiment.Int. J. Prod. Res.，1996，34(2)： 507-523.

[2] 颉赤鹰，陈少克. 三坐标测量机测头半径补偿的新方法. 组合机床与自动化加工技术，2006(1)： 50-52.

[3] 蔺小军，王增强，单晨伟. 自由曲面CMM测量测头半径补偿方法. 航空制造技术，2011(10)： 75-77，85.

[4] MENQ C，CHEN F L. Curve and surface approximation from CMM measurement data. Computers ind. Engng.，1996,30(2)： 211-225.

[5] MAYER J R，MIR Y A，VAFAEESEFAT A，et al. Touch probe radius compensation for coordinate measurement using kriging interpolation. Proc. Instn. Mech. Engrs.，1997，211(1)： 11-18.