基因遗传算法的多目标优化问题的研究与应用

高林娥

(运城师范高等专科学校，山西 运城 044000)

就现实而言，我们生存的世界存在许多问题，而在解决这些问题时，会遇到两种类型的困难，一是多个相互冲突的目标。二是高维复杂的搜索空间。就第一点而言，单目标优化不能解决的问题，多个相互竞争目标的优化结果是可以得到一组可行解，一般被称作Pareto最优解集［1］。经济的发展是迅速的，而人的潜能是巨大的。人类为了更好的生活，在改造自然的方案规划和设计的过程都体现了效益最大化和成本最小化的这一基本优化原则。在现实生活中几乎每个重要的决策问题都要在考虑约束条件的同时对若干个相互冲突的目标进行有效的处理，但是这又往往涉及到多个目标的优化问题，这些目标不是单独存在的，而是联合在一起的相互竞争的目标［2］。所以，效益最大化和成本最小化在本质上是一个多目标优化问题。将遗传算法合理地应用到多目标优化的问题上，可以有效地解决问题。而这种将遗传算法应用到多目标优化问题上的算法通常称为多目标优化进化算法或者多目标优化遗传算法。由于多目标问题的广泛存在性和求解的困难性，所以研究者们一直对其有很大的兴趣和挑战性。它最早是由Franklin在1772年提出了如何有效协调多个目标矛盾的问题，但是目前国际上绝对多数的专家学者都普遍认为多目标优化的问题是由法国的经济学家V.Pareto在1896年最早提出来的，V.Pareto从政治经济学的角度出发，将许多难以进行比较的问题统一归纳为多目标的最优化问题。

1 多目标优化的综述

1.1 多目标优化的基本概念

在大多数情况下，单目标优化存在多个最优解，这种情况在多目标优化问题中是不存在的，多目标优化问题的最优解只存在Pareto最优解。若一个多项目优化问题存在所谓的最优解，则该最优解一定是Pareto最优解，并且Pareto最优解也只有这些最优解组成，不再包含其它解。因此Pareto最优解是多目标优化问题的合理的解集合。而通常多目标优化问题的Pareto最优解是一个合集。所以，在求解多目标优化问题的首要步骤和关键是求出尽可能多的Pareto最优解［3］。

1.2 目前常用的多目标优化方法

约束法:在MOP问题中，从k个目标函数f1(x)，f2(x)，…，fk(x)中，若能够确定一个主要的目标，例如f1(x)，而对其它的目标函数只要满足一定的条件即可，这样我们就可以把其它目标当作约束来处理。此外，还有加权法、距离函数法、分层序列法等。

1.3 传统优化方法应用时的注意问题

传统的多目标优化方法在解决问题的过程中通常会存在着一定的局限性，其具体表现主要有以下几点:①在运用加权法等一系列古典方法进行多目标优化问题的求解时，对Pareto最优前端的形状很敏感，但是却无法有效地处理前端的凹部。②通常情况下只能得到一个解，但是在实际决策中的决策者往往需要多种行之有效的方案来进行选择。③传统方法在运用的过程中都会共同存在着一个目标，那就是如何获得Pareto的最优集。而在获得这个Pareto的过程中，最优集需要多次进行优化，但是由于每一次的优化过程都是相互独立的事件，得出的结果也很难得到统一，使得决策者很难进行有效的决策，而且这种方法费时又费力。④多个目标函数之间的量纲不同，难以统一。⑤由于目标函数的各个权值是由人为规定的，因此加权值的分配有着很强的主观性。

2 遗传算法的基本原理和方法

2.1 遗传算法的概述

遗传算法是模拟生物界中自然选择和群体遗传机制，采用简单的编码技术来表示各种复杂的结构，并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。

2.2 遗传算法的运行流程

图1 遗传算法的运行流程

第一，编码。解空间的解数据x作为遗传算法中的一种表现形式，通常会将从表现型到基因型的映射称为编码［4］。遗传算法在搜索之前应当先将解空间的解数据表示成遗传空间的基因型串结构数据，这样一来。这些串结构中不同组合的数据就构成了各个不一样的点。第二，初始群体的生成。初始群体主要是由随机生成的N个串结构数据，这些串结构数据又会构成N个个体，N个个体再会构成一个群体。遗传算法在此时便会以这N个串结构作为迭代的初始点。第三，适应度值评价检测。适应度函数通常代表着个体或解的优越性。在处理不同的问题时，适应度函数定义的方法式也不尽。第四，选择合适的算子，并将此算子作用于群体，在确定个体时应当紧密依据适应度函数值的变化来进行确定，以便下一步操作的顺利进行。第五，交叉。把交叉算子运用到群体之中，并以交叉的概率P进行交叉操作，之后再随机对群体中的选取的个体在随机生成的位置进行交叉。第六，变异。通过将变异算子在群体中进行作用，在进行变异操作时，应当以变异的概率对个体进行变异，从而得到新个体。

3 多目标优化问题遗传算法应用示例

示例:

第一步:产生初始种群

s1=13(01101)

s2=24(11000)

s3=8(01000)

s4=19(10011)

第二步:计算适应度

假定适应度为f(s)=s2，则

f(s1)=f(13)=132=169

f(s2)=f(24)=242=576

f(s3)=f(8)=82=64

f(s4)=f(19)=192=361

第三步:选择

染色体的选择概率为:

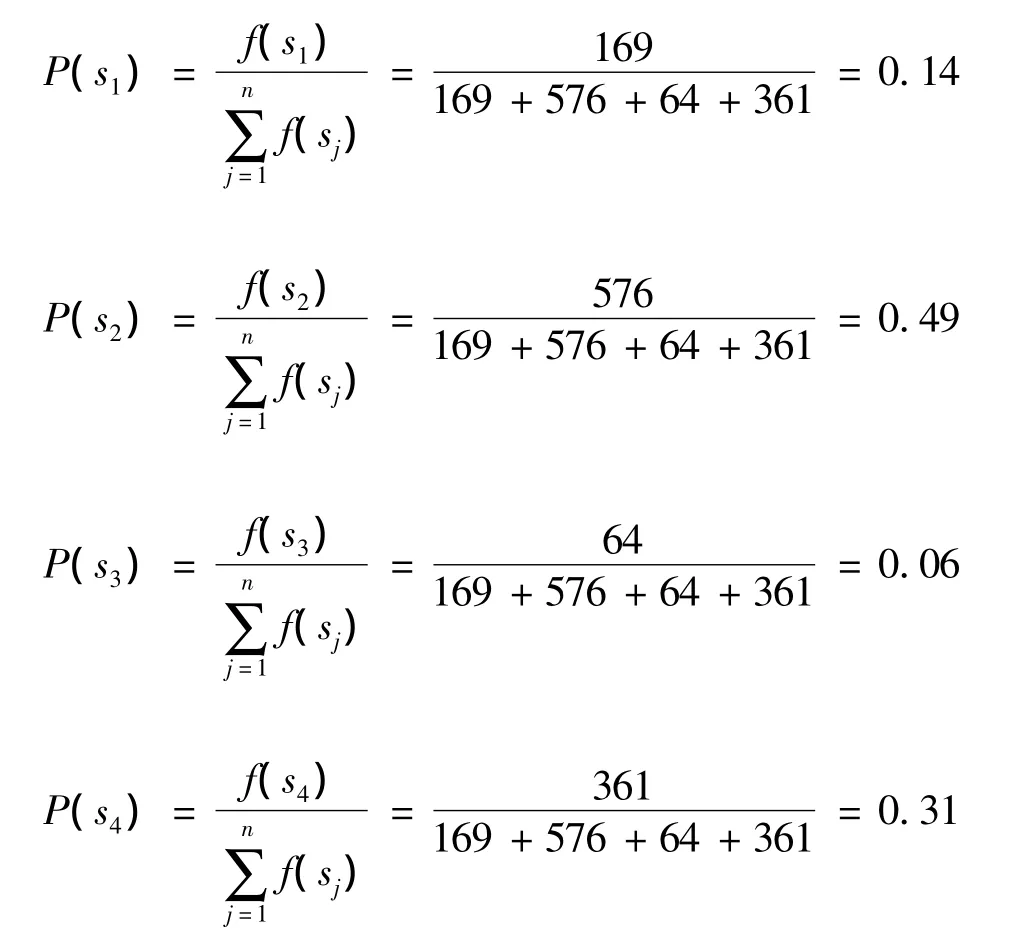
例如设从区间［0，1］中产生4个随机数:

r1=0.450126，r2=0.110347

r3=0.572496，r4=0.98503

染色体 适应度 选择概率 积累概率 选中次数S1=01101169 0.14 0.14 1 S2=11000 576 0.49 0.063 2 S3=01000 64 0.06 0.69 0 S4=10011361 0.31 1.00 1

第四步:交叉

基本遗传算法(SGA)中交叉算子采用单点交叉算子。

单点交叉运算

注:表中/为交叉点

第五步:变异

注:表中0、1为变异点。

第六步:至下一代，适应度计算——选择——变异，直至满足条件为止。

4 结论

基因遗传算法的多目标优化问题的关键在于群体适应度的分配和进化过程中群体多样性的保持。多目标优化问题的解不是唯一的，而是存在一个最有解集合，对于解决现实生活中的复杂问题是可行的。但是，目前求解的多目标优化问题的遗产算法缺乏收敛性理论，没有描述出多目标遗传算法代与代之间的动态［5］。多目标优化领域取得成果是瞩目的，但进一步的研究也将作为发展的趋势。

［1］黄孔亮.多目标遗传算法研究与应用［D］.深圳:深圳大学，2005.

［2］蓝盛芳.试论达尔文进化论与协同进化论［J］.生态科学，1995，(2).

［3］杨唐胜，陈文清，朱瑞赓.一种与遗传算法类似的人工免疫算法［J］.武汉理工大学学报，2005，(10).

［4］邓丽君.基于遗传算法的多目标优化与决策方法研究［D］.长沙:国防科学技术大学，2003.

［5］关志华.面向多目标优化问题的遗传算法的理论及应用研究［D］.天津:天津大学，2002.