导数与定积分命题规律与备考策略

高慧明 季飞

本专题全国高考客观题主要考查函数的基本性质、函数图像及变换、函数的零点、导数的几何意义、定积分（仅限理科）等为主，也有可能与不等式等知识综合考查;解答题主要是以导数为工具解决函数、方程、不等式等的应用问题.

理科在“函数导数与积分”的考查：2011年第9题利用定积分求面积，2012～2015年均没出现过定积分的试题，另外每年在第21题都是利用导数研究函数的性质，以求函数的单调性、极值、最值为主，考查不等式的相关问题.

函数、导数部分2011年有两个选择题，一个是判断函数单调性与奇偶性，另一个定积分求面积，2012年有两个选择题，一个是由解析式找图像，另一个是利用导数求切线、距离最值问题.2015年小题考了一个选择题和一个填空题，选择题考查利用导数研究函数的单调性，填空题考查基本的初等函数与函数的性质.

文科在“函数导数”的考查：函数的基本性质主要考查函数的单调性、奇偶性等，难度通常为中等，基本初等函数通常考查指数函数与对数函数，有时候会与函数的图像、函数与方程等相结合，考查数形结合思想的灵活应用，有时候也会融入导数的应用等，这类题目通常难度偏大，一般作为选择题或填空题的压轴题出现.

对导数的考查通常以函数的单调性、函数的极值或最值、不等式的证明或不等式恒成立问题为载体，考查导数的综合应用.在解决这类问题时，有时候需要对问题进行转化或构造相应的函数，因此对等价转化、数形结合的数学思想也有较高的要求，正确求出函数的导数，并灵活应用导致与单调性的关系是解题的关键.从这几年的命题规律来看，这一部分通常出现在第20题或21题的位置，题型比较稳定. 小题中主要考查基本初等函数、函数的性质等，而解答题中主要考查导数在解决函数问题中的综合应用，且或总会出现其一，小题中有时候也会对导数进行考查.

第一单元 变化率与导数、导数的计算

【考点聚焦】

本单元内容主要包括导数的概念、导数的几何意义、导数的计算.

【经典解析】

考点1：导数的计算

例1. 分别求下列函数的导数：

【收获与点评】 （1）本题在解答过程中常见的错误有：①商的求导中，符号判定错误;②不能正确运用求导公式和求导法则，在第（3）小题中，忘记对内层函数2x+1进行求导.

（2）求函数的导数应注意：

①求导之前利用代数或三角变换先进行化简，减少运算量;

②根式形式，先化为分数指数幂，再求导.

③复合函数求导先确定复合关系，由外向内逐层求导，必要时可换元处理.

考点2：导数的几何意义

例2. （1）若曲线y=kx+lnx在点（1，k）处的切线平行于x轴，则k=________.

（2）设f（x）=xlnx+1，若f ′（x0）=2，则f（x）在点（x0，y0）处的切线方程为____________________.

∴g′（x）<0，故g（x）在（0，1）上单调递减;

当x>1时，x2-1>0，lnx>0，g′（x）>0，g（x）单调递增.

所以，g（x）>g（1）=0（？坌x>0，x≠1）.

所以除切点之外，曲线C在直线l的下方.

【收获与点评】（1）准确求切线l的方程是本题求解的关键;第（2）题将曲线与切线l的位置关系转化为函数g（x）=x-1-f（x）在区间（0，+∞）上大于0恒成立的问题，进而运用导数研究，体现了函数思想与转化思想的应用.

（2）当曲线y=f（x）在点P（x0，f（x0））处的切线平行于y轴（此时导数不存在）时，切线方程为x=x0;当切点坐标不知道时，应首先设出切点坐标，再求解.  注意：

1. 理解导数的概念时，要注意f ′（x0），（f（x0））′与f ′（x）的区别： f ′（x）是函数y=f（x）的导函数， f ′（x0）是f（x）在x=x0处的导数值，是常量但不一定为0，（f（x0））′是常数而且一定为0，即（f（x0））′=0.

2. 对于函数求导，一般要遵循先化简再求导的基本原则.求导时，不但要重视求导法则的应用，而且要特别注意求导法则对求导的制约作用，在实施化简时，首先必须注意变换的等价性，避免不必要的运算失误.

3. 求曲线的切线时，要分清在点P处的切线与过点P的切线的区别.

第二单元 导数在研究函数中的应用

【考点聚焦】

本单元内容主要包括函数导数与单调性、导数与极值、导数与最值.

【经典解析】

考点1：利用导数研究函数的单调性

例1. 设函数f（x）=（x-1）ex-kx2.

（1）当k=1时，求函数f（x）的单调区间;

（2）若f（x）在x∈[0，+∞）上是增函数，求实数k的取值范围.

解析：（1）当k=1时，f（x）=（x-1）ex-x2，∴ f ′（x）=ex+（x-1）ex-2x=x（ex-2）.令f ′（x）>0，即x（ex-2）>0，∴ x>ln 2或x<0.令f ′（x）<0，即x（ex-2）<0，∴0

【收获与点评】 （1）可导函数y=f（x）在点x0处取得极值的充要条件是f ′（x0）=0，且在x0左侧与右侧f ′（x）的符号不同.（2）若f（x）在（a，b）内有极值，那么f（x）在（a，b）内绝不是单调函数，即在某区间上单调增或减的函数没有极值.

第三单元 导数的综合应用

【考点聚焦】

本单元内容主要包括利用导数解决生活中的优化问题、导数在研究方程和不等式中的应用.

【经典解析】

考点1：导数在方程（函数零点）中的应用

例1. 已知函数f（x）=x2+xsinx+cosx.

（1）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，求a与b的值;

（2）若曲线y=f（x）与直线y=b有两个不同交点，求b的取值范围.

【思维生长点】（1）由导数的几何意义，知f ′（a）=0且f（a）=b，解方程得a，b的值. （2）两曲线的交点问题，转化为方程x2+xsinx+cosx-b=0. 通过判定零点个数来求解.

解析：由f（x）=x2+xsinx+cosx，得f ′（x）=2x+sinx+x（sinx）′-sinx=x（2+cosx）.

（1）因为曲线y=f（x）在点（a，f（a））处与直线y=b相切，所以f ′（a）=a（2+cosa）=0，b=f（a）.

解得a=0，b=f（0）=1.

（2）设g（x）=f（x）-b=x2+xsinx+cosx-b.

令g′（x）=f ′（x）-0=x（2+cosx）=0，得x=0.

当x变化时，g′（x），g（x）的变化情况如下表：

所以函数g（x）在区间（-∞，0）上单调递减，在区间（0，+∞）上单调递增，且g（x）的最小值为g（0）=1-b.

①当1-b≥0时，即b≤1时，g（x）=0至多有一个实根，曲线y=f（x）与y=b最多有一个交点，不合题意.

②当1-b<0时，即b>1时，有g（0）=1-b<0，

g（2b）=4b2+2bsin2b+cos2b-b>4b-2b-1-b>0.

∴y=g（x）在（0，2b）内存在零点，

又y=g（x）在R上是偶函数，且g（x）在（0，+∞）上单调递增，

∴y=g（x）在（0，+∞）上有唯一零点，在（-∞，0）也有唯一零点.

故当b>1时，y=g（x）在R上有两个零点，

则曲线y=f（x）与直线y=b有两个不同交点.

综上可知，如果曲线y=f（x）与直线y=b有两个不同交点，那么b的取值范围是（1，+∞）.

【收获与点评】 （1）在解答本题（2）问时，可转化为判定f（x）=b有两个实根时实数b应满足的条件，并注意g（x）的单调性、奇偶性、最值的灵活应用.另外还可作出函数y=f（x）的大致图像，直观判定曲线交点个数，但应注意严谨性，进行必要的论证.

（2）该类问题的求解，一般利用导数研究函数的单调性、极值等性质，并借助函数图像，根据零点或图像的交点情况，建立含参数的方程（或不等式）组求解，实现形与数的和谐统一.

考点2：导数在不等式中的应用

例2. 已知函数f（x）=ex-ln（x+m）.（1）设x=0是f（x）的极值点，求m，并讨论f（x）的单调性;（2）当m≤2时，证明f（x）>0.

【思维生长点】（1）由极值点确定出实数m的值，然后利用导数求出函数的单调区间;（2）当m≤2时，转化为求f（x）min，证明f（x）min>0.

【收获与点评】 （1）第（2）问证明抓住两点：一是转化为证明当m=2时， f（x）>0;二是依据f ′（x0）=0，准确求f（x）=ex-ln（x+2）的最小值.（2）对于该类问题，可从不等式的结构特点出发，构造函数，借助导数确定函数的性质，借助单调性或最值实现转化.

研究函数的单调性和极（最）值等离不开方程与不等式;反过来方程的根的个数、不等式的证明、不等式恒成立求参数等，又可转化为函数的单调性、极值与最值的问题，利用导数进行研究.

第四单元 定积分与微积分基本定理

【考点聚焦】

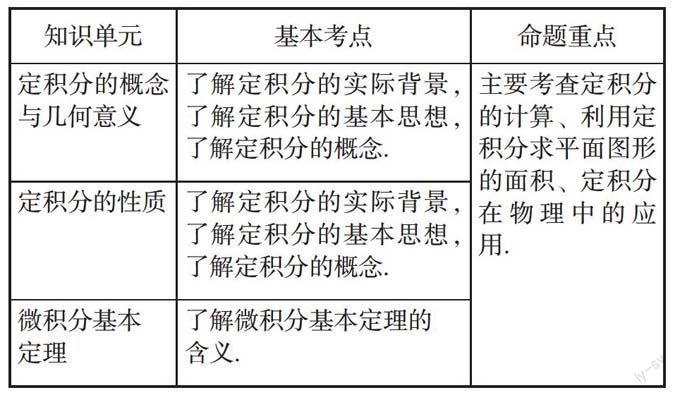
本单元内容主要包括定积分的概念与几何意义、定积分的性质、微积分基本定理.

本单元特别注意：

1. 一种思想：定积分基本思想的核心是“以直代曲”，用“有限”步骤解决“无限”问题，其方法是“分割求近似，求和取极限”.定积分只与积分区间和被积函数有关，与积分变量无关.

2. 一个定理：由微积分基本定理可知求定积分的关键是求导函数的原函数，由此可知，求导与积分是互为逆运算.

3. 两点提醒：一是重视定积分性质在求值中的应用;二是区别定积分与曲边梯形面积间的关系，定积分可正、可负、也可以为0，是曲边梯形面积的代数和，但曲边梯形面积非负.

（作者单位：高慧明：北京市第十二中学;季飞：首都师范大学附属丽泽中学）

责任编校   徐国坚