中学教学中渗透数学模型思想的初探
孙兰香
摘 要:在日常生活中,随时可以用数学知识解决生活中的实际问题的。“数学建模就是把一个具体的实际问题转化为数学问题,然后我们用数学方法解决它,之后我们再把它放回到实际生活当中去,用我们的模型解决现实生活中的种种现象。”
1.在新课教学中注重数学建模
在传统的教育观念下,中学数学教学中学生学习方式主要以接受知识经验为主,忽视自主尝试、探索、建构知识结构,这将影响学生的终身数学发展。数学建模恰恰能改变这种弊端,数学建模注重在数学学习中建立某种数学模型,引导学生发现解决问题的办法,让学生自主探索数学内在的知识与实践应用,利用动手实践、自主探索、合作交流等学习方式开展数学学习活动。例如,“1.2活动思考”一课中,开展搭n个三角形与火柴棒根数的建模活动,教师设计六个层次的搭火柴棒动手实践过程:①搭1个三角形需要火柴棒多少根?②搭2个三角形需要火柴棒多少根?③搭3个三角形需要火柴棒多少根?④搭10个三角形需要火柴棒多少根?⑤搭100个三角形需要火柴棒多少根?⑥搭n个三角形需要火柴棒多少根?学生动手实践,自主探索,发现,第一个三角形需要三根火柴棒,以后每增加一个三角形需要增加两根火柴棒,到搭n个三角形时,需要增加2(n-1)根火柴棒,即搭n个三角形需要火柴棒[3+2(n-1)]根,建构了数学模型,在建模活动过程中学生经历了搭一搭、数一数、归纳等活动,建立了搭n个三角形与火柴棒根数之间的数学关系。在建构过程中,教师有意地引导学生积极思考和主动参与,动手实践,改变以往被动地接受的学习方式,而是让学生的大脑和双手真正动起来。
2.在习题讲解中渗透数学建模
数学模型是通过数学公式、程序、图形、数学符号等对实际问题本质的描绘,它可以解释某些客观现象,也可以预测某些事物的发展规律,还可以为某一事物的发展提供最优的方案和解决方法。数学建模是联系数学与日常生活实际问题的桥梁,可以使复杂的数学问题简单化,在建立数学模型后,所有的问题、事物间的逻辑关系将一目了然,简洁明了。在这些过程中都能促进学生进行“数学的思考”。例如,岁末年终,某甜品店让利促销,请运用本学期所学知识回答下列问题:①若香草口味蛋糕降价10%后的价格恰好比原价的一半多40元,该口味蛋糕原价是多少元?②若同一杯奶茶提供两种优惠:一种是加量30%不加价,另一种是降价30%但是不加量。作为消费者,你认为哪种方式更实惠,为什么?
(1)设该蛋糕原价x元,根据题意得(1-10%)x=—x+40
解得x=100。答:该口味蛋糕原价100元。
(2)设这种奶茶原来售价a元每杯。①第一种方案,相当于每杯价格—=—≈0.77a元;②第二种方案,相当于每杯价格:(1-30%)a=0.7a元
因为0.77x>0.7x,故第二种方式实惠。
对于第①小问,学生只要能建立“降价后的价格=原价的一半+40”这样的模型关系,就很容易解决。对于第②小问,在解决这类问题时,很多学生会无从下手,这就需要教师引导学生通过读题、分析、归纳等思维活动,将本质属性抽取出来,建构一个数学模型。在数学建模活动中,学生发挥想象力、创造力,灵活、合理地选择解决问题的策略。他们独立地思考,从数学建模的角度去探索和研究,并“数学地思考”,通过探索,构造出“现在每杯价格”的数学模型。通过建立数学模型解决该类问题,既可以清楚了解题中所给出的各个条件的作用,又可以将问题中复杂的逻辑关系简单化。
3.在知识运用过程中注重数学建模
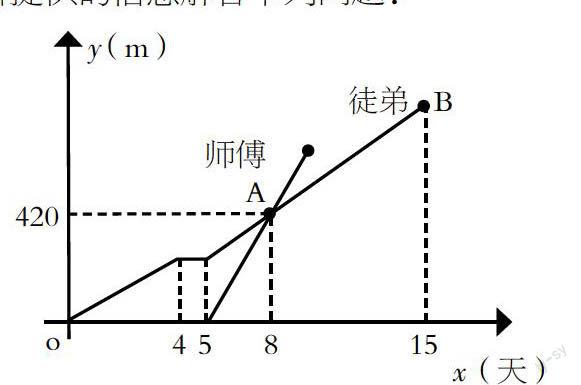
目前很多学生还没有意识到“生活中处处存在着数学,处处存在着要用数学解决的问题”。因此,在我们学完某个知识点的内容之后,教师应利用学生生活中的事情作背景编制数学建模题。这样,既运用了知识,又提高了学生数学的意识以及学习数学的兴趣。例如在学习了函数这一知识点后,我编制了下面的习题:为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒二人合做了5天,师傅被安排做其他的工作,余下的由徒弟单独检修完,下图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象所提供的信息解答下列问题:
(1)点A的实际意义:_________。
(2)求直线AB的函数关系式。
(3)这个自来水管道共有多少?
数学建模让数学知识变无形为有形,从而形成一种更为被学生容易理解的数学结构。我们在教学中有意识地渗透数学建模思想,对培养学生思维品质的灵活性、创造性是十分有益的!
参考文献:
[1]张思明.张思明与数学课题学习[M].北京:北京师范大学出版社,2006.
[2]姜启源,谢金星,叶 俊.数学模型[M].北京:高等教育出版社,2003.
(作者单位:江苏省南京市紫东实验学校)

