线性回归在居民家庭收入与支出中的应用研究
陈智勇

[摘要]线性回归是研究非随机变量与随机变量之间关系的重要方法,线性回归预测是统计学中的重要预测方法。本文以居民家庭收入与支出关系为研究对象,利用线性回归模型,借助Excel工具,给出二者之间的关系,并且对家庭收入在某个特定值时的支出进行预测,以期给相关工作者提供参考。
[关键词]线性回归;居民收入;居民支出
[DOI]10.13939/j.cnki.zgsc.2015.13.012
1线性回归模型简介
简单地说,回归分析是通过建立回归模型研究相关变量之间的关系并做出相应的估计和预测的统计方法。一元线性回归是最简单的回归分析,其基本步骤是这样的。
第一步,建立模型。首先应当利用专业知识或者散点图判断y与x是否存在呈线性相关关系,其中y是被解释变量,也是随机变量;x是解释变量,也是非随机变量。若二者之间存在线性相关关系,y与x之间的关系可表达为y=β0+β1x+ε,这里β0是截距,β1是斜率,二者统称为回归系数,ε是随机扰动项。解释变量x与随机扰动项ε共同导致了随机变量y离开均值产生变化。
第二步,估计回归系数。一般我们采用最小二乘法来计算0和1。我们用直线=0+1x去拟合{xi,yi}(1≤i≤n)这些散点,我们自然要求拟合偏差的平方和Q=ni=1(yi-i)2最小,即Q=ni=1(yi-0+1xi)2最小。Q是0和1的函数,令其对0和1的偏导数为0,可以计算出0和1。引入记号Sxx=ni=1(xi-)2, Sxy=ni=1(xi-)(yi-), Syy=ni=1(yi-)2, 则有公式:
1=SxySxx
0=-1
第三步,回归方程的显著性检验。
检验方程的显著性,我们只需检验β1是否为0。作假设H0∶β1=0。对于给定的显著性水平α,由于α=P{F>Fα(1,n-2)},若F>Fα(1,n-2),即F只有α的可能性大于Fα(1,n-2),而现在确实大于了,所以我们拒绝H0,认为回归方程显著,否则认为回归方程不显著。这种方法F称为检验法。
第四步,利用方程进行预测。若回归方程经过检验是显著的,那么可以将变量取值代入回归方程求出因变量的预测值。
2线性回归模型在居民家庭收入与支出中的应用
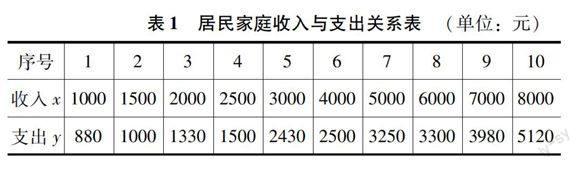
家庭收入与消费的线性回归:某地区家庭收入与家庭消费支出的调查数据如表1所示。建立家庭收入和家庭消费支出之间的线性回归模型,并预测家庭收入为9000元时的家庭消费支出。
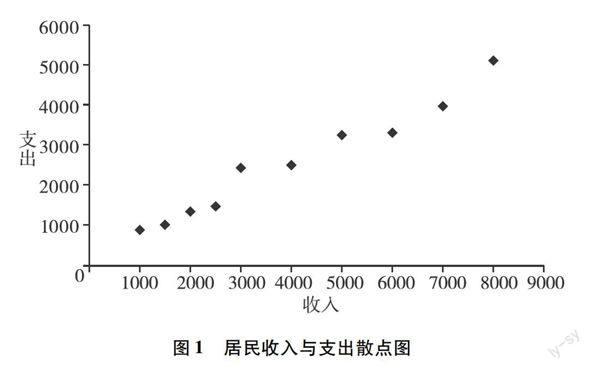
我们观察散点图1,可知居民收入与支出呈线性相关关系。
下面,我们按照一元线性回归的4个步骤来建立回归方程,预测家庭收入为9000元时的消费支出。
第一步,设支出为y,收入为x,并且二者之间存在线性相关关系,即有y=β0+β1x+ε。其中β0是截距,β1是斜率,统称回归系数,ε是随机扰动项。收入x与随机扰动项ε共同导致了随机变量y离开均值产生变化。
第二步,估计回归系数。我们当然可以第一部分的公式1进行计算,但是其较为烦琐。我们可以利用统计软件Excel计算其回归系数。我们在Excel2010中依次点击“文件”——“选项”——“加载项”——“分析工具库”——“转到”——“分析工具库”——“确定”可以加载“数据分析工具”。现在,我们可以使用Excel2010的“数据分析工具”进行回归分析了。由于Excel只能识别纵向数据,所以应当先将数据由“横向”转化为“纵向”,使用Excel的“选择性粘贴”即可实现。
我们点击Excel2010的“数据”选项卡,再点击“数据分析”按钮,这时会出现一个对话框,问你选择何种分析工具,我们选择“回归”。之后,我们根据要求填写“Y值输入区域”、“X值输入区域”(这两项也可以用折叠按钮点选),选择“置信度”为95%,选择“输出区域”为新工作表,勾选线性拟合图,即可得到回归系数的估计值等一系列的结果。回归系数的估计值的结果如表2所示。
表2中Coefficients意思是“系数”,Intercept意思是“截距”,Variable意思是“变量”,表2表明x前的系数为259,截距为0.56,回归方程为:y=0.56x+259;
我们可以画出收入、支出拟合图,由图2可以看出拟合效果非常好。
第三步,回归方程的显著性检验。上述拟合效果只是直观感受,方程的显著性需要进一步的检验。我们检验方程的显著性,只需检验β1是否为0。现在我们显著性水平取为0.05,查 分布上侧分位数表得Fa(1,8)=5.32。我们用Excel2010的“数据分析工具”得出该线性回归方程的值为227.47。也就是说,在显著性水平为0.05下,拒绝假设,回归方程显著。
第四步,利用回归方程进行预测。上面已经证明了回归方程在显著性水平为0.05下是显著的,此时,我们可以利用回归方程进行预测当家庭收入为9000元时,家庭消费支出的预测值。将11代入线性回归方程中的x,即可得出11等于5299元。
3结论
本文介绍了一元线性回归的基本理论,包括概念引入、建立模型、举例分析和预测等。线性回归是生产运作中常用的预测方法。为提高使用效率本文使用Excel软件对一元线性回归进行分析预测,求解了家庭居民收入与支出之间的相关关系,并且给出了当家庭收入为9000元时的支出预测值,圆满地完成了本文的任务。
参考文献:
[1]费宇.应用数理统计——基本概念与方法[M].北京:科学出版社,2007.
[2]陈希孺.概率论与数理统计[M].合肥:中国科学技术大学出版社,2011.
[3]崔鹏,高松,张丽.线性回归在居民家庭收入与支出中的应用[J].商,2013(23).
[4]齐峰,徐丽丽.关于农民人均收入预测的线性回归模型[J].科学教研,2013(11).
[5]陈肯界.现金流通与物价指数的实证研究[J].中国市场,2014(44).
[6]贺铿.中国经济发展的影响因素与关注点[J].中国市场, 2014(11).
[7]王桃桃.城镇化对我国城乡收入差距的影响[J].中国市场, 2014(42).

