怎样培养学生的创造思维能力

布音塔

一、 指导观察

观察是信息输入的通道， 是思维探索的大门. 敏锐的观察力是创造思维的起步器. 可以说， 没有观察就没有发现， 更不能有创造.  儿童的观察能力是在学习过程中实现的， 在课堂中， 怎样培养学生的观察力呢？首先， 在观察之前， 要给学生提出明确而又具体的目的、任务和要求. 其次， 要在观察中及时指导.  比如要指导学生根据观察的对象有顺序地进行观察， 要指导学生选择适当的观察方法， 要指导学生及时地对观察的结果进行分析总结等. 第三， 要科学地运用直观教具及现代教学技术， 以支持学生对研究的问题做仔細、深入的观察.  第四， 要努力培养学生浓厚的观察兴趣. 如学习《三角形的认识》， 学生对“围成的”理解有困难. 教师可让学生准备10厘米、16厘米、8厘米、6厘米的小棍各一根， 选择其中三根摆成一个三角形. 在拼摆中， 学生发现用10、16、8厘米， 10、8、6厘米和10、16、6厘米都能拼成三角形， 当选16厘米、8厘米、6厘米长的三根小棒时， 首尾不能相接， 不能拼成三角形. 借助图形， 学生不但直观的感知了“三角形两边之和不能小于第三边”， 而且明白了“三角形”不是由“三条线段组成”的图形， 而应该是由“三条线段围成”的图形， 使学生对三角形的定义有了清晰的认识. 因此， 在概念的形成中教师要努力创造条件， 给学生提供自主探索的机会和充分的思考空间， 让学生在观察、操作、实验、归纳和分析的过程中亲自经历概念的形成和发展过程， 进行数学的再发现、再创造.

二、 引导想象

想象是思维探索的翅膀. 爱因斯坦说：“想象比知识重要， 因为知识是有限的， 而想象可以包罗整个宇宙. ”在教学中， 引导学生进行数学想象， 往往能缩短解决问题的时间， 获得数学发现的机会， 锻炼数学思维. 想象不同于胡思乱想. 数学想象一般有以下几个基本要素. 第一， 因为想象往往是一种知识飞跃性的联结，因此要有扎实的基础知识和丰富的经验的支持. 第二， 是要有能迅速摆脱表象干扰的敏锐的洞察力和丰富的想象力. 第三， 要有执着追求的情感.  因此， 培养学生的想象力， 首先要使学生学好有关的基础知识. 其次， 新知识的产生除去推理外， 常常包含前人的想象因素， 因此在教学中应根据教材潜在的因素， 创设想象情境， 提供想象材料， 诱发学生的创造性想象. 如在学习《平行四边形的面积》时， 教师利用多媒体呈现学生熟悉的情景： 种植园里各种植物郁郁葱葱，分别种在划成不同形状的地块上. 然后出示种有竹子和杜鹃的地块， 分别呈正方形和长方形， 要求算一算他们的种植面积， 学生运用已学的知识很快解决了问题. 接着出示一块形如平行四边形的青菜地， 让学生猜一猜它的面积大概是多少？平行四边形的面积应怎么求？学生对未知领域的探索有天然的好奇， 思维的积极性被激发， 纷纷根据前面的知识作出如下猜测： ①、面积是长边和短边长度的积. ②、长边和它的高的积. ③、短边和它的高的积. ④、先拼成一个长方形， 跟这个长方形的面积有关……教师一一板书出来， 学生见自己的思维结果被肯定， 心理上有一种小小的成就， 从而更激起了主动探索的欲望.

三、 鼓励求异

求异思维是创造思维发展的基础. 它具有流畅性、变通性和创造性的特征.  求异思维是指从不同角度， 不同方向， 去想别人没有想到， 去找别人没有找到的方法和窍门. 要求异必须富有联想， 好于假设、怀疑、幻想， 追求尽可能新， 尽可能独特， 即与众不同的思路. 课堂教学要鼓励学生去大胆尝试， 勇于求异， 激发学生创新欲望.

学起于思， 思源于疑， 疑则诱发创新. 教师要创设求异的情境， 鼓励学生多思、多问、多变， 训练学生勇于质疑， 在探索和求异中有所发现和创新. 本人教授“§2.7 平行线的性质”一节时深有感触， 一道例题最初是这样设计的：

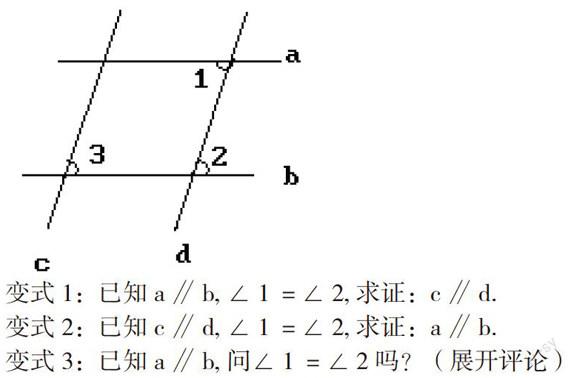
例：如图，已知a∥b， c∥d， ∠1=115°，

（1） 求∠2与∠3的度数，

（2）从计算你能得到∠1与∠2是什么关系？

学生很快得出答案， 并得到∠1=∠2. 我正要向下讲解， 这时一位学生举手发言：“老师， 不用知道∠1=115°也能得出∠1=∠2. ”我当时非常高兴， 因为他回答了我正要讲而未讲的问题， 我让他讲述了推理的过程， 学生们报以热烈的掌声. 我又借题发挥，随之改为： 已知a∥b， c∥d求证：∠1=∠2让学生写出证明， 并回答各自不同的证法. 随后又变化如下：

变式1：已知a∥b， ∠1=∠2，求证：c∥d.

变式2：已知c∥d， ∠1=∠2，求证：a∥b.

变式3：已知a∥b， 问∠1=∠2吗？（展开评论）

这样， 通过一题多证和一题多变， 拓展了思维空间， 培养学生的创造性思维.  对初学几何者来说， 有利于培养他们学习几何的浓厚兴趣和创新精神. 数学教学中， 发展创造性思维能力是能力培养的核心， 而逆向思维、发散思维和求异思维是创新学习所必备的思维能力. 数学教学要让学生逐步树立创新意识， 独立思考， 这应成为我们以后教与学的着力点.

四、 诱发灵感

灵感是一种直觉思维. 他大体是指由于长期实践， 不断积累经验和知识而突然产生的富有创造性的思路. 它是认识上质的飞跃. 灵感的发生往往伴随着突破和创新.

在教学中， 教师应及时捕捉和诱发学生学习中出现的灵感， 对于学生别出心裁的想法， 违反常规的解答， 标新立异的构思， 哪怕只有一点点的新意， 都应及时给予肯定. 同时， 还应当运用数形结合、变换角度、类比形式等方法去诱导学生的数学直觉和灵感， 促使学生能直接越过逻辑推理而寻找到解决问题的突破口.

例如， 有这样的一道题： 把3/7、6/13、4/9、12/25用“>”号排列起来. 对于这道题， 学生通常都是采用先通分再比较的方法， 但由于公分母太大， 解答非常麻烦. 为此， 我在教学中， 安排学生回头观察后桌同学抄的题目（7/3、13/6、9/4、25/12）， 然后再想一想可以怎样比较这些数的大小， 倒过来的数字诱发了学生瞬间的灵感， 使很多学生寻找到把这些分数化成同分子分数在比较大小的简捷方法.

总之， 人贵在创造， 创造思维是创造力的核心. 学生的创造思维能力如何培养如何提高是学校教学工作新的难题， 培养有创新意识和创造才能的人才是中华民族振兴的需要， 让我们共同从课堂做起.