调相和调幅调相信号基于高阶累积量的识别方法
贺辉刚 文方 蒋宗明
【摘要】 针对当前电子战侦察中调相信号如BPSK、QPSK与调幅调相信号如16QAM在调制识别时存在识别困难的问题,本文提出了基于高阶累积量的数字信号调制识别方法,可以将调相信号与调幅调相信号区别开来,从理论上分析该方法的可行性并通过MATLAB进行仿真验证了算法的有效性。
【关键词】 调制识别 高阶累积量 16QAM QPSK
一、引言
调制样式识别是通信电子战的重要内容之一,它为解调器正确选择解调算法并进一步获取敌方通信信息提供参数依据,同时还可以引导干扰设备采用最佳的干扰模式对敌方通信链路进行干扰,从而造成其指挥、控制等信息传递不畅[1]。
由于BPSK、QPSK、16QAM等信号功率谱利用率高,它们得到了广泛的应用。因此对BPSK、QPSK、16QAM这几种调制信号的识别有十分重要的意义。
数字信号调制识别目前最为常用的方法是通过计算信号的二阶统计量(相关函数或者功率谱),但是相关函数和功率谱又存在它们不能辨识非最小相位系统的缺点,另外二阶统计两对加性噪声很敏感,所以能够处理的信号类型也很有限。
基于高阶累积量特征的调制样式识别方法是近几年来提出的统计模式识别方法,由于高斯白噪声的三阶及以上累积量为零,因此它有很好的信噪比适应能力,能有效地消除载波频率偏移、相位抖动,在工程上有很高的使用价值[4]。
二、高阶累积量算法
高阶累积量是描述随机过程高阶统计特性的一种数学工具,自1990年以来,得到了迅速的发展,成为现代信号处理的重要工具之一。
对于一个具有零均值的复随机过程X(k),其p阶混合矩可以表示为[4]:
Mpq=E(X(k)p-qX*(k)q) 式(2.1)
其中,*表示信号的共轭分量,在这个基础上我们定义高阶累积量如下[4]:
假设发送的信号序列是独立同分布的,根据式(2.1)式(2.1)~(2.8)进行计算之后得到BPSK、QPSK和16QAM信号的各阶累积量的期望值如表1和表2:
三、调相信号和调幅调相信号基于高阶累积量的调制识别方法
本文采用的待识别信号的调制样本为{ BPSK、QPSK、16QAM},输入信号样本为接收信号的同步复信号序列。
对于BPSK信号和16QAM信号,令Fx1=|C20|/|C21|。理论上BPSK、QPSK、16QAM信号Fx1的值为分别为1、0、0。通过比较Fx1可以区分出BPSK和QPSK、16QAM信号。
若要区分QPSK和16QAM信号,由表一可知,一般通过比较QPSK和16QAM信号的6阶累积量|C63|来区分这两种信号。若令QPSK和16QAM信号的振幅E均为1,那么对于QPSK和16QAM信号,它们的Fx2的值分别为4和0.28 。在信噪比SNR=10时,QPSK信号识别率达到52.5%,16QAM信号的识别率为32.5%[8];SNR=20时,QPSK信号的识别率达到94.5%,16QAM信号的识别率为89.5%[8]。
由式(2.2)~(2.8)可知信号的n阶累积量和信号的n阶矩以及n-2阶矩有关,高阶累积量计算量的增加也会带来识别误差的增加,实际工程中也会由于计算量增加达不到实时调制信号识别的效果。因而减小计算量成为了提高高阶累积量调制识别方法的识别效率的有效途径。根据表1取Fx2=|C40|/C212,可知对于QPSK和16QAM信号的理论值分别为1和0.68。这样只计算信号的四阶累积量,就实现了QPSK16QAM信号的调制样式识别。
故而本文提出了基于高阶累积量识别BPSK、QPSK、16QAM信号的流程图如图1。
四、算法仿真及结果
实验中信道为高斯白噪声信道,假设接收机已经完成了载波,相位和定时均同步。调制信号载波频率为150 kHz, 码元速率为25kHz, 采样频率为1200 kHz, 采样点N= 4096。
4.1 BPSK与QPSK、16QAM信号的调制识别
按照图1的识别流程图,在MATLAB平台下仿真对BPSK、QPSK、16QAM三种信号进行高阶累积量计算的二阶计算500次,得到各个信号在不同信噪比下Fx1的值的曲线如图2。
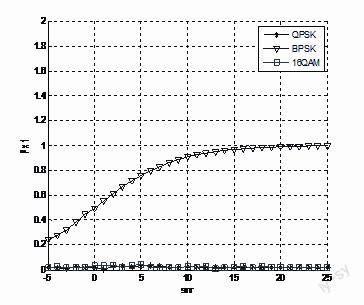
由图2可以看出随着信噪比的增加,BPSK信号的Fx1的值趋近于理论值1,而16QAM信号和QPSK信号的Fx1的值趋近于理论值0。在信噪比超过10dB的条件下,通过对比Fx1的值可以很好的区分出BPSK信号和QPSK、16QAM信号,但是不能区分出QPSK和16QAM信号。
4.2 QPSK信号与16QAM信号的调制识别
按照图1的识别流程图,在MATLAB平台下仿真对QPSK、16QAM信号进行高阶累积量计算的四阶计算500次,得到它们在不同信噪比下Fx2的值的曲线如图3。
由图3可以看出,随着信噪比的增加,QPSK信号的Fx3的值趋近于理论值1,而16QAM信号的Fx3的值趋近于理论值0.68。在信噪比超过10dB的条件下,通过对比Fx3的值可以很好的区分出QPSK信号和16QAM信号。
五、结论
本文提出的改进的基于高阶累积量的数字调制识别方法,在MATLAB平台下可以在信噪比高于10dB时,对BPSK、QPSK、16QAM信号有很好的识别效果,解决了运用高阶累积量对16QAM信号与QPSK信号调制识别需要计算6阶累积量,计算量大并且识别效果不好的问题。通过在MATLAB平台实验仿真结果来看,本文所提出的方法对实际工程中调相信号(MPSK)与调幅调相信号(MQAM)信号的调制识别有重要的参考意义。
参 考 文 献
[1]罗利春.无线电侦察信号分析与处理[M].北京:国防工业出版社,2003.
[2]王秉钧,王少勇,田宝玉.现代卫星通信系统[M].北京:电子工业出版社, 2004.
[3]皇埔堪,陈建文,楼生强.现代数字信号处理[M].北京:电子工业出版社,2003.
[4]杨杰,孙钢灿,通信信号调制识别:原理与算法[M].北京:人民邮电出版社,2014.
[5]Pedzisz M, Mansour A. Automatic modulation recognition of MPSK signals using constellation rotation and its 4th order cumulant[J].IEEE Trans.on Signal Processing, 2005, 15:295-304.
[6]Dobre O A, Bar-Ness Y, Su W. Higher-order cyclic cumulants for high ordermodulation classification[J].Proc. IEEE Milcom, 2003: 112-117.
[7]吕新正,魏平.利用高阶累积量实现数字调制信号的自动识别[C].中国通信学会第五届学术年会论文集,2008
[8]成静,李钢虎,周关林.高阶累积量计算优化的仿真研究[J].计算机仿真,2009,26(8):80-83
[9]郭龙,邱天爽.无线通信信号的调制识别研究[D].大连理工大学.2010,6
[10]李静克.无线通信调制方式的自动识别算法研究[D].西南交通大学.2011.6

