浅谈初中数学教学思想的运用
李远信

数学思想是人们在认识数学、研究数学的过程中不断地对数学的内容、本质理解所形成的认识. 所谓万变不离其宗,数学思想最重要的特性就是将遇到的问题抽丝剥茧,直至找到问题的根源,揭示其中的原理、本质. 数学思想是人们利用数学最有效的方法,学习数学亦是如此,掌握好最重要的一些数学思想,将有助于解开一道道难题. 常用的数学思想大致可以分为:函数方程、数形结合、分类讨论、转化与归类.
1. 函数方程思想
函数方程思想是指通过探索某两种变化量之间的联系,建立起数学模型,利用方程的形式解决问题.
例如:某中学为了鼓励学生,准备给每位优秀学生奖励一支钢笔和一个笔记本. 学校安排李老师去采购,一共有20名优秀学生,已知钢笔单价是笔记本单价的2倍,而李老师一共花去了300元,请问钢笔和笔记本的单价各是多少?
可以这么解题:设笔记本的单价为x,那么钢笔的单价为2x. 则可以得到一个关系等式:(2x + x)20 = 300,由此可以算出x = 5,即笔记本的单价为5元,钢笔的单价为10元.
这是一个简单的例子,函数方程思想可以将许多生活中的问题转化为数学问题,通过函数、方程这样的数学语言来解决问题.
2. 数形结合思想
数学离不开一个个复杂的公式,也离不开一个个抽象的字符. 数形结合思想特质就是可以把数学从这种抽象的形式转化为直观的图形,从而达到两者相互结合的效果.
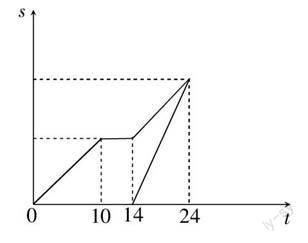
例如:暑假里早上爸爸带着鹏鹏去跑步,爸爸起得早先跑了10分钟,打了个电话让鹏鹏出门,爸爸在休息了4分钟之后又继续跑步,与此同时鹏鹏也正好从家出发,10分钟之后二人相遇,假设爸爸跟鹏鹏所走途径相同,问爸爸与鹏鹏的速度之比为多少?
解析 我们可以将题中二人所走的过程绘成如上图所示,通过上图我们可以很直观地看到两者的时间跟距离之间的关系,v1 × 10 + 0 × 4 + v1 × 10 = v2 × 10,可得v1 ∶ v2 = 1 ∶ 2,即爸爸与鹏鹏的速度之比为1 ∶ 2.
数学问题有很多看似很复杂的东西,只要通过数形结合的思想巧妙地变化一下,就会有种茅塞顿开的感觉,思路一下子会清晰很多.
3. 分类讨论思想
在解决数学问题时,时常会遇到很多情况,需要逐个进行分析讨论,最终将所有情况综合,这就是数学中重要的分类讨论思想. 分类讨论值得注意的地方是:首先要考量分类的大范围;其次分类的过程一定要思路清晰、主次分明,不能重复或遗漏. 不同分类的对象,只要能做到上述所说,产生的结果是一样的. 举个例子:在学习一次函数的时候,在直角坐标系中,分别以x方向和y方向作为对象,讨论的结果一定是一样的,因为每一个x的值都相对应一个y的值,反过来也是如此.
4. 转化与归类思想
转化与归类思想又称等价转化,其目的是将数学中复杂的问题通过一系列方法转化为熟悉的、简单的、在已知知识范围内的问题. 这种思想较为灵活,需要一定应变能力,也时常成为一些解题的精妙之处.
例如:计算
解析:
以上相加可得
转化与归类思想的巧妙运用经常会给数学添加许多乐趣和魅力,这也是数学神奇的地方之一.
总结:新课改以来,我们现在的教学更倾向于培养学生的数学思想,目的也是为了让学生掌握最基本的解题技能,“授之以鱼,不如授之以渔”说的就是这个道理. 我们教师在教学过程中,根据教程内容渗透性地将这些基本的数学思想灌输给学生.

