初中数学解题小结指导

陈吉标

摘 要：数学解题小结指学生解题后对题型特征、问题内涵、思维陷阱、解题方法等有关内容进行分析与梳理的学习活动.引导学生进行解题小结，作为一种学习方法指导，它既是贯彻“教会学生学会学习并掌握学习”的课程教育理念的有效方式，又是大幅度提高课程学习质量的重要手段.

关键词：解题小结；题型归类；辨识题结；拓展变换；方法梳理

课程教学的育人功效是促进学生思想的形成、情感的孕育、思维的发展、能力的提升等，而教会学生解决与课程知识有关的实际问题则是课程教学的基准点 [1 ].换句话说，课程教学必须教会学生解题.这不仅因为考试成绩决定着学生的学业前途，更重要的是通过考察学生的解题来评价课程教学在知识与技能目标方面的落实程度.

数学解题小结是指学生解题后对题型特征、问题内涵、思维陷阱、解题方法等有关内容进行分析与梳理的学习活动.本文就初中数学课程教学如何指导学生开展解题小结，谈谈个人的实践与认识.

1 题型特征归类

题型特征，指题目在知识的适用范畴或数学方法运用等方面有着显性或潜在的特点.如题目“已知A=a4-2a2+1，B=-3a4-4a2+2，计算3A-B”， 就知识的适用范畴来说，其特征就是代数多项式的加减运算.就运算方法而言，其特征就是“合并同类项”.

按题目的构成背景，数学题目大致可以分为两大类，第一类是数学知识问题，用于直接考查学生对数学知识与方法的运用能力.第二类是数学应用问题，即数学知识在实际生活中的应用问题.

在数学课程学习中，学生所形成的知识结构中数学符号或图形为主要结构元素.如有关一元二次方程的知识结构：方程的一般化形式为ax2+bx+c=0（a≠0），对于解方程方法，如果b=0，采用开平方方法，如果c=0，采用分解因式方法，如果b、c均不等于0，一般用公式法，即x=■.虽然学生对数学知识具有这样的建构特点的认知，似乎有助于辨识第一类数学题的特征，但是由于问题形式的变化，要迅速准确的判定每题的知识适用范畴或方法运用还须经历一个分析与归类的解题反思过程.如题目“已知2+■是方程x2-4x+c=0的一个根，求方程的另一个根及c的值”，它似乎属于解一元二次方程，但其中又牵涉到“两数和的平方展开、代数多项式加减、解一元一次方程”等有关问题，如果没有经历其实际解题过程且进行解题后的小结，学生就难以认识本题的综合特征.

题型特征归类的重点在于第二类问题.这类问题的构成背景是实际生活，有的问题会给出某种数学知识模型，有的则没有.如题目“一个直角三角形的斜边长7cm，一条直角边比另一条直角边长1cm，求两条直角边的长度”，它属于什么知识或运用什么方法的问题，只有经过解题并反思的思维活动方能明确.

对于题型特征归类，不仅要分析当前所做的题目，还要分析与当前类似的问题，既要寻找它们的共同点，又要辨识它们的不同点.如2（x+3）2=x（x+3）与（x+1）2-3（x+1）+2=0，共同的解法是先转化为一元二次方程的标准形式再解方程，不同点是后者可以化为y2-3y+2=0，前者则不能.

2 辨识题眼题结

“题眼”指题目文字中的关键词或体现某种数学特征的文句.如题目：一件夹克衫按成本价提高50%后标价，后因季节关系按标价的8折出售，每件以60元卖出，这批夹克每件的成本价是多少元？其中“成本价”就是本题关键词，假设成本价为x元，出售标价就是x+50%x元，卖出价则是（x+50%x）×0.8元.显然，在本题有关的问题分析中，都与“成本价”有关.再如题目：某汽车在公路上行驶，它行驶的路程s（m）和时间t（s）之间的关系为s=10t+3t2 ，那么行驶200m需要多长时间？其中 “它行驶的路程s（m）和时间t（s）之间的关系为s=10t+3t2”的文句就是“题眼”，它表征本题属于解一元二次方程的应用问题.

所谓“题结”，指解答题目的困惑或障碍所在.“题结”往往体现为方法或技巧问题，如几何证明题的补作辅助线，代数问题中数学形式的巧妙转换等.认识“题结”，往往表现在分析题意后突然会觉得“束手无策”.解开“题结”，就思维过程而言，就是指思维方向的突破或思维角度的变换.如题目：一次会议上，每两个参加会议的人都互相握了一次手，有人统计一共握了66次手，这次到会的人数是多少？“互相握手”是本题的“题眼”，本题应从互相握手的特点来分析.假设到会人数为x，那么第一个人与其他人握手的次数为（x-1）次，第二、三……等每个人的握手次数分别为（x-2），（x-3）……（x-x+1）次，总次数为66=（x-1）+（x-2）+（x-3）……+（x-x+1）.

本题的“题结”就是右边多项式的合并运算.它牵涉到的方法或技能就是将右边多项式之和转化为某种确定的代数形式.如果认真分析，右边多项式为1+2+3+……（x-1），它属于连续自然数之和，依据连续自然数之和的计算公式■，则前面等式可以写为■=66，显然，它是解一元二次方程的问题.

辨识“题眼”有助于提升学生的读题与审题能力，较好地把握题目的内涵，从而能迅速地将当前问题纳入自己原有的知识与方法体系结构并形成正确地解题思路或方法.辨识“题结”有助于促进学生在解题方面的类化能力，如体育项目的循环赛场数统计、班级学生座位安排形式统计等蕴含组合性质的问题，都可以类化为“互相握手”问题来解决.

3 问题拓展变换

引导学生开展解题小结的思维活动目的在于促进学生达到“做一题通一类”的解题效果.应该说，对于某一数学问题模型，它所牵涉到的知识与方法内容，大体上是确定的，但它却可以从不同的角度来设计不同的问题.如下面题目：

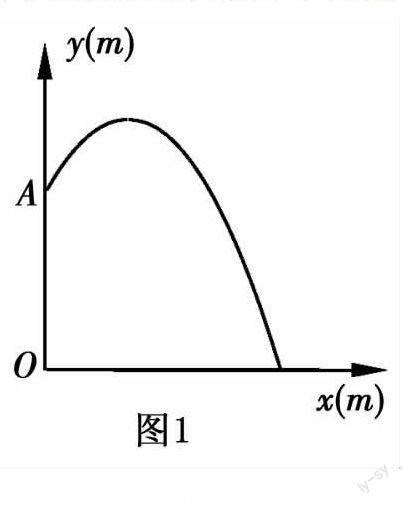
如图1所示，一个圆形喷水池的中央竖直安装了一个柱形装置OA，A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线喷出的高度y（m）与水平距离x（m）之间的关系式是y=-x2+2x+■（x>0），柱子OA的高度为多少米？若不计其它因素，水池的半径为多少米，才能使喷出的水流不至于落在池外？

本题属于二次函数知识与图像方法在生活中的应用，所牵涉到的知识主要有y=ax2+bx+c顶点坐标、图像的开口方向、求图像与坐标轴的交点等.就这个生活背景问题，它可以从如下不同角度来设计问题：

（1）原题设计思路：给出具体的函数形式，求图像与x、y轴的交点坐标；

（2）变换设计思路①：给出具体的函数形式，求水柱最高点所形成的半径；

（3）变换设计思路②：给出柱子OA高度值与图像与x轴的交点坐标值，求抛物线的函数表达式；

（4）变换设计思路③：给出抛物线的顶点坐标值与柱子OA的高度值，求抛物线的函数表达式；

（5）变换设计思路④：给出喷头高度值和喷头与图像在x轴交点的距离值，求水柱最高点所形成的半径.

对于命题者，他可以从不同角度来设计问题，然而对于做题者，他也可以从不同的角度来拓展或变换原题的问题情境.做题者对原题的拓展与变换过程，实质上是将已构建的概念性知识与方法再次具体化，以致形成更丰富且更深刻的认知结构.因此，引导学生对原题尝试拓展变换并构建相应的解题思路，不仅可以促进学生深刻把握原题的内涵，而且还可以促进学生贯通原题中牵涉到的数学知识与方法，从而收到“做一题通一类”的解题效益.当然，就初中学生，针对原题进行拓展变换，在思维方面，初始阶段会呈现为能力欠缺，但随着训练次数的增加，这种能力就会逐步提升，一旦形成了这种能力与习惯，那就达到了掌握学习方法的较高层次.

4 解题方法梳理

解题方法梳理，就是指归纳或总结某类题型的解题思路与方法.问题拓展变换的思维活动为题型类化提供了丰富的素材，如果说拓展变换是“做一题通一类”的“发酵”过程，那么解题方法梳理则是形成解题能力的“提炼”过程.没有“发酵”，何有“提炼”，前者是后者的具体化，后者是前者的概括化.从思维活动特征而言，前者是以知识内涵为出发点，而后者则是以技能方法为落脚点，知识转化为能力就是在这两个过程中得以实现.

解题方法梳理，首先是分别列出原题和拓展变换后问题的解题思路或方法.如上面列举的“喷水池”问题：

原题：求OA高度，令x=0，由函数求y值；求水池半径，令y=0，解一元二次方程；

变换①：求水柱最高点所形成的半径，依据顶点坐标公式计算；

变换②：设交点式函数y=（x-x1）（x-x2），代入A和图像与x轴交点坐标值，解方程组；

变换③：设顶点式函数y=a（x-k）2+h， 代入顶点坐标值与A点高度值，解方程组；

变换④：依据直角三角形边长关系求出图像与x轴交点坐标值，应用变换②的解题方法.

其次是归纳或梳理关于解答二次函数问题的通用方法.对于上面问题的思路与方法，它可以归纳为以下通用思路或方法：

（1）已知函数而求图像与两坐标轴的交点：令x=0或令y=0，解函数方程；

（2）已知函数而求抛物线的顶点，依据顶点坐标公式求解；

（3）已知图像中的某两点坐标求函数形式，设交点式函数y=（x-x1）（x-x2），代入两坐标值后解方程；

（4）已知图像顶点坐标求函数形式，设顶点式函数y=a（x-k）2+h，再结合有关条件求解.

通过这种归纳，学生基本上掌握了解决二次函数问题的基本思路与方法.显然，它与前面的拓展变换的思维活动有关.其中内容越丰富，归纳就越全面，对知识与方法的建构就越深刻，解题能力就越强.不难看出，上面未归纳出一般式y=ax2+bx+c的应用情形就是一种欠缺.可见，引导学生开展对问题的拓展变换是数学解题指导中的重头戏.

引导学生进行解题小结，作为一种学习方法指导，它既是贯彻“教会学生学会学习并掌握学习”的课程教育理念的有效方式，又是大面积提高课程学习质量的重要手段.

参考文献：

[1] 崔允漷，有效教学[M].上海：华东师范大学出版社，2009.