参数假设检验中的两类错误

沈荣泸

【摘要】本文在正态总体的总体均值右侧假设检验前提下，对假设检验的两类错误进行探讨，进而得出犯两种错误的概率α和β的关系式，最后在得到的关系式下形成三点结论.

【关键词】假设检验；小概率原理；抽样分布；弃真错误；纳伪错误

参数假设检验是根据总体的理论分布和小概率原理，对未知或不完全知道的总体提出两种彼此对立的假设，然后由样本的实际结果，借助相应的抽样分布，经过一定的计算，对两种彼此对立的假设在一定概率前提下作出推断.下面针对总体未知参数均值μ进行展开.

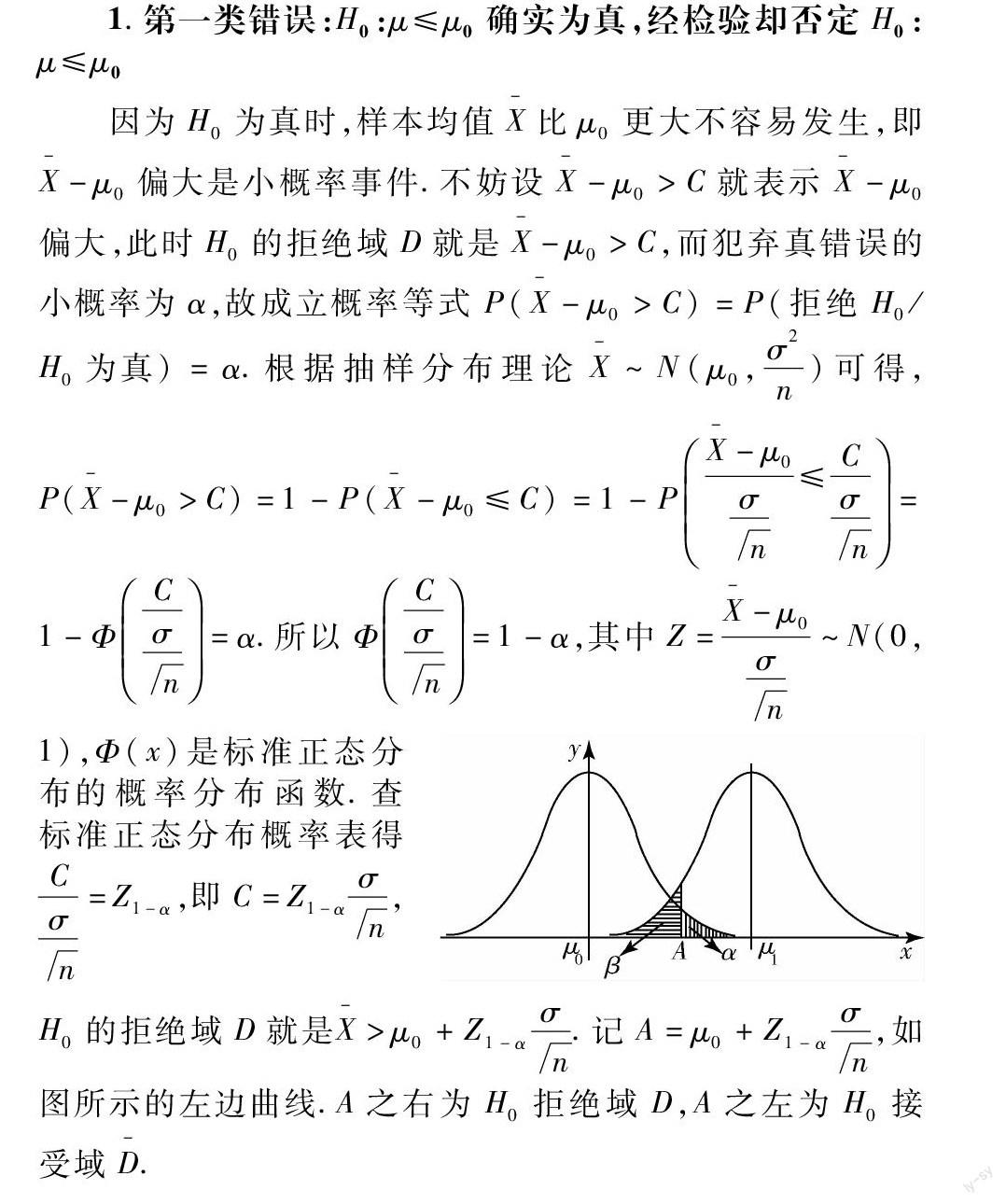
参数假设检验中相互对立的两种假设通常称为原假设H0和备择假设H1，由于是利用样本信息对总体参数进行推断，所以有可能犯以下两类错误：第一类错误，也叫弃真错误，当原假设H0确实为真时，而样本统计量的值却落入拒绝域D内，从而作出否定H0的推断，若将犯第一类错误的概率记为α（通常称为显著性水平或检验水平），则满足概率等式P（拒绝H0/H0为真）=α；第二类错误，也叫纳伪错误，当原假设H0确实为假，即H1为真时，而样本统计量的值却落入接受域D-内，从而接受H0，若将犯第二类错误的概率记为β，此时满足概率等式P（接受H0/H0为假）=β或P（接受H0/H1为真）=β；为了便于说明，我们用正态总体X～N（μ，σ2）下，方差σ2已知，對总体均值μ的右侧检验来进行说明.此时原假设为H0：μ≤μ0；备择假设为H1：μ=μ1>μ0.从总体X中抽取样本容量为n的简单随机样本，其样本均值为X-.