基于非线性灰色微分方程的PPI预测

查进道

摘 要：由于工业品出厂价格指数（PPI）是衡量工业产品出厂价格变动程度的指数，PPI的变化会影响居民消费价格指数（CPI），存在PPI向CPI的传导关系，是有关部门制定经济政策的重要依据，因而对PPI进行有效的预测具有现实的重要意义。由于微分进化算法（DE）具有很强的全局寻优功能、较快的收敛速度及较好的稳定性的优点，该文采用微分进化算法对非线性灰色微分方程中的参数进行寻优，从而建立起基于非线性灰色微分方程的PPI预测模型，仿真结果表明了该模型的有效性。

关键词：工业品出厂价格指数 非线性灰色微分方程 微分进化算法 基于非线性灰色微分方程的PPI预测模型

中图分类号：TP18 文献标识码：A 文章编号：1672-3791（2015）09（a）-0095-02

工业品出厂价格指数（PPI）是衡量工业产品出厂价格变动程度的指数，它反映了生产领域价格的变动情况， PPI的变化会影响居民消费价格指数（CPI），存在PPI向CPI的传导关系，是有关部门制定经济政策的重要依据。因而对PPI进行有效的预测具有现实的重要意义。由于历年各月份的PPI数值所组成的序列具有非光滑性，文章采用文献[3-4]的思想，选取2014年11至2014年4月的PPI数值，并利用微分进化算法对参数寻优建立起基于非线性灰色微分方程的PPI预测模型，最后以此模型对2015年5、6月的PPI进行预测，结果表明该模型的有效性。

1 非线性灰色微分方程

2 基于非线性灰色微分方程的PPI预测模型的建立

全国2014年11月—2015年6月PPI见表1，数据来源于财经网站http：//data.eastmoney.com/cjsj/ppi.html。

以2014年11月—2015年4月PPI作为训练数据集，以2015年5月—2015年6月PPI作为测试数据。用训练数据集建立非线性灰色微分方程预测模型并对2015年5月和2015年6月的PPI进行预测。具体算法如下。

Step1：输入样本数据（）。设置DE的最大迭代循环次数、种群规模、放缩因子及交叉常数等参数并设置参数的搜索范围。令迭代的代数。

Step2：计算的一阶累加生成序列=（，

），的紧邻均值生成序列（）

及。在所设置的参数的范围内随机生成初始种群，计算和，。以作为训练集，利用（1）分别对和进行拟合得其拟合值和，。计算每个個体的适应度值，记录各个体极值、全局极值和全局极值点。

Step3：通过变异、交叉和选择这三种操作对种群进行更新，计算新种群各个体的适应度值，并更新各个体极值、全局极值和全局极值点。

Step4：若，则，转 Step3。否则，输出全局极值点，即为参数的最优取值。

Step5：利用建立PPI的非线性灰色微分方程预测模型。

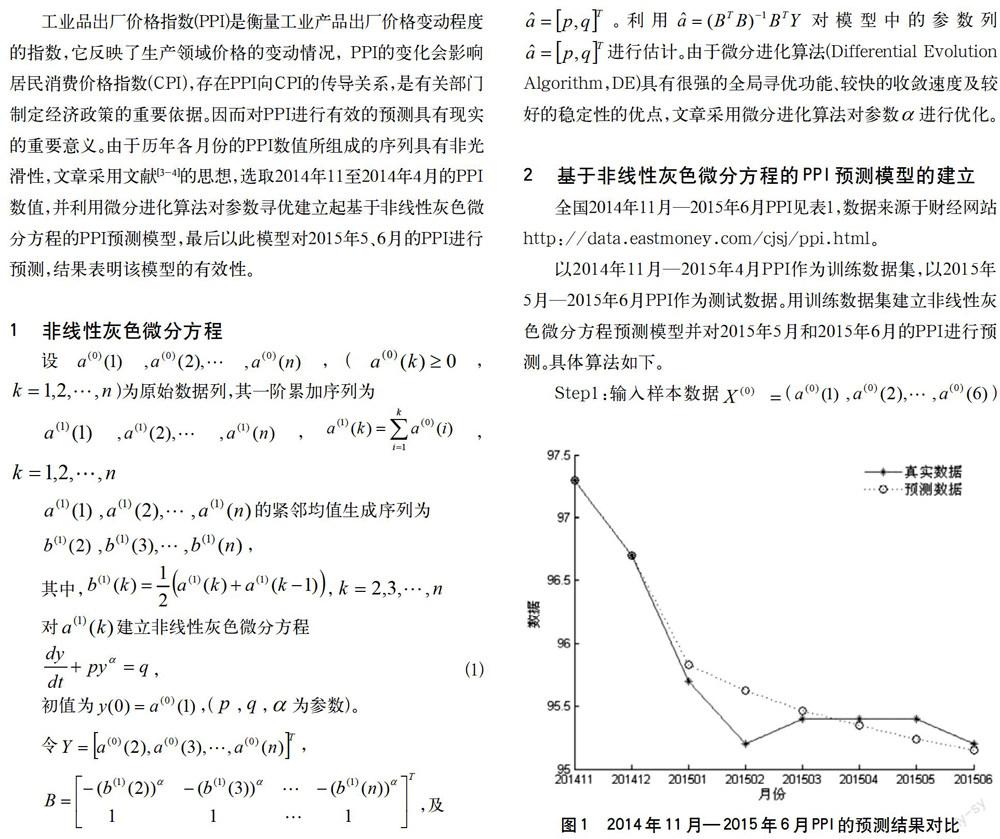
利用matlab 很方便地实现上述算法。2014年11月—2015年4月PPI的预测结果及2015年1月—2015年6月PPI的预测结果见图1和表2。

2015年1月—2015年6月PPI的拟合值与原始值的相对误差如表2。

3 结语

由图1、表2可知，采用本文所建立的非线性灰色微分方程预测模型对2014年11月—2015年4月的PPI进行拟合所得的各拟合值和对2015年5月、6月的PPI进行预测所得的各预测值，与其对应的原始值相比较，相对误差都较小；其中，对2015年5月、6月的PPI进行预测所得的预测值分别为95.2407和95.1526，而2015年5月、6月的PPI的实际值分别是95.4和95.2，相对误差分别为0.17%和0.05%，与实际值较为接近，这也表明了该预测模型的有效性。

参考文献

[1] 杨灿， 陈龙.中国CPI与PPI：因果关系和传导机制[J].厦门大学学报：哲学社会科学版，2013（3）：1-9.

[2] 刘康.PPI、CPI传导机制研究[J].国际金融研究，2014（5）：24-30.

[3] 王美岚.一类非线性灰色微分方程的拟合方式[J].山东师范大学学报：自然科学版，2003，18（2）：17-19.

[4] 杨秋明.非线性灰色微分方程的拟合[J].应用数学，1990（3）：60-67.