基于生态交通效率的城市道路网络优化模型

卢昱寰

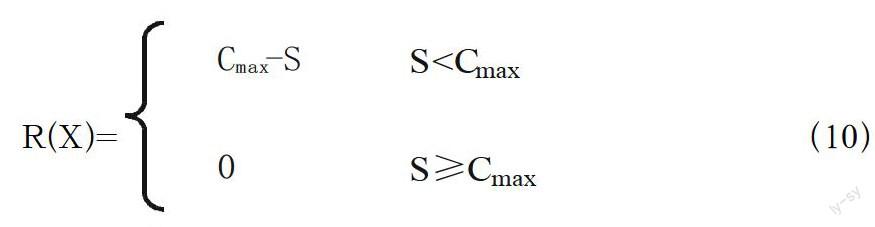
摘 要：在建设和谐社会的今天，保护环境与节省能源，建设生态交通是时代发展的必然趋势。在城市交通道路网络建设过程中，应综合多方面的因素不断加以优化，构建符合时代发展需求的生态交通网络。该文就此加以分析，通过对双层模型的分析得出优化城市交通网络的具体内容，以期对促进城市生态交通网络建设有所促进作用。

关键词：交通工程 城市道路网络优化 生态交通效率

中图分类号：F570 文献标识码：A 文章编号：1672-3791（2015）09（a）-0047-02

1 生态交通效率的内涵

生态交通是社会进步与发展的体现，是可持续发展原则的具体体现，其目的在于缓解城市日益紧张的交通，降低交通对环境的污染，提升城市环境质量与保障社会交通的和谐发展，建立和谐与高效的现代化运输系统也即是在节能环保的理念之上建立城市交通运转体系。“效率”从经济学角度而言，指的是投入与产出比，在资源等量的情况下，比值越高说明产出量越高也即效益越好。由此可知，生态交通效率也即在城市交通运行中，投入一定量的成本以满足社会交通运行的程度以及环境损害与资源损耗的综合水平。

交通效率是考验城市交通运转的重要指标之一，以往的关注点主要集中在交通运输系统以及对人们出行的满足度而忽视了其他因素。就实际而言，影响到交通效率的因素众多，不仅要关注投入生产过程中的各项因素还应关注社会运行中的其他因素，包括环境污染、能源消耗等。由此可见，广义上的生态交通效率可以通过“交通运输效益与社会成本”的比值来进行评价，需要注意的是社会成本应包含建设与运行过程中投入的成本而且包括了环境治理等方面的成本。通过该表达式能够在考核综合成本的基础之上，全方面体现出了交通网络的效率以及优化的方向。

2 道路网络双层优化模型

2.1 上层模型

综合上述定义在对上层模型目标函数的确定上应综合时间成本、能源消耗、建设费用、环境污染物等各项指标，如下所示。

（1）建设投入成本。

其中C代表的建设环节投入的成本、li 代表的是i 路段的长度、f（i）代表的是i 路段的建设函数。

（2）时间成本。

其中T代表的是建设环节中的时间成本、Pk代表的是载客数、Xik代表的是在i路段运行的交通量、Tik代表的是在i路段上通行的平均时间。

（3）能源消耗成本。

式中：E为能源消耗成本；k（vik）为第k 类车在第i个路段的车速vik下的能源消耗成本，考虑到数据的可得性，一般情况下δk（vik）可采用同类车平均数据，如根据相关研究成果，中国城市运营车辆平均能源消耗为6.4 L·（100 km）-1 。

（4）污染物排放量。

其中Wj指的是j排放的污染物的量、j 的种类有CO、CO2、NOx和HC，综合以上各个指标对上层模型目标函数优化如下。

其中S代表的是道路网总体投入成本、Si 代表的是i 路段的投入成本。

其中Cmax代表的是道路建设所需投资费用的最大值、Emax代表的是城市运行中对能源消耗的最大承受值、Wjmax 代表的是城市对于污染物排放的最大限度值。

在该优化模型中融合了道路建设成本、运行中能量消耗量、社会环境承载量，综合三者因素加以优化，以在投入成本有限以及保障交通运行需求的基础之上，降低环境污染以及能源消耗最小的方案，以实现最大的产出比。同时，该模型更综合体现了环保与节能以及高效运输的指标。

2.2 下层模型

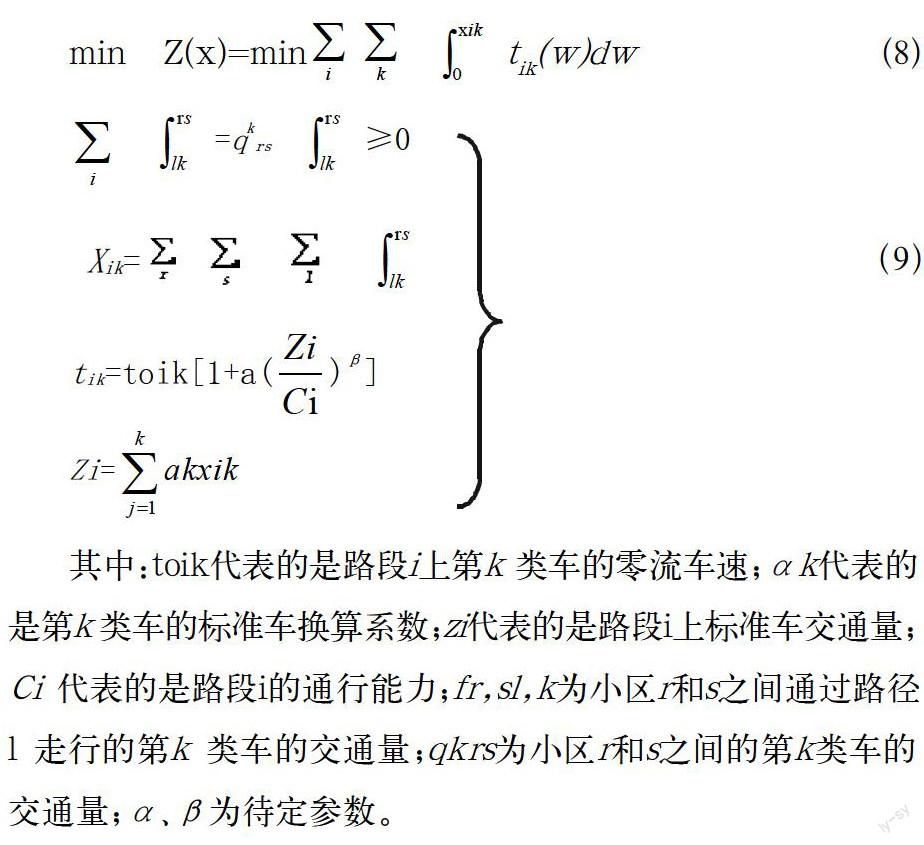
在该文研究中，上层模型是对整體交通网络的优化模型，而下沉模型则是个体出现在线路选择上的平衡模型，具体下层模型构建如下：

其中：toik代表的是路段i上第k 类车的零流车速；αk代表的是第k 类车的标准车换算系数；zi代表的是路段i上标准车交通量；Ci 代表的是路段i的通行能力；fr，sl，k为小区r和s之间通过路径l 走行的第k 类车的交通量；qkrs为小区r和s之间的第k类车的交通量；α、β为待定参数。

3 求解算法与实例解析

3.1 求解算法

由于上层模型中的优化目标函数以及相应的约束条件的变量较多而且转化成二次函数的难度较大，因此在解析过程中不适宜采用传统的方式。即使采用遗传算法也因受到了特征变量的影响致使其最终计算出来的结果得不到保障，不一定是最佳值。因此，为了得出最优值，该文在解析过程中采用的是模拟退火算法（SA）和遗传算法（GA）的混合算法。

使用遗传算法和模拟退火算法（GASA）加以解析，具有以下特点：GASA不仅是并行搜索结构而且有两层，GA位于空间上层与SA并行，由此决定了在优化过程中是群体且并行的。同时GASA优化过程中包含了GA 的复制、交叉、变异和SA 的状态产生函数等不同的搜索结构，其优势在于积累优良的冗余信息而且利于形成优良的后代集成父代模式，进一步提升了在该算法的解析效率，由此得出了优良的GASA的策略。GASA 混合策略在该文模型求解过程中的应用方法在下节的应用实例中具体体现。

3.2 实例概况

M市属于中南地区的地级市，当前市区范围内已建有360 km的道路，但是随着经济的快速发展加剧了交通运行的压力。因此，为顺应时代的发展必须要对现有交通网络加以优化，以下内容采用的是2015年的主要4条干道加以研究和优化。

道路1：为南北走向的主干道，发展方向为是否建设快速通道；

道路2：为东西走向的主干道，发展方向为是否建设快速通道；

道路3：位于M市的中心区；

道路4：是M市对外连接的道路，发展方向为是否扩建。

根据以上情况，对4条道路进行编码，分别如下：道路1和道路2使用1位编码，0指的是保持不变、1指的是修建为快速通道；道路3和道路4使用2位编码，00是保持不变、01指的是建设成2车道、10指的是建设为4车道、11指的是建设为双向的6车道。

综合上述需求，在模型的优化过程中应确保目标函数的最优值也即将不影响其他使用的情况下最大程度上的控制费用。对于GA的适度函数（部分策略）的要求为正数而且其值越大则越好也即个体性能越佳，由此这需要将目标函数转化为极大化，同时在一定情况下要将适度非负。具体如下所示。

R（X）= （10）

综合当地的事情，将Cmax初步设定为1200万元。在模型参数确定上，设定群体中个体的数目为10，杂交概率为0.8，变异概率为0.02，指数退温速率0.9，初温为初态目标值的平方值（以万元为单位时的值）。由于本算例中优化的完全方案只有2×2×4×4=64个，因此GA 的最大迭代次数设为10。在费用参数的选择上，根据M市社会经济发展预测，2015年M市人均可支配收入48500 元，于是时间费用δ=12 .1元·h-1。根据交通规划实施方案，M市修建道路的每km平均费用大致为1200万元·车道-1 。

在约束条件的制定上，因M市是地级市且经济水平属于中等，车辆的通行车速平均为30 km·h-1且较为均衡，可无须将车辆油消耗纳入计算因素之中。通过使用TRA NSCAD对通行的车辆进行分类，再使用VBA并结合Excel对分配的数据进行综合计算，得出最终的GASA。

参考文献

[1] 劳可军.宁波探索建设生态交通[J].综合运输，2015（2）：11-16.

[2] 李飞，张峰.居住区“多元化生态交通”的低碳化规划方法[J].规划师，2015（8）：81-86.

[3] 陆化普，蔚欣欣，胡启洲，等.基于模糊界定的城市生态交通综合测度模型[J].交通运输系统工程与信息，2010（3）：86-92.