做习题 悟规律
徐秀芬


同学们,大家在学习“平面直角坐标系”这一章内容时,要认真地把教科书上的习题做一做。做完以后,大家就会发现平面直角坐标系中点的坐标有什么特征了.
一、各象限内的点的坐标特征
例1(习题7.1第2题)根据点所在的位置,用“+”“-”填写表1.
解析:略
通过填写表1,我们可以归纳出各象限内的点的坐标特征:
1.第一象限内的点的坐标的符号为(+,+),第二象限内的点的坐标的符号为(-,+),第三象限内的点的坐标的符号为(-,-),第四象限内的点的坐标的符号为(+,-).
2.第一象限和第三象限内的点,其横坐标与纵坐标符号相同.
3.第二象限和第四象限内的点,其横坐标与纵坐标符号相反.
例2 已知点M(m,n)在第二象限,则点N(n+1,m-1)在().
A.第一象限
B.第二象限
C.第三象限
D.第四象限
解析:因为点M(m,n)在第二象限,所以m<0,n>0.所以m-1<0,n+1>0.
所以点N(n+1,m-1)在第四象限.
故选D.
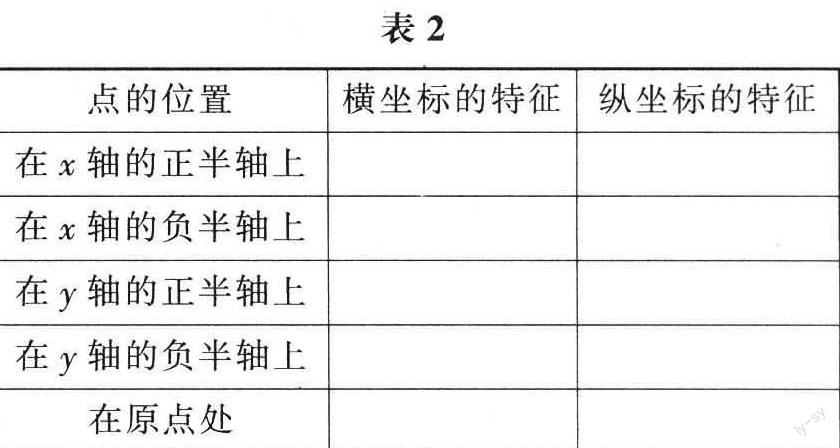
例3 根据点所在的位置,用“+”“-”“0”填写表2.
解析:略.
通过填写表2,我们可以归纳出坐标轴上的点的坐标特征:
1.X轴上的点的纵坐标都为0,所以X轴上的点的坐标可表示为(X,0).若点在X轴的正半轴上,则X>0;若点在X轴的负半轴上,则X<0;若点在原点处,则X=0.
2.y轴上的点的横坐标都为0,所以y轴上的点的坐标可表示为(0,y).若点在y轴的正半轴上,则y>0;若点在y轴的负半轴上,则y<0;若点在原点处,则y=0.
3.原点的横坐标、纵坐标均为0.
例4 已知点A (1+m,2m-1)在X轴上,那么m=_____,点A的坐标为_____.
解析:因为点A在x轴上,所以2m-1=0.解得m=1/2.故1+m=3/2.
所以点A的坐标为(3/2,0).
三象限的角平分线上的点的坐标特征
虽然我们在前面讨论了各象限内的点的坐标特征,但是因为各象限内有一些比较特殊的点,所以我们把这些点列出来进行讨论.
例5 (习题7.1第5题,有改动)如图1,根据要求描点,并总结规律.
(1)在所给的平面直角坐标系中描出点A(-4,-4),B(-2,-2),C(3,3),D(5,5),E(-3,-3),0(0,0).这些点各自的横坐标、纵坐标有什么关系?这些点有什么关系?
(2)在所给的平面直角坐标系中描出点G(-4,4),H(3,-3),M(-5,5),N(2,-2).这些点各自的横坐标、纵坐标有什么关系?这些点有什么关系?
解析:(1)如图2,这些点各自的横坐标、纵坐标相等,如果将这些点连起来,可以发现它们都在第一、三象限的角平分线上.
(2)如图3,这些点各自的横坐标、纵坐标互为相反数,如果将这些点连起来,可以发现它们都在第二、四象限的角平分线上.
通过解答例5,我们可以归纳出各象限的角平分线上的点的坐标特征:
1.第一、三象限的角平分线上的点,其横坐标、纵坐标相等.
2.第二、四象限的角平分线上的点,其横坐标、纵坐标互为相反数.
例6 已知点P( 3n+2,7 -2n)位于象限的角平分线上,则点P的坐标为_____.
解析:当点P在第一、三象限的角平分线上时,可得3n+2=7-2n.解得n=1.
此时点P的坐标为(5,5).
当点P在第二、四象限的角平分线上时,可得(3n+2)+(7-2n)=0.解得n=-9.
此时点P的坐标为(-25,25).
综上可知,点P的坐标为(5,5)或(-25,25)
四、平行(垂直)于坐标轴的直线上的点的坐标特征
例7 (习题7.1第8题)建立一个平面直角坐标系,描出点A(-2,4),B(3,4),画直线AB.若点C为直线AB上的任意一点,则点C的纵坐标是什么?想一想:
(1)如果一些点在平行于X轴的直线上,那么这些点的纵坐标有什么特征?
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标有什么特征?
解析:略.
通过解答例7,我们可以归纳出平行(垂直)于坐标轴的直线上的点的坐标特征:
1.平行于X轴(垂直于y轴)的直线上的点,其纵坐标都相等.
2.平行于y轴(垂直于X轴)的直线上的点,其横坐标都相等.
例8 已知点A(m,-2),B(3,m-1),且直线AB平行于X轴,则m的值为_____.
解析:因为直线AB平行于X轴,所以A、B两点的纵坐标相等,即m-1=-2.解得m=-1.糊麟鬻l
例9 (习题7.2第11题)如图4,三角形COB是由三角形AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,三角形AOB中任意一点M的坐标为(X,y),点M经过这种变换后得到点N,点N的坐标是什么?
解析:经过观察可以发现,三角形COB是由三角形AOB经过对称变换后得到的图形,对称轴就是X轴.
在此基础上观察点A与点C的坐标之间的关系,可以发现它们的横坐标相等,纵坐标互为相反数.
进一步探索可以发现,若三角形AOB中任意一点M的坐标为(X,y),则点M经过这种变换后得到的点Ⅳ的坐标为(X,-y).
通过解答例9,我们可以归纳出关于坐标轴或原点对称的点的坐标特征:
1.如果两个图形关于X轴对称,那么其对应点的横坐标相等,纵坐标互为相反数.
2.如果两个图形关于y轴对称,那么其对应点的纵坐标相等,横坐标互为相反数.
3.如果两个图形关于原点对称,那么其对应点的横坐标、纵坐标均互为相反数.
例10 已知点A(n,-7,m,+1),B(-3,2m-5)关于y轴对称,求m-n的值.
解析:因为点A(n-7,m+1),B(-3,2m,-5)关于y轴对称,所以其纵坐标相等,横坐标互为相反数.从而可得n-7+(-3)=0,m+1=2m-5.
解得n=10,m=6.所以m-n=-4.

