帮你学习点的坐标

吴健

平面直角坐标系是沟通代数学和几何学的桥梁，是极其重要的数学工具.

平面直角坐标系中有关点的坐标的问题在各类考试中经常出现，下面分别举例说明如下.

1.特殊点的坐标.

（1）原点的坐标.原点的坐标是（0，0）.

（2）坐标轴上点的坐标，x轴上点的坐标的特点是纵坐标为0，y轴上点的坐标的特点是横坐标为0.

（3）象限的角平分线上的点的坐标，

第一、三象限的角平分线上点的横坐标和纵坐标相等.如果点的横、纵坐标相等，则它必在第一、三象限的角平分线上，

第二、四象限的角平分线上点的横坐标和纵坐标互为相反数，如果点的横、纵坐标互为相反数，则它必在第二、四象限的角平分线上.

（4）对称点的坐标，

关于x轴对称的两个点的坐标的特点是横坐标相等，纵坐标互为相反数，

关于y轴对称的两个点的坐标的特点是横坐标互为相反数，纵坐标相等，

如果一个点的坐标为（a，6），那么这个点关于x轴、y轴、原点对称的点的坐标分别是（a，-b），（-a，b），（-a，一b）.

例1 若点P（5，a-3）与点Q（b-2013，-2013）关于x轴对称，则a=____，b=____.若点P、点Q关于原点对称，则a=____，b=____.

解：两点关于x轴对称，横坐标相等，纵坐标互为相反数，则5=b-2013，a-3+（-2013）=0，所以a=2016，b=2018.两点关于原点对称，横、纵坐标都变为原来的相反数，则5+b-2013=0，a-3-2013=0，所以a=2016，b=2008.

2.与几何图形有关的点的坐标.

在平面直角坐标系中，以任意两点P（x1，Y1），Q（X2，y2）为端点的线段中点坐标为（x1+x2/2，y1+y2/2）.

例2 如图1，矩形ONEF的对角线交于点M0，ON、OF分别在x轴和y轴上，O为坐标原点，点E的坐标为（4，3），则点M的坐标为____.

解：因为四边形ONEF是矩形，所以点M是OE的中点.

因为点O、E的坐标分别为（0，0），（4，3），所以点M的坐标为（2，3/2）.

3.与面积有关的点的坐标.

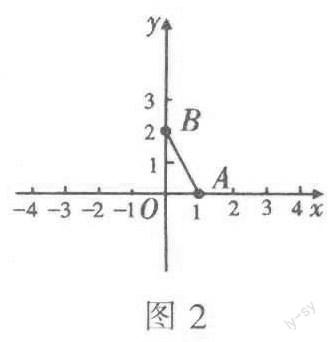
例3 如图2，已知点A（1，0），B（0，2），若点P在x轴上，且三角形PAB的面积为5，则点P的坐标为____，

解：三角形PAB的一边在x轴上，点p距点A有5个单位长度，点P可能在点A的右侧，也可能在点A的左侧，所以有两个解，

填“（-4，0）或（6，0）”.