750kV联合变电构架风振系数计算研究

杨彪　陈寅　闫勇

摘 要：文章以新疆地区某750kV联合变电构架为原型，对其进行静力分析以及基于随机振动理论和Davenport谱的有限元功率谱密度分析，得出750kV联合变电构架的风振系数，所得结论具有重要工程价值，可直接应用于750kV联合变电构架的工程设计以及为更高电压等级的1000kV钢管格构式构架设计提供指导和借鉴。

关键词：750kV变电构架；随机振动；Davenport谱；风振系数

750kV目前属国内仅次于1000kV的电压等级，广泛应用于我国西北地区电网。750kV变电构架是750kV变电站土建设计的最关键点之一，目前750kV变电构架的挂线点高度为40m左右，塔身总高在56m左右，其自振频率一般低于0.40Hz，即自振周期小于2.5s，而风的振动谱密度的扩展范围为周期若干秒到0.08s之间，卓越周期为0.5s左右，由此可见750kV变电构架风荷载的影响非常显著。文章以新疆地区某750kV变电站中的750kV构架为原型，根据随机振动理论计算该变电构架的位移风振系数，得出该变电构架的风振系数。为后续类似的750kV以及更高电压等级的1000kV钢管格构式构架设计提供指导和借鉴。

1 平均风荷载的位移计算

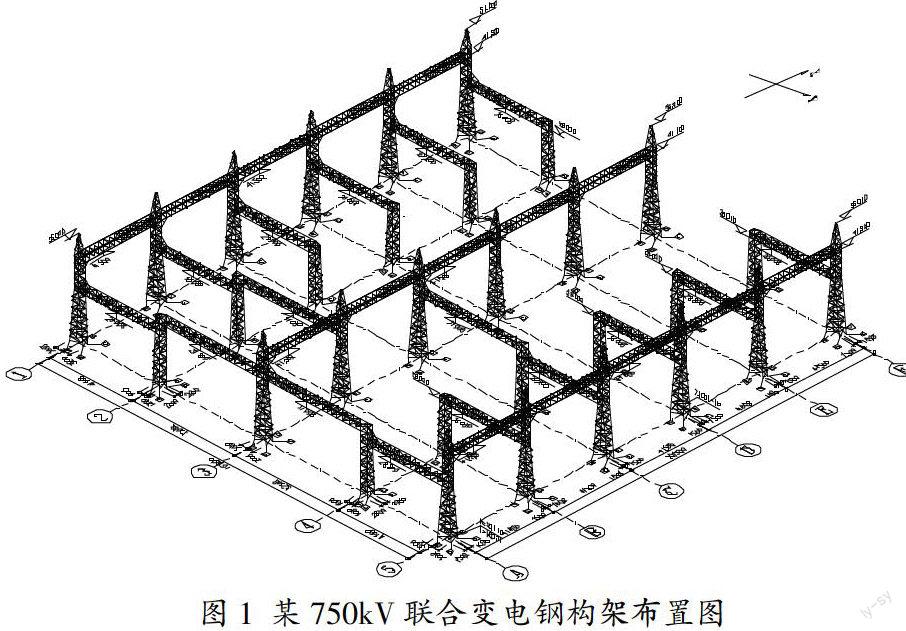
平均风荷载对750kV联合变电构架的作用相当于静力作用，该750kV变电站所处地区设计基本风压为0.5kN/m2，地貌为A类，该750kV联合变电构架布置见图1。

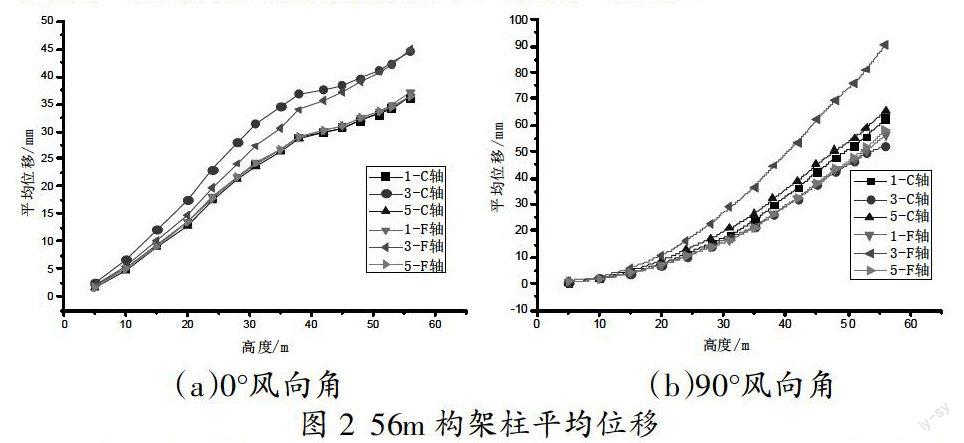
通过对比分析图2～3可知：构架柱各层节点同一方向的位移平均值分布为底部小顶部大；90°风向角下56m构架柱平均位移要大于0°风向角下；两个风向角56m构架柱平均位移最大值均出现在3-F轴构架柱，其值为90.2mm。

2 位移风振响应分析

2.1 脉动风荷载谱的确定

《建筑结构荷载规范》中采用加拿大学者Davenport提出的顺风向脉动风速功率谱密度函数来推导脉动风荷载功率谱密度函数，结合随机振动理论可得位移风振系数计算公式如下：

2.2 750kV联合变电构架位移风振系数

根据式（3）～（4）对750kV联合变电构架进行有限元频谱分析计算，可得该750kV联合变电构架的风振系数，图3～8分别为56m高出线柱以及典型横梁的位移风振系数：

由图3～6可看出：除轴线3外，从靠近边柱（轴线F处）到中间柱（轴线C处），所有构架柱在在0°风向角和90°风向角下时，风振系数都是沿高逐渐增大的，但每个构架柱上各点的风振系数的数值变化不大，0°风向角下风振系数大小为1.50，90°风向角下风振系数大小为1.55；3-F轴构架柱风振系数要大于中间柱的值（约增大20%），0°风向角下风振系数大小为1.50，90°风向角下风振系数大小为1.75；通过对2种风向角下风振系数的对比分析，构架柱在90°风向角下风振系数略大于0°风向角的数值，对于横梁处风振系数一般取风向与其垂直时的风振系数，其值可取为1.50（除3-E～F横梁外）。为了便于设计，除3-F轴构架柱以及3-E～F横梁外，750kV联合变电构架风振系数可取为：1.55，3-F轴构架柱以及3-E～F横梁风振系数取为：1.75。

3 结束语

文章通过大型有限元软件SAP2000，以随机振动理论为依据，在频域内对A类地貌下750kV联合变电构架的节点风致振动响应进行分析计算，可以得出以下结论：

（1）750kV联合变电构架0°以及90°风向角时，构架横梁越靠进中间的节点，其位移平均值也越大；构架柱各层节点同一方向的位移平均值分布为底部小顶部大，位移由下到上逐渐变大。

（2）构架柱在90°风向角下风振系数略大于0°风向角的数值，而建议对于横梁处风振系数一般取风向与其垂直时的风振系数。

（3）对于750kV变电构架的构架柱，一般来说，越靠近中间，风振系数越大；从靠近边塔侧到中间塔处，风振系数逐渐变大，实际设计时为了计算方便可统一取中间构架柱或横梁的大值作为设计时的风振系数。

（4）A类地貌下750kV联合变电构架整体风振系数可取1.55。

（5）对于类似轴线3-F处的边塔，若无母线塔以及母线梁相连，在实际工程设计计算时应考虑局部增大风振系数的取值（约增大20%），其值可取为1.75，与该构架柱相连的横梁也应考虑局部增大风振系数的取值。

参考文献

[1]GB500092-2012.建筑结构荷载规范[S].北京：中国建筑工业出版社.

[2]DL/T 5154-2012.架空送电线路杆塔结构设计技术规定[S].

[3]张相庭.结构风工程：理论·规范·实践[M].北京：中国建筑工业出版社，2006.

[4]陈寅，陈传新，郑威，等，1000kV变电构架风振系数的计算[J].电力建设，2011，9.

[5]变电架构设计手册[M].武汉：中南电力设计院，2006.

[6]朱海维，马勇杰，吴伟康.1000kV构架风振系数的计算研究[J].电力建设，2013，2.