PM2.5污染物的影响因素识别

杨帅帅 倪小雨 李放歌 王玺

摘要：有研究认为，AQI监测指标中的二氧化硫（SO2），二氧化氮（NO2），一氧化碳（CO）是在一定环境条件下形成PM2.5前的主要气态物体。西安市环境监测站对这几种污染物进行了长期监测，并每天公布检测数据。本文以西安市PM2.5监测记录为依据，运用多元回归方法研究PM2.5污染浓度指标的影响因素，并建立回归方程。研究表明，西安市的PM2.5污染物浓度与二氧化氮和PM10的浓度有关。

关键词：空气污染  多元回归  模型修正

近年来，PM2.5污染物受到人们的普遍关注。PM，英文全称为fine particulate matter，即细颗粒物，PM2.5是指大气中直径小于或等于2.5μm的颗粒物，又称为可入肺颗粒物。粒径在10μm以上的颗粒物，会被挡在人的鼻子外面;粒径在2.5μm至10μm之间的颗粒物，能够进入人体上呼吸道，但部分可通过痰液排出体外;而粒径在2.5μm以下的亚微颗粒物，会被吸入人体肺部，进入支气管，干扰肺部的气体交换。虽然PM2.5只是地球大气成分中含量很少的组分，但它对空气质量和人类健康等有重要的影响。

对于空气污染物的监测，我们往往着重研究空气中SO2、NO2、PM10、CO、O31小时、O38小时以及PM2.5的浓度。PM2.5的浓度可能受到其它污染物浓度的影响，如果确定哪些污染物浓度影响PM2.5浓度，就可以为治理PM2.5污染提供有效的突破口。

本文利用空气污染物的监测数据，从统计角度研究 PM2.5浓度的影响因素。

1 数据采集

本文数据采自西安市环境监测站网站（http：//www.xianemc.gov.cn/）公布的空氣质量日报。西安市共有高压开关厂等12个监测点，每个监测点每天对西安市空气污染物进行检测。本文取2012、2013年共24个月的平均值。

空气中SO2浓度、NO2浓度、PM10浓度、CO浓度、O31小时、O38小时与PM2.5有着密切的关系，也从一定的角度反映了一个城市的空气质量状况。

表1.1  各监测点6项检测数值24月平均（部分数据）

■

2 建立回归模型

以PM2.5值（y）作为因变量，SO2浓度（x1：毫克/立方米）、NO2浓度（x2：毫克/立方米）、PM10浓度（x3：毫克/立方米）、CO浓度（x4：毫克/立方米）、O31小时（x5：毫克/立方米）、O38小时（x6：毫克/立方米）作为自变量，采用强制回归的方法，进行多元回归分析，分析结果如下：

表2.1  Model Summary

■

表2.2  ANOVAb

■

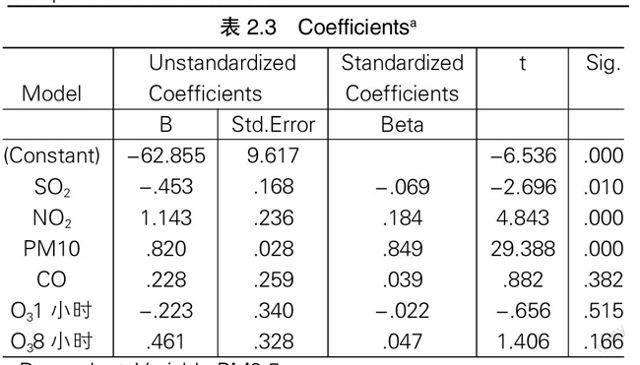
表2.3  Coefficientsa

■

回归方程为

■=-62.855-0.453x■+1.143x■+0.820x■+0.228x■-

0.223x■■+0.461x■

由表2.1可以看出，样本决定系数R=0.994>0.8，即相关程度很好。由表2.2看出F=744.623，Sig.=0.000，可以认为6个自变量对于因变量影响效果显著。由表2.3看出t检验中，变量x1，x2，x3的Sig.值较小，分别为0.000<0.05，0.010<0.05，0.000<0.005，所以x1，x2，x3自变量对于因变量相关程度较高。

但是，通过方程可以看到SO2与O31小时的系数为负数，即当他们增多时PM2.5值减小，故该两项数据与 PM2.5值无关，舍去这两项数据重新做一次回归。

以PM2.5值（y）作为因变量，NO2浓度（x1：毫克/立方米）、PM10浓度（x2：毫克/立方米）、CO浓度（x3：毫克/立方米）、O38小时（x4：毫克/立方米）作为自变量采用强制回归的方法，再次进行多元回归分析（计算表省略），得到如下回归方程：

■=-61.287+0.922x1+0.838x2

样本决定系数R=0.994>0.8，即相关程度很好。F=1007.267，Sig.=0.000，可以认为4个自变量对于因变量影响效果显著。经t检验，变量x1，x2的Sig.值较小，分别为0.000<0.05，0.010<0.05，所以x1，x2自变量对于因变量相关程度较高。因此，删去变量x3（即CO浓度），再次以x1，x2为自变量进行回归分析，得到回归方程如下：

■=-56.714+0.981x1+0.836x2

经逐步线性回归看出2个自变量PM10、NO2与因变量PM2.5之间相关性高。

3 多重共线性诊断与模型修正

当自变量存在多重共线性时，利用最小二乘估计得到的回归参数估计值很不稳定，回归系数的方差随着多重共线性强度的增加而加速增长，会造成回归方程高度显著的情况下，有些回归系数通不过显著性检验，甚至出现回归系数的正负号得不到合理的经济解释。需要对上文得到的两个自变量NO2浓度和PM10浓度进行多重共线性诊断。可以利用方差扩大因子法以及对原始数据（逐步回归后的数据）进行诊断。

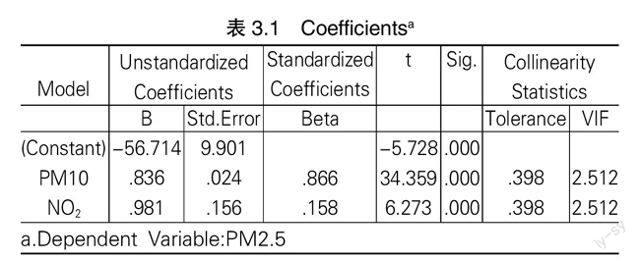
以PM2.5值（y）作为因变量，NO2浓度（x1：毫克/立方米）、PM10浓度（x2：毫克/立方米）为自变量进行共线性诊断，分析结果如下：

综合表3.1可以看出，PM10、NO2的方差扩大因子（VIF）比较小，且均小于10，说明建立的回归模型原始数据中PM10、NO2不存在着明显的多重共线性。因此，有效的回归方程仍然为

=-56.714+0.981x1+0.836x2

4 结论

根据多种污染物浓度的数据进行回归分析，结果表明PM2.5浓度值与PM10和NO2浓度值密切相关，并得到有效的回归方程。这个方法可以对影响PM2.5进行初步筛选。但是不同的地区应该有不同的结果，所以这个回归方程不具有普遍意义。

参考文献：

[1]GB3095-2012环境空气质量标准[S].中华人民共和国环境保护部.

[2]汤伟.雾霾治理研究与国外城市对策[J].城市管理与科技，2014.1：76-79.

[3]林清泉.计量经济学[M].北京：中国人民大学出版社，2012.

[4]郭晓泽，单思行.针对PM2.5的综述[J].能源与节能，2012，86（11）：58-60.

通讯作者：王玺