企业并购活动中幂律现象的实证研究

罗智

摘要：通过对1996年1月1日到2014年12月31日期间中国企业并购活动的详细数据进行统计分析。从个体层面上发现，房地产行业的并购市场十分活动，这与房地产行业的特点有关。在群体层面上发现，中国企业并购活动的时间间隔分布满足幂指数为r=0.5861的幂律分布。

关键词：企业并购活动；时间间隔；幂律分布

1.引言

在自然界和人类的活动中，幂律现象无处不在，从有关财富分配问题的Pareto律（二八法則）和关于英文单词使用频率问题的Zipf律，到后来的Barabási and Albert的BA无标度网络模型[1]，逐步掀起了对幂律现象的研究热潮。在天文学方面，太阳耀斑强度的分布是符合幂律分布的[2]。在社会学方面，战争规模与发生频率的分布和姓氏地域的分布都是幂律现象著名的例子[3-4]。在计算机科学方面，网站中页面的数量、文件大小均服从幂律分布[5]。在网络研究方面，大量的现象是属于幂律现象，例如：万维网[6]、科学家合作网络[7]、食物链网络[8]、蛋白质关联网络[9]、电子邮件网络[10]等等。由此可见，幂律现象是一种无处不在的常见现象。

人们在经济活动方面对幂律现象的研究还很少见，在企业并购方面尤为甚之。那么，在企业并购方面是否存在着幂律现象呢？

2.实证研究

2.1 数据来源

本章所使用的企业并购活动数据来自国泰安数据服务中心（CSMAR Solution）的中国上市公司并购重组研究数据库，该数据库提供了企业并购活动事件的全面信息。从中国上市公司并购研究数据库中选取了1996年1月1日到2014年12月31日的企业并购活动数据作为研究对象，提取的字段包括“证券代码”、“首次公告日期”、“交易是否成功”和“关联交易标识”。为了描述的方便，此数据集记为数据集1。

2.2 数据筛选

为了提高实证结果的精确度，本章只选取“交易成功”和“非关联交易”的企业并购活动数据作为实证研究的样本数据，也就是说从数据集1中选择“交易是否成功=Y”且“关联交易标识=N”的数据作为本章研究的样本数据，最终获取了2508家企业23374起并购活动的数据。

2.3 数据统计分析

2.3.1 个体层面的数据统计分析

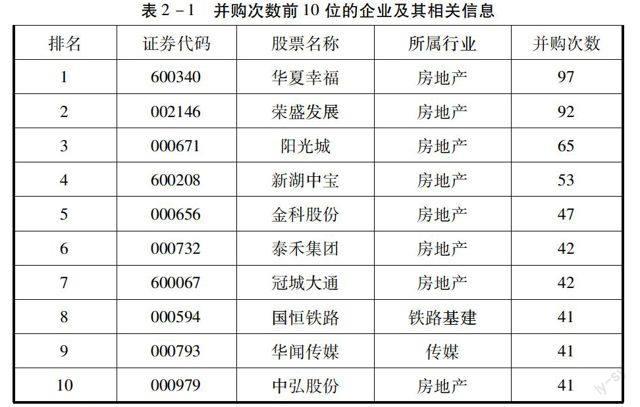
为了研究单家企业并购活动的统计特征，在样本数据中找出在1996年1月1日到2014年12月31日期间参与并购活动总次数排名前10的企业及其相关的并购信息，详细的统计结果如表2-1所示。

从表2-2中可以知道，在并购次数前10位的企业中有8家企业来自于房地产行业，房地产行业中企业并购市场的活跃程度由此可见一斑，这与房地产行业的性质特点有着密切的关系。房地产行业并购市场活跃的原因主要有以下几点：第一，资源整合是房地产企业频繁实施并购活动的原动力，收购企业可以通过并购活动获得目标企业的土地、物业等重要资源，从而扩大企业的规模，提高企业的市场份额；第二，由于房地产行业属于资金密集型的行业，房地产企业容易陷入资金紧张的局面，企业的并购活动能够迅速解决资金短缺所带来的问题；第三，2007年由美国次贷危机引起的国际金融危机爆发后，国家为了维护房地产行业的稳定，出台多项相关政策促进房地产行业的产业整合，大量的房地产企业顺应政策趋势从而频繁地实施企业并购活动。

2.3.2 群体层面的数据统计分析

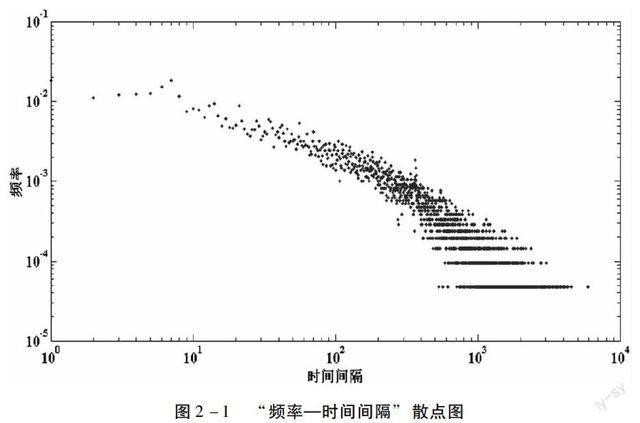
为了找到企业并购活动中的幂律现象，需要所有企业并购活动的时间间隔，利用样本数据中“证券代码”和“首次公告日期”两个字段可以找到所有企业并购活动的时间间隔。以“时间间隔”（单位为天）为横坐标，其相应的“频率”为纵坐标，在双对数坐标系下画出“频率—时间间隔”散点图，如图2-1所示。

从图2-1中可以看到，“频率—时间间隔”图具有明显的胖尾特性，胖尾特性是幂律分布的重要特征之一。利用Matlab软件进行拟合，得到拟合曲线为p（x）=0.02567x-0.5861，其中拟合曲线的误差参数详见表2-3。

从表2-3的误差参数中可以知道，曲线的拟合度（R-square）达到了82.12%，其次，误差平方和（SSE）和标准误差（RMSE）都非常接近于零，因此，“频率—时间间隔”散点图服从幂律分布，即企业并购活动时间间隔服从幂指数r=0.5861的幂律分布。

3.结论

本文通过对中国企业并购活动时间间隔的实证研究发现，其“频率—时间间隔”散点图存在胖尾特性，并通过曲线拟合发现中国企业并购活动时间间隔是一种幂律现象。至于其幂律现象的产生机制尚在探讨当中，这也将是本文后续的研究目标。（作者单位：广东工业大学管理学院）

参考文献：

[1] A L Barabási and R Albert. Emergence of scaling in random networks[J]. Science， 1999， 286（5439）： 509-512.

[2] Lu E.T. and Hamilton R.J. Avalanches and the Distribution of Solar Flares[J]. Astrophys， 1991， 380： 89-92.

[3] Roberts D.C. and Turcotte D.L. Fractality and Selforganized Criticality of Wars[J]. Fractals， 1998， 6： 351-357.

[4] Zanette D.H. and Manrubia S.C. Vertical Transmission of Culture and the Distribution of Family Names[J]. Physical A.， 2001， 259： 1-8.

[5] Crovella M. and Bestavros A. Self-Similarity in Word Wide Web Traffic： Evidence and Possible Causes[J]. IEEE/ACM Transactions on Networking， 1997， 5（6）： 835-846.

[6] Adamic L.A. and Hubennan B.A. Power-Law Distribution of the Word Wide Web[J]. Science， 2000， 287： 2113-2115.