见与不见

王开杰

前景提要：

作为参加工作17年的我，可以毫不夸张地说自己是看着、听着、学习着吴正宪老师的数学课一步步成长的。2014年11月17日经纬小学，我有幸第四次在哈尔滨现场聆听吴正宪老师的数学课。回想前面三次，场景依然历历在目。翻出过往的文字，细细品读，仍然让我心潮澎湃。再次写下一组文字，记录下我的敬意，也书写下我的成长！

见与不见——见

再次见到吴老师，见到了吴老师一直挂在嘴边的熟悉微笑，见到了吴老师的数学课堂，见到了学生真正喜欢的课堂，见到了学生们课堂结束时的恋恋不舍。毫无疑问，再次见到的是带有吴老师明显风格特征的数学课堂。这种风格特征一切如常，亲切自然，真挚生动，智慧深刻，回味绵长。如5年前香滨小学的初见，又仿佛2年前、1年前的再相见，抑或是与吴老师同台杭州“千课万人”展示活动，吴老师的风格特征愈加清晰，愈加让人印象深刻，今天这种风格特征更是弥漫充盈在整个会场中，无处不见！

对于“商不变的规律”这一教学内容而言，有一个最难把握又是不可回避的问题：大多数学生对于规律（被除数和除数都乘或除以一个相同的不为零的数，商不变）早有了解。这份了解源于已有大量相关除法知识的积累，源于逐步形成的运算能力发挥的潜移默化作用，也可能源于过早的提前学习等。面对这份学生的了解，老师们的选择大多是两类，要么是对于学生已有认知视若不见，全当新知来展开教学；另一种则是将这部分规律教学视如鸡肋，一带而过。

而见到吴老师的课堂却是另一番景象：简洁情境引入，再辅以二维的正比例数量关系，继而借两组例子引发学生的思考，充分引导学生暴露自己对于问题的初始想法，再通过同伴之间的比较辨析、交流碰撞进而逐步完善、建立模型。“面对很多学生已经知道的问题，要不要学，该怎样学？”吴老师的这节课做了精彩的回答，对于老师们来说极具借鉴价值。

见与不见——不见

李玉贵老师（台湾）曾说过：“ 一个好的课堂，是上着上着老师就不见了 。”在这节“商不变的规律”课堂上，我看见了这样的吴老师，又或者说“我看不见吴老师了”。

吴老师真正退到了后面，学生们走向了前台。学生由略显青涩的表达开始，到侃侃而谈，针锋相对，再到互帮互助，智慧迸发，思维的火花不时闪现。生生的精彩互动，正是吴老师课堂中最美、最独特的风景！

从本节课学生的认知起点来看，不同学生所处的认知阶段各不相同：有完全不知道规律的，有了解一点的，有熟悉掌握的，更有可以进行数学表达进而实际应用的……如何让不同的学生得到发展，这正是“看不见的吴老师”在发挥着作用。这“看不见”中，有吴老师对教学内容的深刻理解；这“看不见”中，有吴老师对学生学情的充分预设；这“看不见”中，更有吴老师对课上问题的及时判断、敏锐把握与适时介入。面对学生都要求回答的场面，该选谁来讲呢？那发人深省的“意义同学”怎么会出现得这样恰到好处呢？教师退到后面，则须要更敏锐地关注前面。课堂上该如何不着痕迹地巧妙引导，吴老师为我们上了精彩的一课！

见与不见——我见

课后，我争取到了与吴老师对话的机会：

“吴老师您好！向您提一个问题：在场有很多老师，大家往往受课时计划所限，不能有很大的驾驭空间。就如，这一内容的课时安排只是一课时，如何处理本节课未完的其他内容，如果一定要在一节课既讲完又练到，哪些部分可以删减呢？”

吴老师给出了大课程观的提法，讲到课程安排有时可做加法，有时可做减法的答案。更是呼吁要给教师上课、备课多些空间的提法……

会后，有老师与我交流，讲我是在明知故问，说我是借吴老师的话，回应诸多领导对老师们平时的“苛刻”要求！我一笑置之。在此不作评价，以下只是表达我参与此次课堂教学观摩的感受：

1. 教什么——看清方能提升

一节数学课“教什么”本不应该是有争议的话题，因为这是开展一切教学活动的前提。但观摩吴老师的课却可以带给教师们一些启示与思考，即数学教学的设计要从整体（知识体系建构与学生长远发展）来思考，可以不拘泥于一节课，一个知识点，可整合、可取舍、可加减。

商不变的规律即“被除数和除数同时乘或除以一个相同的数（0除外），商不变”。吴老师与学生们呈现的课堂中并没有处理规律中的除法（被除数和除数同时除以一个相同的数），也没有处理“0除外”这一特殊情况。这样的选择（教什么）看上去有些异于常理，课后吴老师从课程观的角度（前面提到的），以及培养学生的角度出发，对其中的原因做了细致的解读。吴老师的见解高屋建瓴、引人深思，应该说带给一线老师们极大的启发。

在这里要补充一点我的理解，其实吴老师对于这一教学内容的取舍及教学目标（教什么）的设定，在一定程度上是受其教学风格（怎么教）影响的。吴老师的课堂总是能够极大地凸显学生中心的理念，开放、包容的课堂总是充满了活力。同时学生又并不是单一的中心，吴老师的教学又总能巧妙地体现一种平衡（时而见时而不见），既以学生为中心又以教师为中心，这两个中心通过有效的问题预设和敏锐的问题捕捉做了很好的衔接。

但这样课堂就会遇到一个难以回避的掣肘，即借班上课的师生须要建立默契（更多指向的是学生对于老师教学理念、教学方法的适应）。师生难免要有一个试探（甚至是反复试探）的过程，而这一打破陌生建立默契的过程恰恰又是吴老师课堂极为闪光之处。可随之而来的也就是要想在规定的时间（40分钟）完成规定的内容（教材中的内容）那显然是不可能的事情。由此，我们解读很多观摩课并不以限定的时间作为严格的卡尺，这是有原因的。

由此也产生了一个期待：名师们带着自己的学生上课，那定会是更胜一筹的美妙。

可对于更普适的数学课堂，教什么呢？一节课40分钟，按照教材编排展开教学，按照课时计划走的教师还是大多数（绝大多数），从这一角度去思考一节常态、适合大多数老师自己的实践课，也许会更受益！更普适地教，开展更普适的教研活动希望成为一个方向。

向吴老师学习，学习、揣摩、实践这师生双中心显然任重而道远，须要脚踏实地，非一日之功。如果回到更为平常的课堂，暂且抛开高大上的理念与做法，先来弄清这一内容（商不变的规律）的教学目标到底是什么。我觉得应达到的知识与能力目标至少有“经历探索‘商不变的规律全过程；在观察、比较、讨论、交流中发现‘商不变的规律；能运用这一规律进行一些除法的简便计算。更进一步可能还有“相关规律的迁移类比（见2.怎么教）等”。

由此，我想表明一种观点，吴老师的课（教什么）显然不是商不变的规律唯一的上法。老师们的特点不一、风格迥异。每一位教师都应该有对待问题的独立思考与冷静判断，否则就只会学到热闹，偏离门道。吴老师基于大课程观的理解，基于自己对课堂、教材的把握，基于借班上课的学生实际，她的课不会适合下面的每一位老师，也不可能适合每一位老师。面对精彩的课堂，我们不应只是心动、激动，简单地模仿，更要看清、学习、借鉴执教者的思考与研究，进而结合自己现有的实际来提升视野，丰富课堂，乃至形成风格。

2. 怎么教——还可以怎样教

“就这节‘商不变的规律，吴老师是怎么教的，还可以怎样教呢？如果我来上，会有怎样的突破呢？”这是观摩学习中，我一直不断思考的另一个问题。冒昧借吴老师课的思路为线索，展开一些自己的思考，欢迎批评指正。

吴老师在这节课的课后交流中提到，特别看重通过学生自主合作交流，通过数学表达（语言表达、文字表达、图示表达）来建构数学模型（商不变的规律），感受数学思想，尤其提到将这节课重点放在理解商不变的规律中“乘”的基本规律上。这一解读切中教学内容的数学本质，体现了吴老师对于知识的深刻把握，课堂的呈现也更是淋漓尽致地体现了吴老师的设计意图。

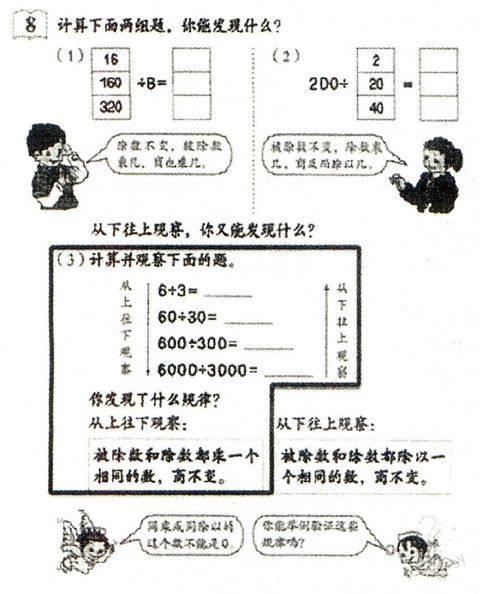
对照一下人教版教材（左图），显然吴老师处理的是“例8（3）”中的左半部分“被除数和除数都乘一个相同的数，商不变”。

借此我们再来分析一下教材，同一页教材中“例8（1）、（2）、（3）”，这三道小题给出了三个层次，两个角度对除法规律的解读。这里是否可以一起引入它们，借助辨析比较会不会对商不变规律的建模更有帮助呢？

随之而来的问题就是，吴老师的这节课已然满满，如何再加入这样的内容呢？换种问法，这节课中可不可以对某些环节进行整合，有些方式是不是可以变化呢？

吴老师课堂中看重学生的数学表达，学生的交流互动，但有了更好（多样、有层次）的数学表达就代表学生对商不变规律有了更本质的提升吗？试想，不同的学生的表达方式并不相同，学习风格也不尽相同。可能有更善表达的学生，也自然会有学生属于“茶壶煮饺子”倒不出来的，这不应是辨别学生学习、理解掌握知识情况的唯一途径。借助外在的数学表达让学生来质疑与深化规律的理解，应该只是一种方式，而非唯一的方式。整合一些表达环节，压缩一些时间，进而借助前面的三道小题，三个层次，两个角度，引导学生揭示规律，体会规律的不同变式，对于深入理解规律也许是一种有益的尝试。丰富的变式对于概念的建构将起到重要的作用。

再如从“商不变”可以联想到“被除数不变、除数不变”；同样也可以联想到“积不变，和不变，差不变”；进而继续延伸到“商变”等一系列规律的探索。这样的联想类比会更丰富学生对于运算本质的理解，提升学生的运算能力。更远些，在学习了小数、分数运算以后，规律也可以再提升。“数学思想主要反映了认识的深度，那么，就只有从较为广泛的角度去进行分析，也即十分重视视角的广度，我们才能达到较大的深度，也即准确地揭示出相关知识内容中所蕴含的数学思想。”（郑毓信语。）

当然知易行难，说永远比做要容易。再次感谢吴老师的课堂带给我的启示与思考，实践的道路永远艰辛，与走在这条路上的老师们一起共勉。