在辩证统一中把握不等关系
孔凡哲 曾金炳


不等式是初中数学的重要内容之一,它是一元一次方程、二元一次方程组等内容的进一步发展.
不等式与方程、函数作为刻画现实世界的数学模型,三者构成初中数学课程教学的最重要内容.
一、不等是大千世界中普遍存在的关系
对于某一变化过程中的两个量a、b而言,随着运动变化,a与b之间的关系有时相等,有时不等,这种数量关系就成了数学的研究对象之一.
1.不等是普遍的关系,而相等却是暂时的、瞬间的关系.
对于运动变化过程中的两个量a、b而言,其彼此相等往往是暂时的,而不等却是普遍存在的.
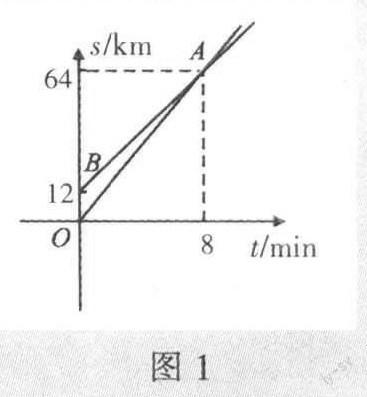
例1 甲、乙两位老师相约乘坐城际高铁到省城参加教研活动.乙住处距省城64km,甲住处位于乙住处与省城之间,两个住处相距12km.两人乘坐高铁(匀速行驶)同时同向出发,其距乙出发点距离与时间关系如图1所示.那么,两人8min后能同时到达省城吗?其各自所乘坐高铁的速度分别为多少?
2.寻找差异是衡量不等关系的重要工具,求差法、求比法是判断不等关系的重要方法.
对于不等关系a>b,通常采取求差法进行分析研究,当a、b均为正数时,也可以采取求比法进行分析研究.
二、准确把握不等式所蕴涵的基本思想
学习不等式,除了理解、掌握不等式的基本概念和基本性质,还要注意体会把握不等式的重要思想方法.
1.模型思想.
与相等关系相比,不等关系是现实世界中更为普遍的关系,不等式是刻画不等关系的重要模型.这种模型经常与方程、函数联系在一起,三者都是刻画现实世界中量与量之间变化规律的重要模型.在解决实际问题时,往往需要合理选择这三种重要的数学模型.
例2某工厂现有甲种原料360kg,乙种原料290 kg,计划利用这两种原料生产A、B两种产品,共50件,已知生产1件A种产品,需用甲种原料9kg,乙种原料3kg;生产1件B种产品,需用甲种原料4kg,乙种原料10kg.如果设生产A种产品x件,则按要求分别需要甲、乙两种原料各多少?
按要求安排生产A、B两种产品,可以有哪几种方案?请你帮助设计.
解析:在这里,最重要的信息就是“计划利用这两种原料生产A、B两种产品,共50件”,这里包含着两个关键的数量关系:生产A、B两种产品所使用的甲种原料的数量不超过360 kg,生产A、B两种产品所使用的乙种原料的数量不超过290 kg.
如果设生产4种产品x件,那么,生产B种产品(50-x)件,于是,按要求需要甲种原料[9x+4(50-x)]kg,乙种原料[3x+10(50-x)]kg.从而,上面的两个关系可以等价地表示为:生产A、B两种产品所使用的甲种原料的千克数9x+4(50-x)不超过360.生产A、B两种产品所使用的乙种原料的千克数3x+10(50-x)不超过290.
由上述过程知,建模包含了这样的过程:
首先,用自然语言描述现实问题;其次,发现现实问题中的量,用自然语言描述多个量之间的不等关系;再次,用只含一个未知数的式子描述这些量之间的不等关系;最后,用不等式(组)表示不等关系.
2.辩证思想.
相等关系与不等关系是一对矛盾关系,但是,在引入松弛量的前提下,“a>b”与“存在一个正数c,满足a=b+c”却是等价的,这就是一种辩证思想.这意味着,即使是相互矛盾的一对关系,在一定条件下也可以相互转化,
值得一提的是,恰当地运用这种思想,可以轻松解决相当多的问题,教材中本章的大部分问题,几乎都可以利用这种思想加以解决.不等式的所有性质几乎都可以采取引入松弛量的方法加以证明.
3.数形结合思想.
数轴是描述不等式(组)的解集的最佳方式之一.其主要的依据在于,每一个实数都能用数轴上的点表示,数轴上的每一个点都对应着一个实数.右边的点对应的数总比左边的点对应的数大.
从而,所有大于a的数对应的点,都排在数轴上数a对应的点A的右侧.
按照这种思想,解不等式(组)就变得自然、简单.
事实上,我们在解不等式(组)时,运用数轴表示不等式(组)的解集,就是数形结合思想的具体体现.
可见,在解决与不等式(组)有关的问题时,我们要注意数形结合,尤其要注意联系数轴或者方程、等式等内容,注意不等式与等式之间的转换.同时,要深刻体会不等关系的广泛存在性,注意使用恰当的不等式来刻画这种不等关系.
还记得解方程的核心方法是“化归”吗?解不等式其实也是如此,事实上,无论是一元一次不等式的解题过程,还是一元一次不等式组的解题过程,都是凭借不等式的相关性质,化繁为简、合并消元,最终化归为x>a等的形式.

