机械能恒定律核心考点点击

徐汉屏

核心考点一：机械能是否守恒的判断

动能与势能（包括重力势能与弹性势能）统称为机械能。判断系统的机械能是否守恒，通常可采用下列三种不同的方法：

①做功条件分析法——应用系统机械能守恒的条件进行分析。若物体系统内只有重力和弹力做功，其他力均不做功，则系统的机械能守恒。

②能量转化分析法——从能量转化的角度进行分析。若只有系统内物体间动能和重力势能及弹性势能的相互转化，系统跟外界没有发生机械能的传递，机械能也没有转变成其他形式的能（如没有内能增加），则系统的机械能守恒。

③增减情况分析法——直接从机械能各种形式能量的增减情况进行分析。若系统的动能与势能均增加或均减少，则系统的机械能不守恒；若系统的动能（或势能）不变，而势能（或动能）却发生了变化，则系统的机械能不守恒；若系统内各个物体的机械能均增加或均减少，则系统的机械能也不守恒。当然，这种方法只能判断系统的机械能明显不守恒的情况，对于另一些情况（如系统的动能增加而势能减少）则无法做出定性的判断。

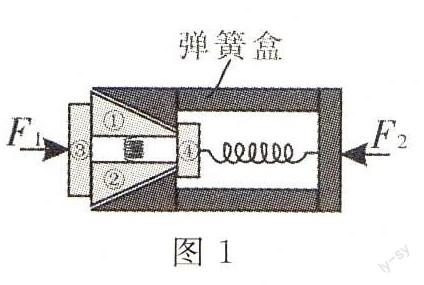
例1 2014年高考广东卷第16题）如图1所示是安装在列车车厢之间的摩擦缓冲器结构图。图中①和②为楔块，③和④为垫板，楔块与弹簧盒、垫板间均有摩擦。在车厢相互撞击使弹簧压缩的过程中（）。

A.缓冲器的机械能守恒

B.摩擦力做功消耗机械能

C.垫板的动能全部转化为内能

D.弹簧的弹性势能全部转化为动能

缓冲器系统除弹力做功之外，还有车厢的撞击力及摩擦力做功，故缓冲器的机械能不守恒，A错。摩擦力做功，使部分机械能转化为内能，因而消耗了机械能，B对。垫板的动能转化为内能和弹簧的弹性势能，没有全部转化为内能，C错。弹簧压缩过程中，是垫板的部分动能转化为弹簧的弹性势能，而非弹簧的弹性势能转化为动能，D错。本题正确选项为B。

本题考查了机械能是否守恒的判断，考查了能量转化的分析。一般说来，当有外力对系统做正功时，系统的机械能增加；当有摩擦力对系统做负功时，系统的机械能减少。

核心考点二：机械能守恒定律的应用

机械能守恒定律：在只有重力和弹力做功的物体系统内，动能与势能可以相互转化，而总的机械能保持不变。

机械能守恒定律的研究对象是物体系统，是指系统的总机械能守恒，不是指某一个物体，单个物体无所谓机械能守恒。我们平时常说某物体的机械能守恒，只是一种习惯的说法，实际上应包括地球在内，因为物体的重力势能是物体与地球所共有的，而不是物体单独拥有的。系统的机械能是否守恒，选择研究对象很重要。

应用机械能守恒定律解题的一般步骤：

①选取系统对象，确定研究过程；

②进行受力分析，考察守恒条件；

③选取零势能平面，确定初、术态机械能；

④运用守恒定律，列方程求解。

应用机械能守恒定律解题的列式考虑角度：

①从守恒的角度列式——系统的初、末两状态机械能守恒，即E₂=E₂；

②从转化的角度列式——系统动能的增加等于势能的减少，即△E_k一-△E_p；

③从转移的角度列式

系统中一部分物体机械能的增加等于另一部分物体机械能的减少，即△E_a=-△E_B。

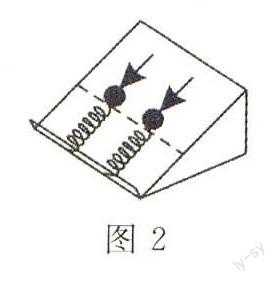
例2 （2014年高考福建卷第18题）如图2，两根相同的轻质弹簧，沿足够长的光滑斜面放置，下端固定在斜面底部的挡板上，斜面固定不动。质量不同、形状相同的两物块分别置于两弹簧上端。现用外力作用在物块上，使两弹簧具有相同的压缩量，若撤去外力后，两物块由静止沿斜面向上弹出并离开弹簧，则从撤去外力到物块速度第一次减为零的过程，两物块（）。

A.最大速度相同

B.最大加速度相同

C.升的最大高度不同

D.重力势能的变化量不同

当物块的加速度等于零，即kx=mgsinθ时，速度最大。因两物块质量m不同，故物块速度达最大时两弹簧的压缩量x不同，即两物块速度最大的位置不同，最大速度也就不同，A错。

在从撤去外力到物块速度第一次减小为零的过程中，对系统应用机械能守恒定律，有E_p=mgh。因初时两弹簧棚同且具有相同的压缩量，弹性势能E_p相同，而两物块质量m不同，故上升的最大高度h不同，C对。

系统的机械能守恒，物块重力势能的变化量△F_p'等于弹簧弹性势能的减少量△E_p而△E_p=E_p故△E_p'相同，D错。

本题正确选项为C。

本题涉及机械能守恒定律在直线运动中的应用，同时考查了牛顿第二定律。在应用机械能守恒定律求解问题时，研究对象与过程的选取尤为重要。本题中物块与弹簧各自的机械能并不守恒.系统的机械能才是守恒的；外力作用在物块上压缩弹簧的过程机械能并不守恒，撤去外力后系统的机械能才是守恒的。

例3 （201 2年高考全国理综大纲卷第26题）一探险队员在探险时遇到一山沟，山沟的一侧竖直，另一侧的坡面呈抛物线形状。该队员从山沟的竖直

（1）求此人落到坡面时的动能。

（2）此人水平跳出的速度为多大时，他落在坡面时的动能最小？动能的最小值为多少？

（1）设该队员在空中运动的时间为t，在坡而上落点的横坐标为x，纵坐标

本题涉及机械能守恒定律在平抛运动中的应用，确定探险队员跳下的高度是求解的关键。需要指出的是：应用机械能守恒定律处理平抛运动问题时，只能求得物体落地时的动能，进而求得物体落地速度的大小，而无法求出速度的方向。若要确定落地速度的方向，还得应用平抛运动的相关规律进行分析。

核心考点三：验证机械能守恒定律实验

通过研究物体自由下落的运动来验证机械能守恒定律，实验装置如图4所示。其实验原理是：忽略空气阻力，自由下落的物体在运动过程中机械能守恒，即动能的增加等于重力势能的减少。一般分两种情况加以验证：

例4 （2013年高考海南卷第1l题）某同学用图4所示的实验装置验证机械能守恒定律。已知打点计时器所用电源的频率为50Hz，当地重力加速度为g=9.80m/s2。实验中该同学得到的一条点迹清晰的完整纸带如图5所示。纸带上的第一个点记为O，另选连续的三个点A、B、C进行测量，图中给出了这三个点到O点的距离h_A、h_C和hc的值。

（2）通过分析该同学测量的实验数据，他的实验结果是否验证了机械能守恒定律？简要说明分析的依据。

本题利用重物的自由下落验证机械能守恒定律，考查同学们在理解实验原理、熟悉实验过程的基础上，处理实验数据并对实验结果作出正确判断的能力。

核心考点四：功能关系

功与能的定性关系：做功的过程是能量转化的过程，功是能量转化的量度。

力学中几种力的功与引起能量变化的定量关系：

①合外力做的功或外力做功的代数和等于物体或物体系统动能的变化，即∑W =△Ek（动能定理）。

②除重力和弹力外，其他力对物体系统做的功等于物体系统机械能的变化，即WF =△E（功能原理）。

③重力或弹力对物体做的功与重力势能或弹性势能的变化数值相等，即W_C=-△E_P或W_N=-△E_P'。

④两物体间滑动摩擦力对物体系统做的功与物体系统增加的内能数值相等，即W_f=Q。

功能原理与动能定理：由动能定理的表达式

例5 （2013年高考海南卷第13题）一质量m=0.6 kg的物体以v₀=20m/s的初速度从倾角为30。的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时，其动能减少了△E_k=18J，机械能减少了△=3J。不计空气阻力，重力加速度度g=10m/s2，求：

（1）物体向上运动时加速度的大小；

（2）物体返回斜坡底端时的动能。

（1）设物体在运动过程中所受的摩擦力大小为f，向上运动时的加速度大动能减少△E_k时，在斜坡上运动的距离为s，由动能定理或功能原理，有△E_k=（mgsinθ十f）s，△E=fs，解得a=6m/s2。

本题中物体与斜坡间有摩擦，所以物体在沿斜坡运动过程中机械能不守恒。当机械能不守恒时，往往可以考虑应用动能定理或功能原理加以分析求解。

跟踪训练：

1.（2015年江苏连云港、徐州、淮安、宿迁高三一模卷第13题）如图6，半径R=0.5 m的光滑圆弧轨道ABC与足够长的粗糙轨道CD在C处平滑连接，0为圆弧轨道ABC的圆心，B点为圆弧轨道的最低点，半径OA、OC与OB的夹角分别为53°和37°。将一个质量m=0.5kg的物体（可视为质点）从A点左侧高为h=0.8m处的P点水平抛出，恰从A点沿切线方向进入圆弧轨道。已知物体与轨道CD间的动摩擦因数μ=0.8，重力加速度g=10m/s2，sin 37°=0.6，cos37°一0.8。求：

（1）物体水平抛出时的初速度大小v。；

（2）物体经过B点时，对圆弧轨道的压力大小F_N；

（3）物体在轨道CD上运动的距离x。