揭开神秘的面纱 走进璀璨的殿堂

许长泰

摘   要：教师的授课，应该认真地把握好知识的节点，有的放矢地做好“导”的角色转变，特别是对于中等或中等以下的学生，教师的课堂教学角色尤显重要.

关键词：数学;解题;方法;研讨

学好数学其实一点都不难，一定要找到感觉，本文将着重从几个事例，来加以印证如何引领学生走进数学的殿堂，慢慢地揭开它的面纱.每道题都有它的构造特点，如何在细节上多下功夫，是解决问题的关键.因此，教师的授课，应该认真地把握好知识的节点，有的放矢地做好“导”的角色转变，特别是对于中等或中等以下的学生，教师的课堂教学角色很重要，应重视对问题的详细分析.

1   循序渐进，找回信心与感觉

有一天，一个学生问我这样一道题：已知+=2，则a的取值范围是____________.如果你滔滔不绝地讲下来，以后碰到了类似的题学生还是不会做，因为数学不是靠记或背来学的，而是要领悟其缘由，因此我借助于图1数形结合的思想来分析：+=|2-a|+|a-4|=2，然后在数轴上以2和4为界点进行分类讨论，此时中等生不太明确为什么要分成①a<2;②2≤a≤4;③a>4这三种情况来讨论？此时教师应该耐心地抓住知识的节点，要判断代数式2-a与a-4的取值符号，就得以2-a =0与a-4=0为界，因此将数轴分成三部分来讨论，即可得出a的取值范围是2≤a≤4.

2   解开层层迷雾

生活中处处布满迷团和叠障，只要我们勇敢地面对，即可拨开迷雾见青天.如何解决生活中的数学问题，也是如此，只要我们掌握恰当的数学学习方法 [1 ]，明确其数学的模型特点，层层深入，从容地找到解题的技巧，一切问题也就迎刃而解了.

例如：某学校开展“青少年科技创新比赛”活动，“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A，B同时出发，沿轨道到达C处，在AC上，甲的速度是乙的速度的1.5倍，设t（分）后甲、乙两遥控车与B处的距离分别为d1，d2（米），则d1，d2与t的函数关系如图2，试根据图象解决下列问题：

（1）填空：乙的速度v2=___________米/分;

（2）写出d1与t的函数关系式;

（3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？

分析：这是一道一次函数的应用题，“分类讨论”起到很大的作用，特别是第（3）小题，从图象中不难发现：（1）根据路程与时间的关系，可得答案：乙的速度v2=120÷3=40（米/分）.

（2）根据甲的速度是乙的速度的1.5倍，可得甲的速度，根据路程与时间的关系，可得a的值，根据待定系数法，可得答案：

v1=1.5v2=1.5×40=60（米/分），60÷60=1（分钟），a=1，因为甲、乙两遥控车都沿直线轨道AC做匀速直线运动，则

d1=-60t+60（0≤t<1）;60t-60（1≤t≤3）.

（3）根据两车的距离，可得不等式，根据解不等式，可得答案.

d2=40t，由辅助的平面行程图3可知当0≤t≤1时，两车的距离为d2+d1>10，即-60t+60+40t>10，解得t<2.5.

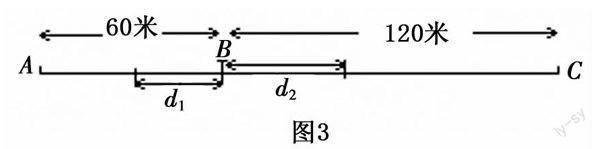
∴当0≤t<1时，两遥控车的信号不会产生相互干扰;

当1≤t≤3时，d2-d1>10，即40t-（60t-60）>10，

当1≤t<2.5时，两遥控车的信号不会产生相互干扰

综上所述：当0≤t<2.5时，两遥控车的信号不会产生相互干扰.

本题综合性地考查了一次函数的应用：（1）利用了路程速度时间三者的关系;（2）分段函数分别利用待定系数法来求解;（3）利用分类讨论的思想来解决，即当0≤t≤1时，d2+ d1>10;当110，分类讨论是解题关键.

从上述的解答中，我们可以发现，其实有很多数学问题都可以借助分类讨论的方法来解决，这就需要老师不断地培养学生的分析能力，解决问题的能力，加深领会数形结合的思想方法，发展学生形象思维能力 [2 ].

再例如：已知点B（0，3），C（0，1），对大于1的常数m，求x轴上的点M的坐标，使得sin∠BMC=.

分析：由于BC=2，sin∠BMC=，因此点M在以BC为弦，半径为m的⊙E上，因而点M应是⊙E与x轴的交点.然后对⊙E与x轴的位置关系进行讨论，只需运用矩形的判定定理与性质、勾股定理等知识就可求出满足要求的点M的坐标.

解：当1

∵CP是⊙E的直径，

∴∠PBC=90°.

∴sin∠BPC===

∵sin∠BMC=，

∴∠BMC=∠BPC.

∴点M在⊙E上.

∵点M在x轴上

∴点M是⊙E与x轴的交点.

∵EG⊥BC，

∴BG=GC=1.

∴OG=2.

∵∠EHO=∠GOH=∠OGE=90°，

∴四边形OGEH是矩形.

∴EH=OG=2，EG=OH.

∵1

∴EH>EC.

∴⊙E与x轴相离.

∴x轴上不存在点M，使得sin∠BMC=.

②当m=2时，EH=EC.

∴⊙E与x轴相切.

Ⅰ.切点在x轴的正半轴上时，如图5所示.

∴点M与点H重合.

∵EG⊥OG，GC=1，EC=m，

∴EG==.

∴OM=OH=EG=.

∴点M的坐标为（，0）.

Ⅱ.切点在x轴的负半轴上时，同理可得：点M的坐标为（-，0）.

③当m>2时，EH

Ⅰ.交点在x轴的正半轴上时，设交点为M、M′，连接EM，如图5所示.

∵∠EHM=90°，EM=m，EH=2，

∴MH===.

∵EH⊥MM′，∴MH=M′H.

∴M′H=.

∵∠EGC=90°，GC=1，EC=m，

∴EG===.

∴OH=EG=.

∴OM=OH-MH=-，

OM′=OH+HM′=+，

∴M（-，0）、

M′（+，0）.

Ⅱ.交点在x轴的负半轴上时，

同理可得：M（-+，0）、

M′（--，0）.

本题考查了用待定系数法求反比例函数的关系式、勾股定理、三角函数的定义、矩形的判定与性质、直线与圆的位置关系、垂径定理等知识，考查了用面积法求三角形的高，考查了通过构造辅助圆解决问题，综合性比较强，难度较大.由BC=2，sin∠BMC=联想到点M在以BC为弦，半径为m的⊙E上是解决本题的关键.如何引导学生构建辅助圆的模型及分类讨论的方法呢？首先要求的点M在x轴上，而∠BMC可想像以BC为公共弦的同弧圆周角，因此所构造的⊙E的半径为m，CE交⊙E于点P，连BP，则∠PBC=90°，故sin∠BMC= sin∠BPC===;模型构造完后，再进一步地往下探究，不难发现，随着m取值的变化，⊙E与x轴的交点情况也将随之改变，因此接下来将逐一讨论⊙E与x轴相离、相切和相交这三种情况，当然还得考虑⊙E落在y轴左侧时的情形，只要利用对称性即可得出完整的答案.

3   找到解决问题的关键

作为教师，面对的是一群懵懂的学生.为了让每一个学生都能得到不同的发展，教师要适时点拔，给学生自主探究空间，掌握发现问题、分析问题的方法，最终达到具备解决问题的能力.

下面我们再来探究函数图像平移与分类问题：

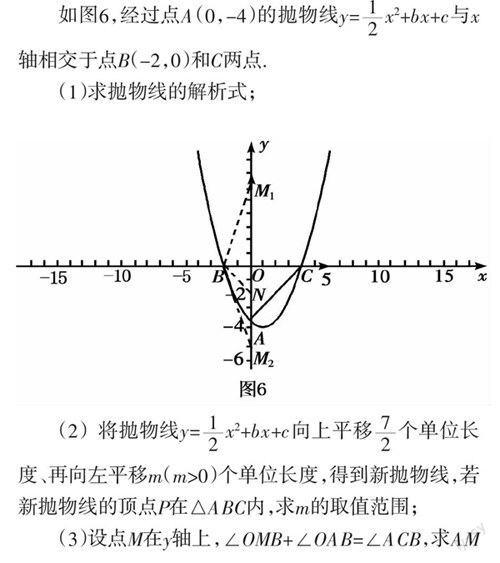
如图6，经过点A（0，-4）的抛物线y=x2+bx+c与x轴相交于点B（-2，0）和C两点.

（1）求抛物线的解析式;

（2）将抛物线y=x2+bx+c向上平移个单位长度、再向左平移m（m>0）个单位长度，得到新抛物线，若新抛物线的顶点P在△ABC内，求m的取值范围;

（3）设点M在y轴上，∠OMB+∠OAB=∠ACB，求AM的长.

分析：（1）将点A、B代入抛物线即可得抛物线的解析式为：y=x2-x-4.

（2）依题意，得y=（x+m-1）2-1∴顶点P（1-m，-1），由（1）抛物线的解析式得C（4，0）.

因此直线AB：y=-2x-4; 直线AC：y=x-4.

当点P在直线AB上时，-2（1- m）-4=-1，解得m=2.5;

当点P在直线AC上时，（1- m）-4=-1，解得m=-2.

∴当点P在△ABC内时，-2

又∵m>0，则符合条件的m的取值为：0

（3）由A（0，-4），B（-2，0）得AO=OC=4，且△OAC为等腰直角三角形.

如图在OA上取ON=OB=2，则∠ONB=∠ACB=45°.

∴∠ONB=∠NBA+∠OAB=∠ACB=∠OMB+∠OAB，即∠NBA=∠OMB.

如图，在△ABN，△AMB中，∠BAN=∠M1AB，∠ABN=∠AM1B.

∴△ABN∽△AM1B，得AB2=AN·AM1 .

易得：AM1==10.OM1= AM1-OA=10-4=6，而∠AM1B=∠AM1B=∠ABN，

∴OM1=OM1=6，AM1=OM1-OA=6-4=2.

综上：AM的长为10或2.

通过本题的分析，我们容易发现，学好数学并不难，只要我们能利用数形结合的思想方法，能耐心地揣摩出题中条件的意图，即使题中需要分类讨论也可以逐一地解开它的面纱.

本文通过几个与分类讨论有关的范例，让学生掌握分类思想在具体问题中的应用条件、方式增添了学好数学的信心，因本人阅力有限，才疏学浅，表述上若有不妥之处，请广大读者能提出批评指正.

参考文献：

[1]程银生.一道被舍弃填空题的教学运用[J]. 中学数学教学参考，2014（6）：41-43.

[2]赵立春. “一次函数模型的应用”难点剖析及教法改进[J].中学数学教学参考，2015（1-2）：39.