谈中考数学的情境应用问题

林永金 林晴岚

摘   要：情境应用问题以现实生活为背景，取材新颖，立意巧妙，旨在考查阅读理解能力和数学建模能力，让学生在阅读理解的基础上，将实际问题抽象转化为数学问题.解决这些应用问题，关键是审题，弄清关键的词句及含义;重点是分析，找出问题中的数量关系，并将其转化为数学式子，进行整理、运算、解答.

关键词：中考;数学;情境;应用

新课程要求把学生的发展作为教学的出发点.因此，数学教学活动必须建立在学生的认知发展水平和已有的知识经验及生活经验的基础上，教学活动的素材应有利于激发学生的学习积极性.情境应用问题以现实生活为背景，取材新颖，立意巧妙，旨在考查阅读理解能力和数学建模能力，让学生在阅读理解的基础上，将实际问题抽象转化为数学问题.

建构主义理论认为学习数学是主体对数学知识的认识过程，学生的数学学习活动不应只限于接受、记忆、模仿、练习等被动的吸收过程，而应是在教师指导下依赖于已有的认知结构而进行的主动建构学习的过程.情境应用问题主要类型包括不等式型，方程型，函数型，统计型四大类，解决这些应用问题，关键是审题，弄清关键的词句及含义;重点是分析，找出问题中的数量关系，并将其转化为数学式子，进行整理、运算、解答.下面以近几年龙岩市数学中考题为例，谈谈情境应用问题.

1   方程型情境应用题

方程（组）模型是刻画现实世界数量关系的最基本的数学模型，它可以通过数量关系准确地揭示问题的本质.

例1   已知：用2辆A型车和1辆B型车装满货物一次可运货10吨; 用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都装满货物.

根据以上信息，解答下列问题：

（1）1辆A型车和1辆B型车都装满货物一次可分别运货多少吨？

（2）请你帮该物流公司设计租车方案;

（3）若A型车每辆需租金100元/次，B型车每辆需租金120元/次.请选出最省钱的租车方案，并求出最少租车费.

解：（1）设1辆A型车、1辆B型车都装满货物一次可分别运货x吨、y吨，依题意列方程组得：

2x+y=10x+2y=11 ，解方程组，得x=3y=4 .

答：1辆A型车装满货物一次可运3吨，1辆B型车装满货物一次可运4吨.

（2）结合题意和（1）得3a+4b=31，

∴a=.

∵a、b都是正整数，

∴a=9b=1， 或a=5b=4， 或a=1b=7 .

答：有3种租车方案： ①A型车9辆，B型车1辆;

②A型车5辆，B型车4辆;

③A型车1辆，B型车7辆.

（3） 方案 ①需租金：9×100+120=1020（元）;

方案 ②需租金：5×100+4×120=980（元）;

方案 ③需租金：1×100+7×120=940（元）.

∵  1020>980>940，

∴  最省钱的租车方案是：

A型车1辆，B型车7辆，最少租车费为940元.

点评：方程（组）型应用题是指应用题的背景材料可以转化为方程（组）模型来解决的题目，解决这类问题的关键是针对背景材料，设定合适的未知数，找出相等关系，建立方程（组）模型.

2   不等式型情境应用题

不等式（组）型应用题是指应用题的背景材料可以转化为不等式（组）来解决的题目，解决这类问题的关键是针对背景材料，确定某个量的变化范围，建立不等式（组）模型，列不等式解应用题.

例2   龙岩市某中学2013届九年级（1）班学生为四川雅安灾区人民开展募捐活动，募捐活动共收得募捐款2200元.班委会决定拿出不少于850元但不超过900元的募捐款直接汇给灾区红十字会，其余募捐款直接用于为灾区某校九年级（1）班50名同学每人购买一个文具盒或一个书包，并邮寄给他们，假定邮费共计30元;已知每个书包的单价比每个文具盒多12元，用176元恰好可以买到4个文具盒和3个书包.

（1）求每个文具盒和每个书包的价格分别为多少元;

（2）有几种购买文具盒和书包的方案？

解：（1）设1个文具盒的单价为x元，则1个书包单价为（x+12）元.

依题意，得：4x+3（x+12）=176，

解得x=20，所以x+12=32，

所以，书包每个32元，文具盒每个20元 .

（2）设购买文具盒y个，则购买书包（50-y）个.

依题意，得：20y+32（50-y）≥2200-900-3020y+32（50-y）≤2200-850-30 ，

解得23≤y≤27，

∵y是整数  ∴ y取24、25、26、27.

所以，有四种购买方案：

购买文具盒24个，书包26个

购买文具盒25个，书包25个

购买文具盒26个，书包24个

购买文具盒27个，书包23个.

点评：一般所求问题中有“至少”、“最多”、“不低于”、“不大于”、“不小于”、“高于”等词，要正确理解这些词的含义，同时，在最后确定未知数的值时要注意未知数所表示的实际意义，通常取正整数值.

3   函数型情境应用题

“关注课标， 贴近生活，联系实际”是中考函数应用题的编题原则，包括一次函数、反比例函数、二次函数及函数图象信息方面的应用.

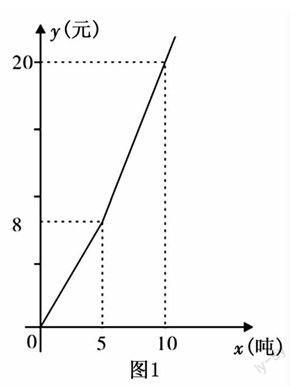
例3   随着地球上的水资源日益枯竭，各级政府越来越重视倡导节约用水.某市对居民生活用水按“阶梯水价”方式进行收费，人均月生活用水收费标准如图1所示.图中x表示人均月生活用水的吨数，y表示收取的人均月生活用水费（元）.请根据图象信息，回答下列问题：

（1）该市人均月生活用水的收费标准是：不超过5吨，每吨按      元收取;超过5吨的部分，每吨按      元收取;

（2）请写出y与x的函数关系式;

（3）若某个家庭有5人，五月份的生活用水费共76元，则该家庭这个月用了多少吨生活用水？

解：（1）1.6，2.4;

（2）y=x（0≤x≤5）x-4（x>5）;

（3）∵5个人五月份的生活用水费是76元，

∴平均每个人的生活用水费是元，

∵>8，

∴x-4=，

解得，x=8.

∴5×8=40（吨）.

答：该家庭这个月共用了40吨生活用水.

点评：解决此类问题的关键是学会用数学知识去观察、分析、概括所给的实际问题，将其转化为函数模型.

4   统计型情境应用题

统计型应用题是指利用统计知识来解决的应用题，这类问题选材紧密联系生活实际，关注社会热点，注重背景设置的新颖性.

例4   某校九年级有10个班，每班50名学生.为调查该校九年级学生一学期课外书籍的阅读情况，准备抽取50名学生作为一个样本进行分析，并规定如下：设一个学生一学期阅读课外书籍本数为n，当0≤n<5时为一般读者;当5≤n<10时为良好读者;当n≥10时为优秀读者.

（1）下列四种抽取方法最具有代表性的是         ;

A.随机抽取一个班的学生  B.随机抽取50名学生

C.随机抽取50名男生         D.随机抽取50名女生

（2）由上述最具代表性的抽取方法所抽取50名学生一学期阅读本数的数据如下：

根据以上数据回答下列问题：

①求样本中优秀读者的频率;

②估计该校九年级优秀读者的人数;

③在样本为一般读者的学生中随机抽取2人，用树形图或列表法求抽得2人的课外书籍阅读本数都为4的概率.

解：（1） B ;

（2）①=， ∴优秀读者的频率是;

② 500×=200（人），∴估计该校九年级优秀读者有200人;

③列树形图如图2：

由树形图可知，共有16种情况，其中每种情况的可能性相同.其中两个都为4的情况有4种，

∴P（都为4）==

点评：解决此类题目的一般思路是收集信息，然后整理、描述、分析数据解决实际问题.