在问题解决中绽放思考的魅力
陈冬华
[摘要]数学课程的教学,不能仅仅让学生的思维停留于简单的知识积累,满足于运用某一方法获得某一问题的正解上,更重要的是让学生的思考绽放无限的魅力,从而培养学生的思维能力,有效提升学生的数学素养.
[关键词]问题解决思维提升生成经验
[中图分类号]G633.6[文献标识码]A[文章编号]16746058(2015)230024
前苏联教育家苏霍姆林斯基说:“在学生的脑力劳动中,摆在第一位的并不是背书,不是记住别人的思想,而是让学生本人进行思考.”在实际的数学课堂教学中,我围绕我校“问题导学灵动课堂”课题,带着学生经历探究、思考、猜想、验证、反思等学习过程,有效培养了学生的思维能力.
一、享受思考,在无拘无束中放飞思维
数学教学的价值,不仅在于学生识记几个公式、掌握几种解题技巧,而在于让学生学会有效思考问题、真正解决问题并形成终身学习的能力.教师应认真研究教学内容,精心设计教学过程,让学生在有限的课堂时空里最大限度地享受思考的乐趣,于放飞思维中形成能力.
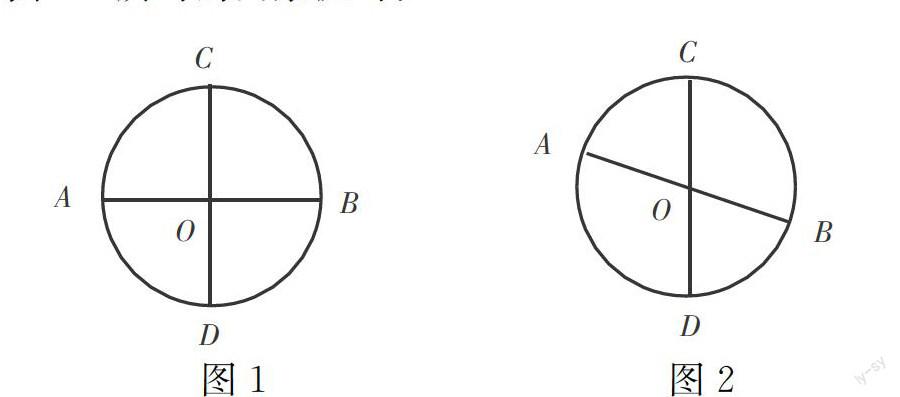
例如,教学《垂直于弦的直径》时,在课堂的一开始,我设计了如下问题串,引导学生全面、深刻地思考:(1)你能用折纸的方法确定圆形纸片圆心的位置吗?动手试一试!(2)在折叠圆的过程中,你发现圆是怎样的一个对称图形?(3)在图1、图2两幅图中,两条直径分别有什么关系?(4)在图1中,两条互相垂直的直径AB、CD,直径CD不动,直径AB向下平移,变成一条普通的弦,并且仍保持CD⊥AB,图中有哪些相等的线段和弧?为什么?(5)在图2中,直径AB、CD互相平分但不垂直;若向下平移AB,直径CD、弦AB什么关系?旋转圆使直径CD经过弦AB的中点E,CD⊥AB吗?CD还平分弦AB所对的两条弧吗?
图1图2
我用这些由浅入深、有思考性的问题来引导学生探究知识,充分发挥了学生的主体作用,激发了学生的求知欲,发展和提升了学生的思维能力.
二、生成经验,在合作探究中形成策略
在学生经历了在原有经验基础上的有序思考后,我们继续引领他们合作探究、思考、操作,培养他们全面思考问题的意识与能力.这一过程中,同一小组内原先已有基础不同、认识经验不同的成员,都会有意识或无意识地反思自己刚才的思考,借鉴、迁移他人的合理发现,主动完善自己的认知结构,并逐步内化成自己的东西,形成解决问题的策略.同时,他们在活动中更积累了宝贵的思考经验和丰富的操作活动经验,这对培养学生良好的数学素养大有裨益.
例如,教学《垂直于弦的直径》时,我针对中考的常见题型,在学生基本理解和掌握了“垂径定理及其推论”的基础上,设计了这样一个问题:赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?展示这个问题后,学生先独立思考,然后小组交流与合作学习,最后全班进行展示、评价、完善.学生在合作探究中总结出了最佳解题策略.
对于这类能激发学生探究欲望、有探究价值、有合作必要的问题,教师可大胆放手,在生生合作、师生合作的多向互动中充分发挥学生的主体作用,使学生在思维碰撞中获得宝贵的经验,从而实现课堂教学目标.
三、完善提升,在科学建构中提升素养
对于学生在自我思考、合作探究中逐步完善的新认知,教师还要引导学生加以概括、归纳、反思,并进行巩固和拓展,使学生的思维上升为带着学生个体认识色彩而又达成共识的严谨思维.这样的精心收官,可促进学生加深知识印象、严谨表达、提升素养.
例如,教学《垂直于弦的直径》时,在课堂的后一阶段,一方面,我通过问题“你有什么收获与体会”引导学生从自己的认知和感悟出发,从圆的对称性、垂径定理的内容及其证明方法、垂径定理的应用等方面进行反思、总结;另一方面,我针对教学内容,设计了一系列的问题,让学生在变式中提升能力.如根据练习“在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径”引出变式:①在⊙O中,⊙O的半径为5cm,圆心O到AB的距离为3cm,求弦AB的长;②在⊙O中,⊙O的半径为5cm,弦AB的长为8cm,求圆心O到弦AB的距离;③在⊙O中,弦AB的长为8cm,半径OC⊥AB,垂足为D,若CD的长为2cm,求⊙O的半径.
通过引导学生对问题解决过程的反思,使学生对现有的知识进行巩固、拓展与延伸,夯实基础;通过例题验证、变式训练,让学生学会举一反三,使其在理解、体验、感悟中生成新的知识,提升学生的数学素养.
总之,在初中数学课堂中,教师应以“问题解决”为基石,以培养学生的思维能力为核心,以学生的成长为根本,在发现问题、解决问题的过程中,在师生、生生的互动中,促成学生自主归纳、自我提升.让数学课堂在问题解决中绽放思考的魅力!
(责任编辑钟伟芳)

