如何讲解连续信号频谱与离散信号频谱的关系

杨忠林 侯新国 欧阳华

【摘要】连续信号频谱与离散信号频谱的关系是“数字信号处理”、“信号与系统”等课程的重点和难点之一，本文分析了连续信号转化为离散信号的过程，并在此基础上，推到了连续信号频谱与离散信号频谱的关系，降低了学生理解的难度，提高了教学质量，取得了较好的教学效果。

【关键词】连续信号  离散信号  频谱  数字信号处理

【Abstract】 The relationship between the continuous signal spectrum and the discrete signal spectrum is the one of the important and difficult points in “Digital Signal Processing” course and “Signals and Systems” course. In this paper， the transformation process from the continuous signals into the discrete signal was analyzed. And on this basis， the relationship between the continuous signal spectrum and the discrete signal spectrum was deduced， which reduce the difficulty of understanding of students and improve the quality of teaching， so good teaching effect was achieved.

【Keywords】 Continuous Signal; Discrete Signal; Spectrum; Digital Signal Processing

【中图分类号】G64 【文献标识码】A 【文章编号】2095-3089（2015）08-0209-02

离散信号可以由连续信号经过采样得到[1-4]，而这两者之间的关系是在《信号与系统》、《数字信号处理》等课程中非常重要的内容，然而学生往往难以理解连续信号频谱与离散信号频谱的关系。本文通过分析连续信号转化为离散信号的过程，推导每一步信号频谱的变换过程，使得学生容易理解两者频谱的关系。

一、连续信号离散化的过程

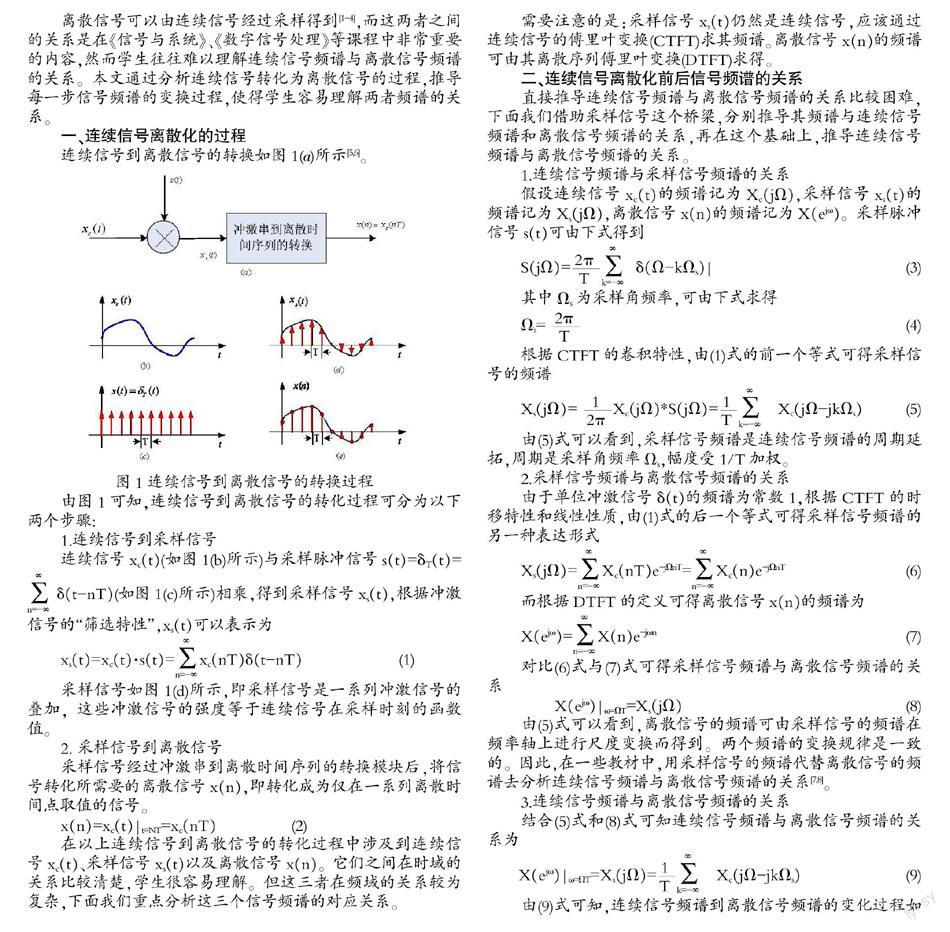
连续信号到离散信号的转换如图1（a）所示[5，6]。

图1 连续信号到离散信号的转换过程

由图1可知，连续信号到离散信号的转化过程可分为以下两个步骤：

1.连续信号到采样信号

连续信号xc（t）（如图1（b）所示）与采样脉冲信号s（t）=δT（t）=■ δ（t-nT）（如图1（c）所示）相乘，得到采样信号xs（t），根据冲激信号的“筛选特性”，xs（t）可以表示为

xs（t）=xc（t）·s（t）=■xc（nT）δ（t-nT）                  （1）

采样信号如图1（d）所示，即采样信号是一系列冲激信号的叠加，这些冲激信号的强度等于连续信号在采样时刻的函数值。

2. 采样信号到离散信号

采样信号经过冲激串到离散时间序列的转换模块后，将信号转化所需要的离散信号x（n），即轉化成为仅在一系列离散时间点取值的信号。

x（n）=xc（t）|t=NT=xc（nT）              （2）

在以上连续信号到离散信号的转化过程中涉及到连续信号xc（t）、采样信号xs（t）以及离散信号x（n）。它们之间在时域的关系比较清楚，学生很容易理解。但这三者在频域的关系较为复杂，下面我们重点分析这三个信号频谱的对应关系。

需要注意的是：采样信号xs（t）仍然是连续信号，应该通过连续信号的傅里叶变换（CTFT）求其频谱。离散信号x（n）的频谱可由其离散序列傅里叶变换（DTFT）求得。

二、连续信号离散化前后信号频谱的关系

直接推导连续信号频谱与离散信号频谱的关系比较困难，下面我们借助采样信号这个桥梁，分别推导其频谱与连续信号频谱和离散信号频谱的关系，再在这个基础上，推导连续信号频谱与离散信号频谱的关系。

1.连续信号频谱与采样信号频谱的关系

假设连续信号xc（t）的频谱记为Xc（jΩ），采样信号xs（t）的频谱记为Xs（jΩ），离散信号x（n）的频谱记为X（ejω）。采样脉冲信号s（t）可由下式得到

S（jΩ）=■■  δ（Ω-kΩs）|                 （3）

其中Ωs为采样角频率，可由下式求得

Ωs= ■                         （4）

根据CTFT的卷积特性，由（1）式的前一个等式可得采样信号的频谱

Xs（jΩ）= ■Xc（jΩ）*S（jΩ）=■■   Xc（jΩ-jkΩs）     （5）

由（5）式可以看到，采样信号频谱是连续信号频谱的周期延拓，周期是采样角频率Ωs，幅度受1/T加权。

2.采样信号频谱与离散信号频谱的关系

由于单位冲激信号δ（t）的频谱为常数1，根据CTFT的时移特性和线性性质，由（1）式的后一个等式可得采样信号频谱的另一种表达形式

Xs（jΩ）=■Xc（nT）e-jΩnT=■Xc（n）e-jΩnT              （6）

而根据DTFT的定义可得离散信号x（n）的频谱为

X（ejω）=■X（n）e-jωn                     （7）

对比（6）式与（7）式可得采样信号频谱与离散信号频谱的关系

X（ejω）|ω=ΩT=Xs（jΩ）                   （8）

由（5）式可以看到，离散信号的频谱可由采样信号的频谱在频率轴上进行尺度变换而得到。两个频谱的变换规律是一致的。因此，在一些教材中，用采样信号的频谱代替离散信号的频谱去分析连续信号频谱与离散信号频谱的关系[7，8]。

3.连续信号频谱与离散信号频谱的关系

结合（5）式和（8）式可知连续信号频谱与离散信号频谱的关系为

X（ejω）|ω=ΩT=Xs（jΩ）=■■   Xc（jΩ-jkΩs）             （9）

由（9）式可知，连续信号频谱到离散信号频谱的变化过程如图2所示。这个过程可以分为两步：首先，对连续信号的频谱进行周期延拓，得到采样信号的频谱;其次，在对采样信号的频谱在频率轴上进行尺度变换，得离散信号的频谱。

图2 连续信号频谱到离散信号频谱的变化过程

三、模拟频率与数字频率的关系

前面的过程不仅推导了连续信号频谱与离散信号频谱的关系，而且推导了模拟频率Ω与数字频率ω的关系。由（8）式可知连续频率与离散频率的关系为

ω=ΩT=2π■                          （10）

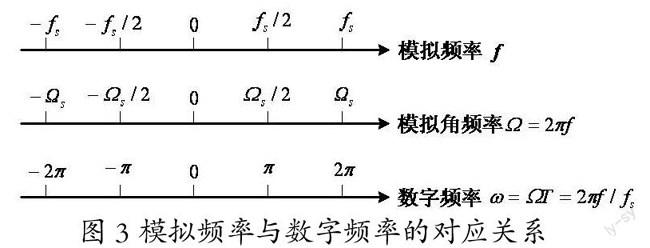
由（10）可知，模拟频率Ω与数字频率ω之间具有线性关系，数字频率是模拟频率对采样频率的归一化值，它代表了离散信号值变化的速率。所以它只有相对的时间意义（相对于采样周期T），而没有絕对时间和频率的意义。模拟频率f、模拟角频率Ω以及数字频率ω的对应关系如图3所示。

图3 模拟频率与数字频率的对应关系

四、结论

在《数字信号处理》、《信号与系统》等课程中，连续信号频谱与离散信号频谱的关系是一个非常重要的知识点，本文根据连续信号到离散信号的转化过程，借助采样信号这桥梁，详细推到了连续信号频谱与离散信号频谱的关系，并同时推导了模拟频率Ω与数字频率ω的关系，使得学生对于连续信号到离散信号的转化过程中，信号频谱的变化规律有了更加直观的理解，取得了较好的教学效果。

参考文献：

[1]程佩青. 数字信号处理教程（第三版）[M]，北京：清华大学出版社，2007.

[2]尹为民，欧阳华，钱美. 数字信号处理[M]，北京：机械工业出版社，2011.

[3]Sanjit K Mitra. 数字信号处理-基于计算机的方法[M]，北京：电子工业出版社，2006.

[4]管致中，夏恭恪，孟桥. 信号与线性系统处理（第五版）[M]，北京：高等教育出版社，2011.

[5]A. V. 奥本海姆著，刘树棠，黄建国译. 离散时间信号处理（第二版）[M]，西安：西安交通大学出版社，2002.

[6]A. V. 奥本海姆著，刘树棠译. 信号与系统化（第二版）[M]，西安：西安交通大学出版社，2003.

[7]邵英. 信号与系统[M]，北京：国防工业出版社，2014.

[8]吴大正. 信号与线性系统分析（第四版） [M]，北京：高等教育出版社，2005.