大功率光伏逆变电抗器损耗分析与优化设计

陈媛冰，董纪清，陈为，洪添丁

(福州大学电气工程与自动化学院，福建 福州 350116)

1 引言

随着能源和环境问题的日益突出，作为一种取之不尽用之不竭的绿色能源，光伏发电越来越受到世界各国的关注，并在各国政府的支持下得到快速发展。

三相光伏逆变器的主电路拓扑如图1所示。由图中可以看出，逆变器的主电路主要包括直流母线电容，IGBT、滤波电容及滤波电抗器，这些元件均会产生损耗，直接影响光伏逆变系统的效率。目前，国内外学者对光伏逆变器损耗的研究主要集中在开关器件的损耗方面，并提出了相对成熟的开关损耗模型［1，2］。然而，除了IGBT的损耗外，滤波电抗器的损耗占光伏逆变器总损耗的比重也很大，对光伏逆变器的效率和性能有很大影响。因此，对电抗器损耗的分析研究对提高光伏逆变器的效率具有重要意义。本文通过对光伏逆变电抗器的损耗进行详细分析，并结合逆变器其它部分的损耗，以得到最高欧洲效率为目的优化设计电抗器的参数，使光伏逆变器的优化设计更加完善。

图1 三相光伏逆变器主电路图

对磁性元件损耗模型的分析、计算和设计，国内外专家学者已经开展了许多研究工作，并取得了大量成果。在铁芯损耗模型研究方面，Bettori在文献［3］中提出将铁芯损耗分成磁滞损耗、涡流损耗和杂散损耗三个方面的损耗模型。该方法较适合做理论分析和计算，工程上并不适用。目前应用最广泛的铁芯损耗模型是由C.P.Steinmetz提出的Steinmetz-equation，但该方法只适用于正弦激励下的铁芯损耗计算，且在不同频率段系数也有差别［4］。对于非正弦激励下的铁芯损耗计算，文献［5］提出将励磁波进行傅立叶分解后损耗叠加的方法，但由于铁芯损耗的非线性，该方法只能做粗略计算;文献［6，7］则提出修正的Steinmetz公式(MSE)以计算任意波形激励下的铁芯损耗。在绕组损耗模型研究方面，文献［8］介绍了由著名学者P.L.Dowell提出的Dowell一维模型，该模型把各种形式的绕组层转变成等效的铝箔，再用相对简单的一维分析方法对磁性元件的绕组损耗进行研究。

光伏逆变系统负载随着时间和天气的变化而变化，因此在分析电抗器损耗时要充分考虑不同的负载情况。此外，光伏逆变电抗器工作时不仅要通过基波大电流，还要承受开关器件的高频电流纹波，这也给电抗器的损耗分析增加了难度。本文通过对一个容量为500kVA的三相光伏逆变器LCL型电抗器进行损耗分析，充分考虑了不同负载状态下逆变器各部分的损耗，优化设计电抗器的参数，从而得到最优的欧洲效率。其中，接于逆变器侧的电感L1=0.1mH，接于并网侧的电感L2=0.05mH。对于LCL型滤波电抗器，由于输出滤波电容的作用，流过L2的高频电流纹波很小，仅考虑L1的高频电流谐波。因此，本文仅对电抗器L1的损耗进行分析，电抗器L2损耗的分析原理与之相同。流过电抗器L1的基波电流峰值为Im0=1555A，f=50Hz，谐波电流峰值为 Imh=130A，f=6kHz。电抗器的铁芯材料为23ZH90材质的硅钢片。

2 绕组损耗分析

2.1 绕组损耗一维模型

光伏逆变电抗器工作时需要通过大电流，因此绕组一般采用铜箔或铝箔绕制，本文分析的电抗器绕组采用铝箔绕制。由于光伏逆变电抗器铁芯需开气隙，气隙扩散磁通会在绕组上感应涡流从而产生一定的损耗，因此光伏逆变电抗器在设计时铁芯一般采用分布气隙的方式以减小气隙扩散磁通产生的附加损耗［9］。分布气隙的段数越多，气隙扩散磁通的影响也越小。当绕组与气隙之间的距离在3～5倍气隙长度以上，由气隙扩散磁通产生的附加损耗很小，可以忽略不计［10］。本文中电抗器L1铁芯的分布气隙段数为16段，气隙长度为1.4mm，绕组与气隙间的最小距离为8mm，大于气隙长度的5倍，因此本文忽略气隙扩散磁通产生的附加损耗。忽略气隙扩散磁通的影响后，正弦激励下的绕组损耗模型可以近似等效为一维涡流理论模型，其电流密度表达式为:

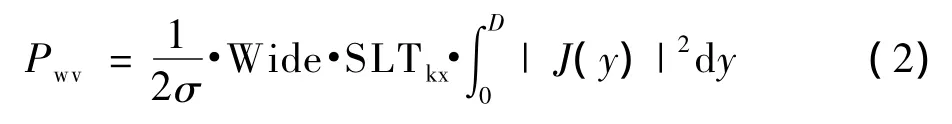
其中，Wide是铝箔的宽度，SLTkx是第kx匝绕组的长度。由于每一匝绕组的长度不同，因此在计算绕组损耗时需要计算出每匝绕组的长度。电抗器中柱和绕组的水平截面图如图3所示，其中，圆弧的半径可以由公式(3)计算得到。第kx匝绕组的长度可以近似表示为公式(4)所示:

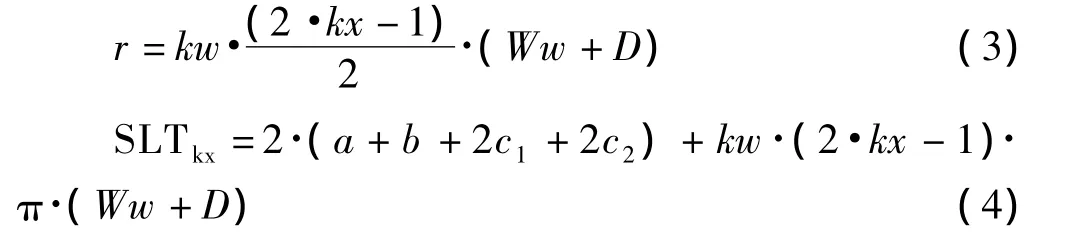
根据公式(2)和公式(4)可以得到绕组损耗的表达式为:

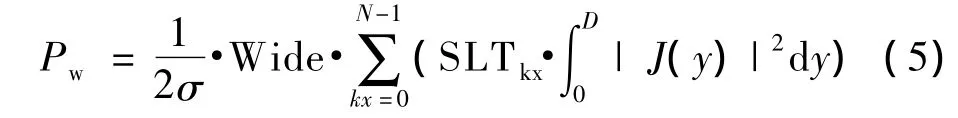
由于流过电抗器L1的电流除了含有基波分量外还含有高频谐波分量，属于非正弦周期函数，因此计算绕组损耗时需要先对电流进行傅立叶分解，再计算基波和各次谐波所对应的绕组损耗之和，从而得到总的绕组损耗为:

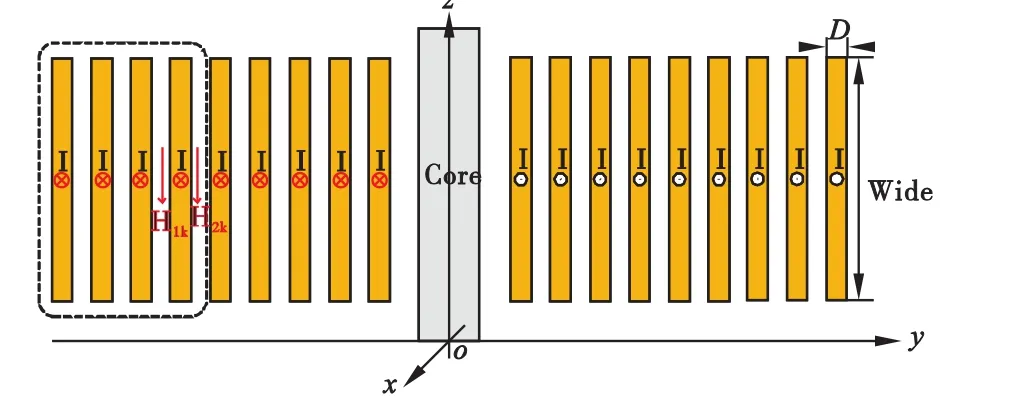
图2 绕组等效一维模型

2.2 绕组损耗优化

由公式(1)和公式(5)可以看出，在电流一定的情况下，绕组损耗与铝箔的匝数和厚度相关。图4表示满载时绕组的基波损耗、谐波损耗和总损耗与铝箔匝数和厚度的关系。从图中可以看出，在频率和铝箔厚度一定时，铝箔匝数越多，绕组损耗越大。当频率与匝数一定时，基波损耗随着铝箔厚度的增加而减少，谐波损耗随着铝箔厚度的增加而增加，绕组总损耗则随着铝箔厚度的增加呈现先减小后增大的趋势。因此，存在一个最优的铝箔匝数和厚度使绕组的总损耗最小。

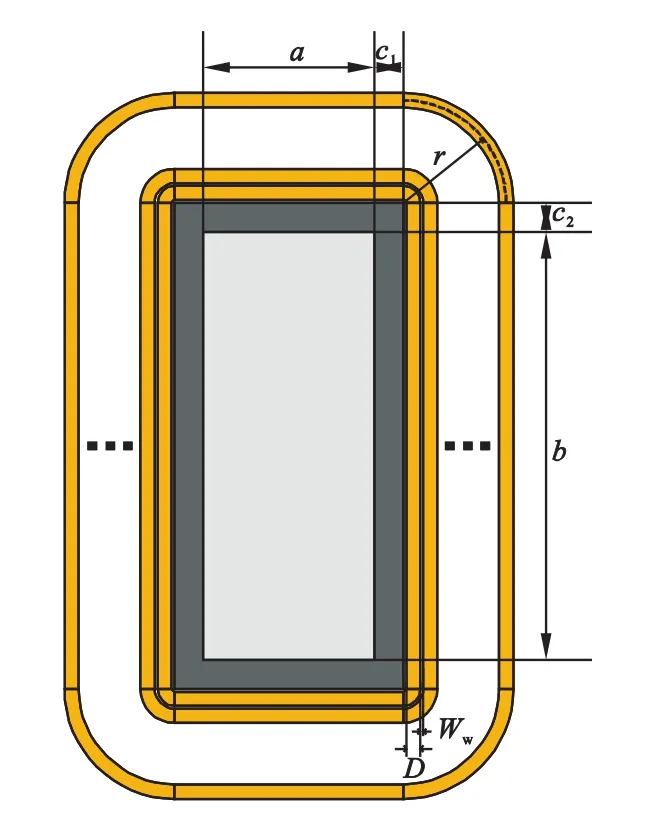
图3 电抗器中柱和绕组水平截面图

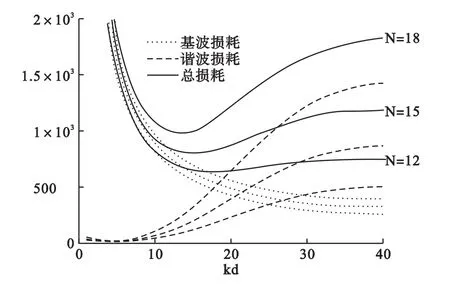
图4 满载下绕组损耗与铝箔匝数和厚度关系图

在不同负载下，绕组总损耗与铝箔匝数和厚度的关系如图5所示。从图中可以看出，不同负载所对应的绕组总损耗不同，负载越大，绕组总损耗也越大。每一个负载下都会对应不同的使绕组总损耗最小的铝箔匝数和厚度。

3 铁芯损耗分析

3.1 正弦激励下铁芯损耗曲线拟合

本文选用的电抗器铁芯材料为23ZH90材质的硅钢片。对于正弦激励下的铁芯损耗，目前工程中比较常用的单位铁芯损耗公式为Steinmetz公式，其表达式为:

图5 不同负载下绕组总损耗与铝箔匝数厚度关系图

该表达式可以根据硅钢片数据手册中的Bm－Pcv曲线拟合得到。根据不同频率下的Bm－Pcv曲线，取其中两条曲线中不共线的三个点(Bm1，f1，Pcv1)、(Bm2，f2，Pcv2)、(Bm3，f3，Pcv3)，代入公式(7)可以解得待定系数Cm、α和β值，从而拟合出对应频率段的铁芯损耗曲线公式，拟合出的损耗曲线可以由分段函数表示:

根据拟合的损耗曲线函数，可以画出工频和对应谐波频率下23ZH90的损耗特性曲线如图6所示。

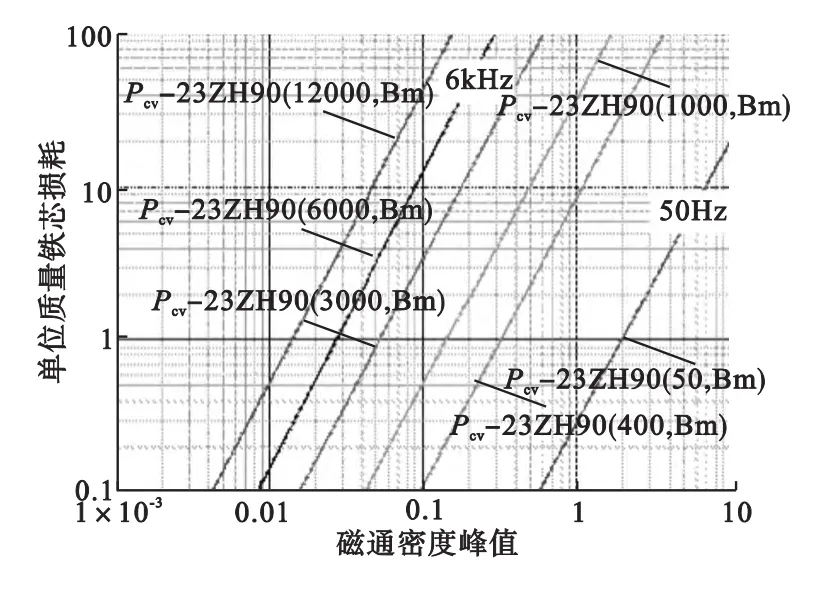
图6 铁芯损耗拟合曲线

3.2 任意波形激励下铁芯损耗计算

光伏逆变电抗器工作时，流过电抗器的电流是非正弦波。本文设计的电抗器感量和铁芯尺寸确定，根据磁通密度的计算公式，如公式(9)所示，可以得出单相磁通密度的曲线如图7所示，从图中可以看出，磁通密度也为非正弦波。对于非正弦激励下的铁芯损耗，本文采用修正的斯坦麦茨方程(MSE)进行计算。MSE方程采用磁密加权平均变化率的思想，即认为在相同的交流磁密下，如果两种励磁波形下的磁密加权平均变化率相同，则它们在一个周期内产生的磁芯损耗就相同，因此可以建立频率为f_ab的任意励磁波形下磁芯损耗与频率为fsin_eq的正弦波形励磁下磁芯损耗的等效关系，等效正弦波频率的计算如公式(10)所示。将等效正弦波频率代入Steinmetz公式得出非正弦激励下单位铁芯损耗表达式如公式(11)所示。本文先将磁通密度分为i段再将根据公式(10)和公式(11)分别计算每一段的单位铁芯损耗，积分后可算得电抗器的单位铁芯损耗。不同负载下单位铁芯损耗与铝箔匝数的关系如图8所示。从图中可以看出，单位铁芯损耗与铝箔匝数成反比，与负载的大小成正比。

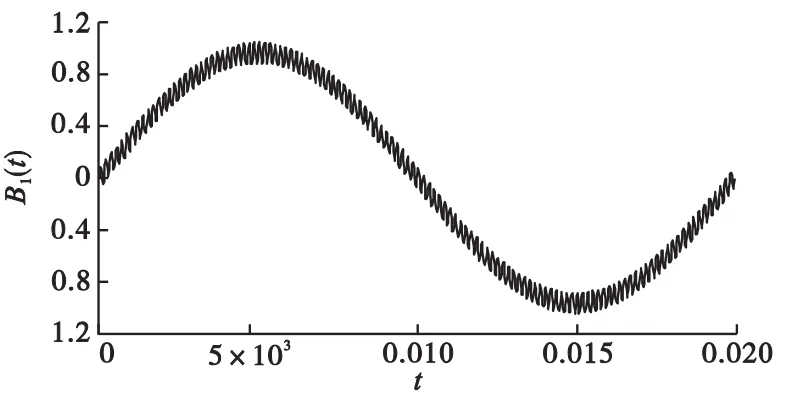
图7 磁通密度波形

图8 不同负载下铁芯损耗与铝箔匝数关系

4 欧洲效率优化设计

由于光伏逆变器负载随着天气和时间的变化而变化，其效率也随之改变，因此本文基于光伏逆变器的欧洲效率对电抗器的参数进行优化设计。欧洲效率的定义如公式(12)所示。引入欧洲效率的概念后，要充分考虑不同负载下逆变器各部分的损耗。由公式(12)可得光伏逆变器欧洲效率表达式如公式(13)所示。

其中，wi表示权重，Pli表示电抗器总损耗，Potheri表示逆变器除电抗器外的损耗，P0表示满载时逆变器的总功率，ratingi表示不同的负载比例。从公式(13)可以看出，逆变器的欧洲效率与不同负载下逆变器的总损耗相关，因此，为了获得最高的欧洲效率，除了要均衡电抗器损耗与逆变器其他损耗的比例外，还必须均衡各个负载下逆变器总损耗的比例。由上文的分析可知，忽略气隙扩散磁通的影响后，电抗器的总损耗是绕组损耗与铁芯损耗之和。绕组损耗与铝箔的匝数和厚度相关，铁芯损耗与铝箔的匝数相关，因此，存在一个最优的铝箔厚度和匝数使逆变器的欧洲效率最大。图9所示为在考虑逆变器其他损耗的情况下，电抗器取不同匝数时，铝箔厚度与欧洲效率的关系曲线。其中，横坐标表示铝箔厚度(单位:0.1mm)。从图中可以看出，每一个铝箔匝数都会各自对应使欧洲效率最高的铝箔厚度，且存在一个最优的铝箔匝数使逆变器的欧洲效率最高。当铝箔匝数取16匝，铝箔厚度取1mm时，逆变器的欧洲效率最高，可以据此优化电抗器的参数。

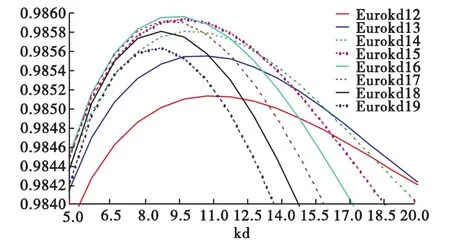
图9 欧洲效率与铝箔匝数和厚度关系

5 结论

本文基于欧洲效率对一个容量为500kVA的三相光伏逆变器的电抗器进行详细的损耗分析，并得出以下结论:

(1)铁芯采用多段分布气隙的方式以减小气隙扩散磁通产生的附加损耗，当忽略气隙扩散磁通的影响时，电抗器的绕组损耗模型可以近似等效为一维涡流理论模型。

(2)忽略气隙扩散磁通产生的附加损耗，电抗器的总损耗可以表示为绕组损耗与铁芯损耗之和。绕组损耗与铝箔的匝数和厚度相关，铁芯损耗与铝箔的匝数相关，因此存在一个最优的铝箔厚度和匝数使电抗器的总损耗最小。

(3)由于光伏逆变器负载变化的特殊性，本文考虑不同负载情况对电抗器的损耗进行分析可知，电抗器的总损耗随着负载的增加而增加，每一个负载都会对应各自的使电抗器总损耗最小的铝箔匝数和厚度。

(4)考虑逆变器各部分的损耗可以得到一个最优的欧洲效率，在该点会对应最优的铝箔厚度和匝数，以此优化电抗器的参数。

［1］李翔，马超群，梁琪，等.大功率光伏逆变器耗建模分析［J］.电力电子技术，2014，48(1):12－14.

［2］任玉艳，高金玲，郑存芳，等.三相光伏并网逆变器开关损耗抑制策略［J］.电力电子技术，2014，48(3):7－9.

［3］G.Bertotti.General properties of power losses in soft ferromagnetic materials.IEEE Transactions on Magnetics，1988:621－630.

［4］Colin J.Dunlop.Modeling Magnetic Core Loss for Sinusoidal Waveforms.B.S.，Electrical Engineering United States Naval Academy，2002.

［5］Reinert，J，Brockmeyer，A，De Doncker，R.W.A.A.Calculation of losses in ferro-and ferromagnetic materials based on the modified steinmetz equation.IEEE Transactions on industry applications，37(4)，2001:1055－1061.

［6］旷建军，郑力新，卢小芬，等.非正弦励磁下铁芯损耗的计算［J］.磁性材料及器件，2009:44－46.

［7］Rudy Severns.HF core loss for non－ sinsoidal waveforms.Proc.HFPC'91，1991:140－148.

［8］P.L.Dowell，B.Sc.(Eng.).Effects of eddy currents in transformer windings［J］.IEEE Trans on Power Systems，1996，113(8):1387－1394.

［9］Hu J，Sullivan C R.The quasi-distributed gap technique for planar inductors:design guidelines.IEEE IAS，New Orleans，USA，1997:1147－1152.

［10］旷建军，阮新波，任小永，等.气隙设计对电感绕组损耗的影响［J］.电子元件与材料，2007，26(10):60－63.