灰色理论在基线解算中的应用研究

吝志勇，蓝悦明

(1.保定市城市设计院，河北 保定071000;2.武汉大学 测绘学院，湖北 武汉430079)

如何在尽可能短的时间内，获得尽可能高精度的结果，是GNSS 应用研究领域的热点问题。目前的研究多是基于大样本数据考虑的，对小样本数据的情况考虑较少，而灰色系统理论的特色就是研究“小样本”、“贫信息”的不确定性问题。灰色系统理论认为，尽管客观系统的表象复杂，数据凌乱，但它们总有自身的整体功能，必然蕴藏某种内在规律，关键是如何选择适当的方法去挖掘和利用它［1］。

1 灰色理论序列算子构造与数据重生成

1.1 序列算子

对于GNSS 测量而言，由于观测过程中受到诸如与卫星有关的误差、信号传播误差、与接收机有关的误差，以及其他误差等的影响，相应的观测值序列是一个冲击扰动序列，要从冲击扰动序列出发实现对真实行为序列系统变化规律的正确把握和认识，必须首先设法排除系统行为数据所受到的冲击波干扰，还数据以本来面目。设：

式(1)为系统真实行为序列，而观测到的系统行为数据序列为：

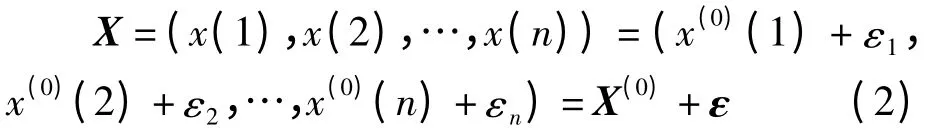
式中：ε=(ε1，ε2，…，εn)为冲击扰动项，X为冲击扰动序列。

设D为作用于X的算子，X经算子D作用后所得序列记为：

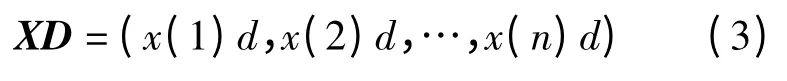
其中，XD为一阶算子作用序列。

序列算子的作用可以进行多次，相应地，有二阶、三阶算子作用序列。

1.2 实用缓冲算子的构造

设原始观测值序列为：

则当X为单调增长序列、单调衰减序列或震荡序列时，D皆为弱化算子。

2 方程病态性及其改善

2.1 方程病态性讨论

利用少数几个历元的观测数据进行基线解算时，由误差方程组成的法方程是一个病态方程［2-3］。由于法矩阵条件数较大，法矩阵求逆不稳定，观测值微小的变化会导致解不稳定。

Gauss-Markov 模型为：

式中：A为系数矩阵;X为待求参数向量;L为观测值;Δ 是观测噪声;P为相应观测值的权阵。相应参数X的最小二乘解为：

其中：N=ATPA;W=ATPL。当法矩阵非奇异时，参数解存在且唯一;假设N、W有微小的扰动δN、δW，引起估计量有偏差δ，可表示为：

显然，δN、δW对δ的影响与N-1密切相关。如果N的条件数比较大，当N、W有一个微小的变化时，参数解相应将产生较大的变化。

2.2 方程病态性改善

有偏估计中的岭估计是克服方程病态性的常用方法，而岭参数的选择又是其中的关键和难点。根据TIKHONOV 正规化原理，对应式(5)岭估计的估计准则为：

相应岭估计的解为：

考虑到少数几个历元数据组成的法矩阵特征值较大，选取正规化矩阵R代替式(9)中的单位矩阵I，相应的方法称为修正的TIKHONOV 正规化方法，估计准则为：)

经大量实际算例研究证明，用L 曲线法选取正规化参数α =1 时效果最好，正规化矩阵R的选取方式有很多［4-7］，笔者采用如下的形式：

式中：j为组成法方程的历元数;I为3 ×3 的单位矩阵;β 为权比系数，可以根据待定点近似坐标的偏差和相位观测值的精度比来确定，经多个实例验证，其取值范围为10-6～10-4。于是，正规化后的参数解为：

与最小二乘中的法矩阵相比，式(12)中的法矩阵中增加了R项。该措施的实质是在基线分量对应的部分附加微小的约束，并让正规化矩阵随着历元数的变化而变化，正是由于R的参与，法矩阵的病态性得到抑制。

3 实例分析

灰色理论缓冲算子的引入可以减弱观测数据中某些不确定性误差的影响，改善观测值的质量。从定性分析的角度来看，利用缓冲处理后的数据进行参数解算应能取得较好的结果。为了体现小样本数据的特点，实验中均选取了5 个历元的观测值。观测值选取时，尽量选在卫星观测信号连续且稳定的时间段内，以避免粗差或周跳等带来的影响。实验中，首先利用软件TGO 对整个时段(1.5 h)内的观测值进行平差计算，作为待求基线解的真值。实验中笔者设计了3 种不同的方案：

(1)利用原始观测数据组成同步观测值，建立单差、双差模型，在双差模式下求解模糊度浮动解，再根据模糊度浮动解及方差协方差阵，进行模糊度搜索与固定，最终求得基线参数的固定解。

(2)利用原始观测值φi进行序列算子构造并对原始观测值序列φ 进行缓冲处理，得到新的观测值序列φ'(虚拟观测值序列)后再建立双差模型进行参数求解计算，参数解算同实验方案(1)。

(3)利用两个不同测站的原始观测值φi、φj，组成双差观测值φ▽Δ，然后用双差观测值来构造缓冲序列算子，进行双差观测值序列的重生成，最后用新生成的双差观测值φ'▽Δ进行参数的求解计算。3 种实验方案解算过程如图1 所示。

图1 基线解算处理流程图

为了验证上述3 种方案的解算效果，笔者选取了3 条不同长度的基线观测数据进行解算，解算结果如表1 所示。

表1 基线解算结果对比表

从表1 可以看出：对于第一条基线来说，方案(2)、方案(3)的解算效果要优于方案(1)，利用缓冲后的数据求得的结果更接近真值;对于后两条基线来说，方案(2)的效果最好，解算的结果更接近真值。

4 结论

对于给定不同长度的基线观测数据，尤其是短基线观测数据来说，利用灰色理论缓冲算子对少数几个历元的观测数据进行数据重生成，然后再进行参数求解计算，其结果比数据直接解算的效果要好，说明灰色理论在短基线解算中具有一定的优越性。

［1］ 邓聚龙.灰色理论基础［M］.武汉：华中科技大学出版社，2002：153 -192.

［2］ 郭建峰. 测量平差系统病态性的诊断与处理［D］.郑州：中国人民解放军信息工程大学，2002.

［3］ 林胜良.病态线性方程组解法研究［D］.杭州：浙江大学，2005.

［4］ 崔希璋，於宗俦，陶本藻，等.广义测量平差［M］.武汉：武汉测绘科技大学出版社，2001：163 -170.

［5］ 王振杰.大地测量中不适定问题的正规化解法研究［D］. 武汉：中国科学院测量与地球物理研究所，2003.

［6］ 阳仁贵，欧吉坤.提高GPS 单频相位模糊度解算成功率的新方法［J］. 南京航空航天大学学报，2005，37(3)：279 -283.

［7］ 王振杰，欧吉坤，田爱奎.改进的ARCE 方法及其在单频GPS 快速定位中的应用［J］. 武汉大学学报(信息科学版)，2005，30(6)：488 -491.