基于递归秘密共享的可靠云存储方案

王家玲

一、引言

云存储是云计算技术[1]的一个延伸，可以认为它是一个配备了海量存储空间的云计算系统。但是，由于云存储系统规模巨大，集中了诸多用户的应用和隐私数据，同时云存储具有前所未有的开放性和复杂性，其安全性面临着比传统信息存储更为严峻的挑战[2]。因此，设计安全可信的云存储方案具有重要的实践意义。

本方案利用递归的门限秘密共享方案，实现数据资源的拆分和冗余存储。方案不仅能有效保证云存储数据的机密性，还能实现数据的冗余存储，且方案的存储开销较传统的完全冗余存储以及基于Shamir(k,n)秘密共享存储存储降低了很多，大大节约了存储空间。

二、相关工作

云存储的安全问题主要集中在数据的机密性和完整性。就机密性而言，加密技术是保护数据机密性的一种较为有效的手段。在数据被存储到云端之前，我们可以对数据进行加密，这样云服务商和攻击者都无法获得数据的明文内容。用户可以通过密文检索技术来访问数据。但是这种方法多用于静态数据云存储的场景，不适合数字资源不断动态更新的场景。

就完整性而言，对于用户来说，由于不存储数据的备份，因此，能够确保数据在云端服务器上的完整性至关重要。数据冗余存储是目前来说比较有效的手段。目前，主要的冗余方法有两种：完全副本冗余和纠错码冗余。完全副本冗余是指保存多份数据的完整副本，只要还有一个副本可以访问，数据就不会丢失。侯孟书等[3]为被频繁访问的数据增加副本数量，并选择高性能存储节点存放，从而提高数据的可用性。完全副本冗余虽然简单、直观，但是有存储空间消耗大，处理大文件时性能差等缺点。

纠错码是指将存储的数据先切分为m个部分，然后编码变换成n(n>m)个部分，恢复数据时只要得到其中任意t(t≥m)个部分即可。目前，大多数云存储模型中使用纠删码算法将数据分割来提高数据的冗余性。Weatherspoon等[4]采用随机过程的方法，量化分析了完全副本冗余和纠错码对系统可靠性的影响，发现使用纠错码冗余，可以在与副本冗余得到相同可靠性的条件下，极大地节约系统中的存储空间和维护带宽。不过该算法得到的数据都是以明文形式显示的，因此数据的机密性无法保证。

为保证数据的机密性和冗余性，一些云存储模型使用门限秘密共享算法实现云存储。(k,n)门限秘密共享方案是把一个数据分成n个秘密份额分给n个参与者掌管，这些参与者中k个或k个以上的参与者所构成的子集可以合作重构这个秘密。研究者们利用多种数学模型构建了多种门限秘密共享方案[5]～[9]，这些方案不仅能保证数据的冗余存储，还能提供机密性的保证。但是该算法会带来存储空间的剧增，造成用户成本的增加。

为此，本文提出一个既能保证数据冗余存储又能提供数据机密性的可靠云存储方案，该方案采用基于递归的秘密共享算法将数据进行分割，分割后每个数据块的大小比源数据小很多，不会带来存储空间的剧增。方案的安全性由需存储的数据块的大小决定，数据越大，安全性越高，故适合海量数据的云存储情况。

三、可靠冗余存储方案

方案的基本思想是基于递归的(k,n)门限秘密共享方案[10]，将数字资源S分割转换成n个数据块，分别保存在云存储系统的多个服务器上，至少k个完整数据分块组合可以恢复原来的数据，任意k-1个或更少完整数据块不能重构S，且不能获得有关S的任何信息。数据块完整性的判断，通过数据完整性检测算法实现。这不但实现了数据的冗余存储，只要服务器上至少有k个数据块没被损坏，就能恢复出原来的数据；又保证了数据的机密性，攻击者只有攻破至少k个数据块才能恢复数据S，否则不能获得有关S的任何信息。

1.方案框架

数字资源云存储过程如下：若数字资源S能平均分块，则将S平均分割成k个大小相同的数据块S1,S2,…,Sk；若S长度不能被平均分块，则先将S分成长度为的k-1个数据块，最后一个长度小于的数据块，可通过数据前方补零的方法使其与前面k-1个数据块长度相等，故通过数据前方补零的方法可使S平均分割。因此，为了不再赘述，可假设文后的数字资源长度均能被平均分块。数字资源持有者随机选择一个数据a，与S1,S2,…,Sk一起作为RSS分发算法（递归秘密共享算法的分发阶段）的输入，通过该算法转换输出n个数据大小相同的数据块D1,D2,…,Dn，然后再将各数据块划分成m个数据块并生成其签名，将数据分别发送存储到云端的多个服务器上，用户随时通过数据完整性检测算法检测云服务器上数据的完整性，若想恢复数据S，只需在云存储服务器上下载任意k个无损坏的数据块，利用RSS重构算法（递归秘密共享算法数据重构阶段），即可获得S1,S2,…,Sk，从而得到原始数据S。方案框架如图1所示。

图1 方案框架图

2.具体方案描述

本方案假设云存储商是半可信的，即云服务商不会主动泄露和破坏用户存储的数据，但是不能完全保证因为机器故障或黑客攻击导致数据的泄露与破坏。本方案是递归的采用Shamir的(k,n)门限秘密共享算法，对各数据块进行自加密以保证数据的机密性和冗余存储。

令p是大素数，满足p>max(Smax,n)，其中Smax=max(Si)（1≤i≤（k-1））。数字资源记为S，被平均划分成大小相等的k个数据块记为|S1|=|S2|=…=|Sk|，k为门限值。递归的Shamir的 (k,n)门限秘密分发算法记为RSSDeeling(S,a)，其中S为原始数据，a为预先生成的一个随机数据，a ZP，n为最终转换的数据块的个数。D1,D2,…,Dn为转换后的数据块，即函数RSSDeeling(S,a)的输出。再将每个数据块分成m个小数据块，第i个数据块记为Dij（1≤j≤m），它的数字签名记为RSSProof(i,Vij)算法为数据块Dj的完整性检测算法，其中Vij（VijZP）是为数据块Dij选取的随机数。RSSRecover(N1,N2,…,Nk)为数据重构算法，其中N1,N2,…,Nk是从云存储设备上下载的任意k个完整数据块。

整个方案分为三个过程：分发存储过程、完整性检测过程和数据重构过程。

(1)分发存储过程

a.将数字资源S切割成大小相等的k个数据块，记为|S1|=|S2|=…=|Sk|，S={S1,S2,…,Sk}；

b.选择数据a ZP，构造一次多项式f1(x)=ax+S1；

d.当 2≤i≤（k-1）时，构建如下多项式：

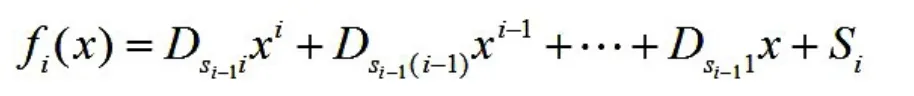
I.当 i＜（k-1）时，计算 i+1 个点：

II.当 i＝k-1 时，计算 n 个点：

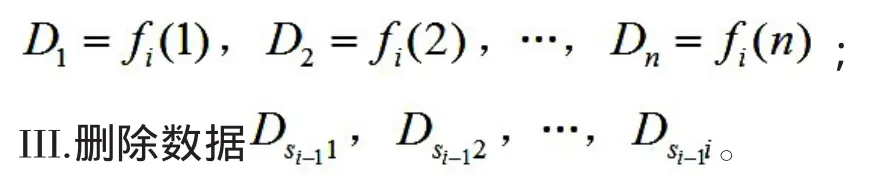
e.将各数据块再平均划分成m个小数据块，利用数字签名算法，生成各数据块Dij（1≤i≤n,1≤j≤m）的签名，其中，H是hash函数，可将任意长度的二进制字符串映射为群G上的元素；μ是群G的生成元；α是用户私钥，V=gα是公钥。

(2)完整性检测过程

用户将数据发送至云存储器后，可通过可恢复性完整性验证算法RSSProof(j,Vij)[11][12]来检测云存储服务器上的数据的完整性，这里以其中的一个数据块Di为例，其他数据块方法类似，不再赘述。

a.为小数据块Dij生成一个挑战对(j,Vij)，构成挑战集合

b.针对挑战对，云存储服务方首先将其对应数据块平均划分成m个小数据块Dij，给出应答对 ，其中。

c.用户通过判断方程 是否成立来判断第i个数据块Di是否完整，该方程中的e是密码学中的双线性映射方程。

下面证明一下完整性检测判断方程能否判断数据的完整性。

由双线性映射的重要性质可知，

等式左边：

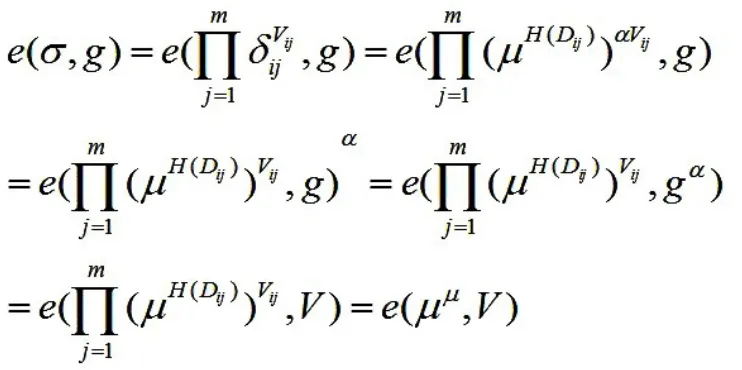
因此，若数据完整没发生任何变化，等式成立；反之，若数据发生变化，则等式不成立。

(3)数据重构过程

用户根据完整性检测结果来选择是否要进行数据重构。如果服务器上的n个数据块中，有大量数据块被损坏，但是被损坏的数据块个数不多于n-k个，那么完整的数据块不少于k个，这时，我们可以选择使用数据重构算法来重构数据S。如果损坏的数据块个数超过了n-k个，则无法重构数据。数据重构过程如下：

a.从云存储服务器上下载k个完整的数据块（i,Di）1≤i≤k；

b.使用拉格朗日插值公式构造多项式：

计算Sk-1=fk-1（0）.

c.当 2≤i≤（k－1）时，

计算Si=fi（0）.

四、方案分析

1.机密性

由于数据在存储到云端服务器之前，我们将数据进行了分割和转换，转换后的数据与原数据截然不同。用户数据文件变换后内容与原文件相比发生了变化，对于外部攻击者来说，获得某个分块并不能知晓有关原文件的任何内容，黑客如想得到原数据的有关信息，必须要同时攻破多个服务器，至少获得k个数据块信息，才能通过恢复算法获得原数据S。若攻击者获得少于k个数据块的信息，将得不到有关S的任何信息。不是一般性，假设攻击者获得k-1个数据块信息，相当于已知一个k次多项式的k-1个点，无法唯一确定该多项式。相当于在Zp内随机猜测数据S，其概论为1/p。而攻击者同时攻破多个服务器，且获得k个相关数据块的概率很小，显然加大了攻击者攻击的难度。这就有效的保证了数据在存储到云存储服务器上的机密性。数据块越大，素数p要求越大，这样猜测S的概率越小，数据安全性越高。

2.冗余性

由于该方案是一个(k,n)门限秘密共享方案，即我们将原始数据S经过转换后，生成了n个分块，而其中任意k个分块组合，通过数据恢复算法可恢复出原数据S。如果服务器上的n个数据块中，有大量数据块被损坏，但是被损坏的数据块个数不多于n-k个，即完整的数据块不少于k个，这时，我们可以使用数据重构算法来重构数据S。即该方案允许损坏的数据块的个数最多为n-k个。如果损坏的数据块个数超过了n-k个，则无法重构数据。

3.存储开销

服务器端的存储开销主要由冗余机制引入，由秘密共享方案的冗余度决定。对一个数据S，令|S|表示秘密的大小，若使用经典的Shamir(k,n)秘密共享方案，产生的每个数据块大小为均|S|，若产生n个数据分块，云存储服务器上需存储的数据大小将为n×|S|，空间效率较低。原数据S越大，空间效率将越低，不适合海量信息的存储。在本方案中，采用的是基于递归的Shamir(k,n)秘密共享方案，首先将秘密S分为大小为的k个数据分块，若转换成n个数据分块，则云存储服务器上需存储的数据大小将为大大节约了存储空间，有很高的空间效率。故本方案中的冗余存储机制尽可能地降低了云存储服务器的存储开销。

五、结束语

随着云存储的出现，海量的数字资源存储到云端服务器成为必然趋势。但是云存储的安全问题面临着越来越严峻的挑战。为保证数据的保密性和冗余性，本文提出了一个高效可靠的云存储方案，方案由三部分组成，即：数据分块分发过程、数据完整性检测过程和数据重构过程。文章通过分析方案的机密性、冗余性和存储开销得出所提方案的优越性。

[1]HayesB.CloudComputing[J].Communications of the ACM,2008,51(7):9－11.

[2]冯登国,张敏,张妍，等.云计算安全研究[J].软件学报，2011，22(1):71-83.

[3]侯孟书,王晓斌,卢显良，等.一种新的动态副本管理机制[J].计算机科学,2006,33(9):50-51.

[4]Weatherspoon H,Kubiatowicz J.Erasure coding vs replication:quantitative comparison[M].In:Proc of the 1st Int'l Workshop Peer-to-Peer Systems,2002.

[5]Shamir A.How to Share a Secret[J].Communications of the ACM，1979，22(11):612-613.

[6]Blakley G.Safeguarding Cryptographic Keys[C].Proceedings of the National Computer Conference,Montvale:NCC,1979:242-268.

[7]Asmuth C.,Bloom J.A Modular Approach to Key Safeguarding[J].IEEE Transactionson Information Theory,1983,29(2):208-2I0.

[8]Karnin E.D.,Green J.W.,Hellman M.E..On Sharing Secret Systems[C].IEEE Transactions on Information Theory,1983,29(1):35-41.

[9]Feldman P.A Practical Scheme for Non-interactive Verifiable Secret Sharing[C].Proceeding of 28th IEEE symposium on Foundations of computer science,Canada:IEEE,1987.427-437.

[10]Parakh A,Kak S.Space efficient secret sharing for implicit data security[J].InformationSciences,2011,181(2):335-341.

[11]D.L.G.Filho,P.S.L.M.Barreto.Demonstrating data possession and uncheatable data transfer[R/OL].Cryptology ePrint Archive,Report 2006/150,2006.

[12]Y.Deswarte,J.-J.Quisquater.Remote Integrity Checking[C].Sixth Working Conference on Integrity and Internal Control in Information Systems.Kluwer Academic Publishers,2004.1－11.