简谐势+四次势阱中两组分自旋轨道耦合旋转玻色爱因斯坦凝聚体
陈光平
(四川文理学院物理与机电工程学院,四川达州635000)
简谐势+四次势阱中两组分自旋轨道耦合旋转玻色爱因斯坦凝聚体
陈光平
(四川文理学院物理与机电工程学院,四川达州635000)
采用中心差分和虚时演化数值实验方法研究了简谐势+四次势阱中自旋轨道耦合作用下的两分量旋转玻色爱因斯坦凝聚体。发现自旋轨道作用强度和原子种间相互作用对系统基态结构有着重要的影响,原子种间相互作用强度的增加可使系统从相混合变化成相分离;而自旋轨道耦合作用强度的增加,可使系统从相分离的状态变化成相混合,并产生涡旋、形成分块边界。
自旋轨道耦合;玻色-爱因斯坦凝聚;两分量;简谐势+四次势;基态
最近,人工合成非规范阿贝尔势在理论和实验上取得了巨大成功,人们开始研究利用非规范阿贝尔势来实现中性原子自旋轨道耦合以研究超冷原子构成的玻色爱因斯坦凝聚体的性质,经过多年研究,在理论上和实验上均取得了丰富的成果[1-4]。然而,已有研究基本上是囚禁于简谐势阱中的自旋轨道耦合作用下的玻色爱因斯坦凝聚体,也有研究者研究了囚禁于共心双环势阱中的自旋轨道耦合作用下的玻色爱因斯坦凝聚体[5-8]。以上两种势阱中的玻色爱因斯坦凝聚体的旋转角频率不能大于简谐势和共心双环势阱的约束频率,如果超过约束频率,系统将因受到强大的离心力作用而散落。为了解决这一难题,文献[9][10]中作者Alexander L.Fetter构造了简谐势+四次势阱,囚禁于其中的单组分玻色爱因斯坦凝聚体可以抵挡强大的旋转离心力而不至于散落。在文献[11]中研究了简谐势+四次势阱中两组分旋转玻色爱因斯坦凝聚体的性质,发现它们的基态结构随着种间原子之间相互作用强度和旋转角频率的关系,文章将引入自旋轨道耦合,进一步研究简谐势+四次势阱中两组分旋转玻色爱因斯坦凝聚体的性质;因为自旋轨道耦合的引入,加大了系统可调控参数空间,所以系统必将产生更多新奇的量子效应,本研究的目的主要是去发现这些新奇的量子效应。
1 理论模型
文章主要研究两分量自旋轨道耦合作用旋转玻色爱因斯坦凝聚体,系统哈密顿量为:
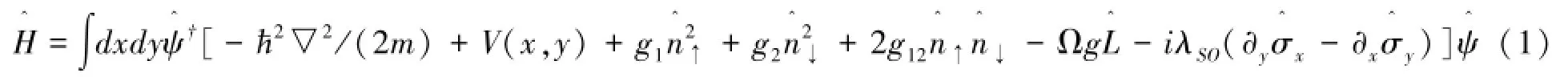
势阱函数描述为:

势中d⊥=ћ/mω⊥是谐振子长度,ω⊥是准二维平面谐振子的约束频率,r是径向坐标,λ为四次势阱强度的无量纲常数。
根据平均场近似,推知Gross-Pitaevskii能量函数为

其中c0=g+g12,c2=g-g12.设旋转轴为z轴Ω=Ωz^,旋转部分可以写为

文章采用虚时演化和中心差分相结合的方法来求解具有自旋轨道耦合相互作用的旋转凝聚体的基态结构。为了计算方便,定义单位长度d0=[ћ/mωω⊥]1/2,相互作用单位能量ћω⊥。
2 结果与分析
在本研究中,由于自旋轨道耦合的引入,大大拓宽了系统的可调控参数空间,将固定同种原子之间的相互作用强度为g=g1=g2=500和旋转角频率Ω=0.5,只研究原子种间相互作用强度g12和自旋轨道耦合强度λSO的变化对系统基态结构的影响。本研究数值实验选取的单位长度为图1展示出系统基态密度分布与原子种间相互作用强度和自旋轨道耦合强度的变化关系。
从图1第一列第一排和第二排可以看出,因为没有自旋轨道耦合的影响,当原子种间相互作用强度g12小于原子种内相互作用强度g时,赝自旋向上和赝自旋向下的两种原子基态处于相混和状态。当原子种间相互作用强度g12大于原子种内相互作用强度g时(见第一列第三排第四排),两种原子开始呈现相分离状态;对比第一列图(a)和图(b)还可以发现,原子种内相互作用强度为零时,尽管旋转角频率Ω=0.5,但是两种原子基态依然是圆盘状平面波结构,而增大原子种间相互作用g12=400时,在赝自旋向上和赝自旋向下两种原子的基态中,都出现了一个涡旋,由此可见,原子种间相互作用对系统基态结构中产生涡旋有较为重要的影响作用。
图1(a)所示,系统在无原子种间相互作用时,随着自旋轨道耦合的加入并增加,两种原子的基态结构分布对称性逐渐发生破缺,在自旋向上和自旋向下两种原子基态结构中出现了涡旋,虽着自旋轨道耦合强度λSO增加,涡旋的数目逐渐增加;当λSO增加到3时,这些涡旋的密集分布恰好将圆盘状的平面波分布分成四块,涡旋就成了分界线(有文献中称它为“Domain”)。在图1(b)中,因为原子种间强度增加到g12=400,即使没有自旋轨道耦合,在第一列基态分布图中也出现了少量的涡旋,自旋轨道耦合强度λSO增加时,涡旋数目也逐渐增加,对比图1(b)和图1(a),可以看出,原子种间相互作用强度在小于原子种内相互作用强度情况下,对产生涡旋的数目有重要的影响作用;在这两排图中,还可以得知,自旋轨道耦合强度对产生涡旋的数目也有重要的影响作用。
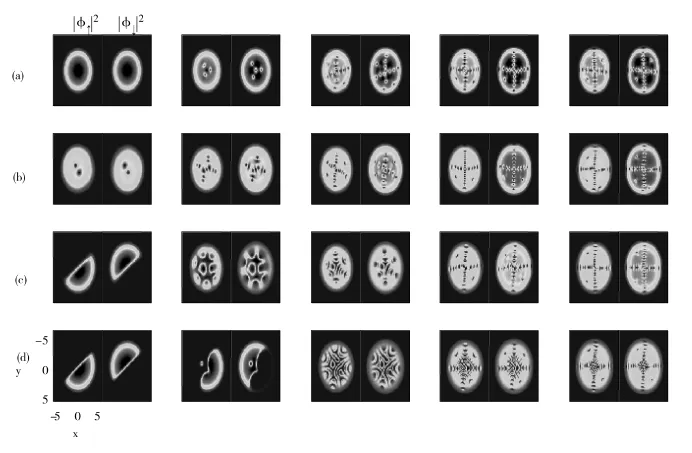
图1 两组分自旋轨道耦合作用下旋转凝聚体的基态结构相图
在图1(c)和图1(d)中,发现当g>g12时,无自旋轨道耦合作用下,系统自旋向上和自旋向下两种原子基态处于相分离状态,当系统引入自旋轨道耦合并增大时,系统基态逐渐从相分离走向相混合;进一步增加自旋轨道耦合强度到λSO=5时,惊奇发现在已经处于相混合的两种原子基态中,出现了涡旋,且涡旋的排列恰好也形成了边界(Domain),它们也将系统的基态分成四块区域。对于这一现象的解释是因为在简谐势+四次势阱中,可以对凝聚体施以很强的自旋轨道耦合,所以才会使原来处于相分离的凝聚体转化为相混合,而进一步加大自旋轨道耦合后,在相混合基态中就会出现涡旋组成的边界(Domain)。
3 结论
文章主要研究了囚禁于简谐势+四次势阱中两组分自旋轨道耦合作用下玻色爱因斯坦凝聚体的基态结构。研究发现,在简谐势+四次势阱作用下,种间原子相互作用对系统的基态结构有重要的影响,可以使系统从相混合走向相分离,并且对涡旋结构的产生有着重要的影响作用;自旋轨道耦合的引入并加强,可以在系统原来是相混合的基态结构中产生涡旋并形成边界(Domain),也可以使原来处于相分离的基态结构走向相混合,并且产生涡旋、形成边界(Domain)。总之,自旋轨道耦合的引入,使系统的基态结构得到了极大的丰富,产生了新奇的量子效应。这为在实验上实现两组分自旋轨道耦合作用旋转玻色爱因斯坦凝聚和认知它的宏观量子效应有着重要的指导意义。
参考文献:
[1]M.R.Matthews,B.P.Anderson,P.C.Haljan,et al.Vortices in a Bose-Einstein Condensate[J].Phys.Rev.Lett.1999,(83):2498-2504.
[2]K.W.Madison,F.Chevy,W.Wohlleben,and J.Dalibard.Vortex Formation in a Stirred Bose-Einstein Condensate[J].Phys.Rev.Lett,2000,(84):806-811.
[3]J.R.Abo-Shaeer,C.Raman,J.M.Vogels,and W.Ketterle.Observation of Vortex Lattices in Bose-Einstein Condensates[J].Science,2001,(292):476-480.
[4]C.Raman,J.R.Abo-Shaeer,J.M.Vogels,K.Xu,and W.Ketterle.Vortex Nucleation in a Stirred Bose-Einstein Condensate[J].Phys.Rev. Lett,2001,(87):210402-210408.
[5]P.C.Haljan,I.Coddington,P.Engels,and E.A.Cornell.Driving Bose-Einstein-Condensate Vorticity with a Rotating Normal Cloud[J].Phys. Rev.Lett,2001,(87):210403-210409.
[6]ZHANG Xiao-Fei,DONG Rui-Fang,LIU Tao,et al.Spin-orbit-coupled Bose-Einstein condensates confined in concentrically coupled annular traps[J].Phys.Rev.A,2012,(86):063628.
[7]ZHANG Xiao-Fei,GAO Ri-Sheng,WANG Xin,et al.Bose-Einstein condensates in concentrically coupled annular traps with spin-sorbit coupling and rotation[J].Physics Letters A,2013,(377):1109-1113.
[8]ZHANG Xiao-Fei,LI Biao,ZHANG Shou-Gang.Rotating spin-orbit coupled Bose-Einstein condensates in concentrically coupled annular traps[J].LASER PHYSICS,2013,(23):105501.
[9]Alexander L.Fetter,B.Jackson,and S.Stringari.Rapid rotation of a Bose-Einstein condensate in a harmonic plus quartic trap[J].Phys.Rev.A,2005,(71):013605.
[10]A.L.Fetter,Rotating vortex lattice in a Bose-Einstein condensate trapped in combined quadratic and quartic radial potentials[J].Phys.Rev.A,2001,(64):063608-063617.
[11]陈光平.囚禁于简谐势+四次势阱中两分量玻色爱因斯坦凝聚体的研究[J].四川文理学院学报,2014,(5).
Two-component Bose-Einstein Condensates in Harmonic Plus Quartic Potential with Spin-orbit-coupled and Rotation
CHEN Guang-ping
(School of Physics and Mech-tronic Engineering,Sichuan University of Art and Science,Dazhou,Sichuan,635000,China)
The two-component Bose-Einstein condensates in harmonic plus quartic potential with spin-orbitcoupled and rotation have been studied by the finite difference and image-time propagating numerical method.It is found that the inter-component interaction and the strength of the spin-orbit-coupled play an important role in the system's ground states.The system can transform from the phase co-exist to the phase separation with the increase of the inter-component interaction;with the increase of the strength of spin-orbit-coupled,the system can trans⁃form from phase separation to phase co-exist,at the same time,there are vortex and domain in the ground state of the system.
Spin-orbit-coupled;Bose-Einstein condensates;Two-component;Harmonic plus quartic po⁃tential;Ground state
O562
A
1008⁃9659(2015)01⁃0001⁃04
2015-01-10
四川省科技厅资助项目(2011JY0063);四川省教育厅资助项目(2ZA148,12ZB313,12ZZ021)。
陈光平(1981-),男,四川大英人,讲师,博士研究生,主要从事冷原子方面研究。

