基于压缩感知理论的时变信号压缩技术
郭 亮, 高宏力, 黄海凤, 张筱辰
(西南交通大学机械工程学院,四川成都 610031)
近年来,随着计算机技术的发展和企业设备管理要求的提高,大型机械设备的在线监测与诊断系统正朝着网络化和远程化的方向发展.但是工业现场采集信号数据量大,且有一定的冗余度,这给网络实时传输带来一定挑战.另外由于现场工况复杂和传感系统自身的原因,采集信号含有噪声.所以在传输过程中需对信号进行压缩和去噪处理,无论对减少传输时所用带宽还是提高信号的信噪比都具有重要意义[1].
大部分的机械振动信号都是时变信号,目前,常用的时变信号压缩方法主要有无损编码的算术编码、霍夫曼编码和有损编码的数据稀疏化、正交变换、预测编码[1-2]等,其中,基于小波变换的数据稀疏化压缩方法是目前较通用的方法,也是效果较好的一种方法[3].小波变换能较好地刻画信号的时频局部特征,适用于机械振动时变信号的压缩和编码.由于信号的压缩与去噪效果与小波基的选择有很大的关系,因此基于小波变换的信号压缩和去噪需要有处理信号的先验知识,自适应能力不强.
压缩感知是继小波分析和多尺度集合分析之后,于2006年由Candes等[4-7]提出的一种新的信号分析理论.其基本思想是:若信号是稀疏的或者是可压缩的(或者是在某个变换域内满足这两个条件),那么信号可以由测量矩阵将原始信号变换为低维信号,再通过重构算法优化求解得到原始信号.在该理论框架下,信号采样和压缩不取决于信号带宽,而取决于信号本身的结构和内容.压缩感知理论与传统的内奎斯特采样定义不同,它提出了将模拟信号直接采样压缩为数字形式的有效途径,给信号采样方法带来了一次新的革命[8],其在图像压缩、图像识别和图像去噪[9-11]领域取得了突破性的进展.但是,目前应用压缩感知理论进行机械振动信号处理的研究还鲜见报道[12-13].
针对上述问题,本文提出了一种基于压缩感知的时变信号压缩算法(time-varyingsignal compressed algorithm based on compressed sensing,TvCS).该算法以压缩感知理论为基础,应用有限等距性质作为限制条件构造稀疏矩阵和测量矩阵,在稀疏矩阵上构建压缩信号,再通过正交匹配追踪算法重构出原始信号.理论分析和实验都证明了该算法的有效性和实用性.
1 压缩感知理论
在传统的内奎斯特(Nyquist)采样模式下,
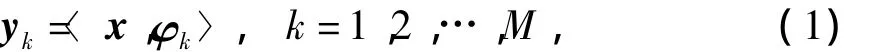
式中:x∈RN为原始信号;yk为采样点;φk为采样向量(函数),采样过程需要满足fs≥2f,其中fs为采样频率,f为原始信号频率.
若取M≪N,即当原始信号x∈RN在具有一定稀疏性的情况下,测量值的大小远小于原始信号小大,这个过程称为压缩感知:

式中:x∈RN为 k-稀疏原始高维信号;y∈RN为M 维的低维压缩测量向量;Φ =[φ1,φ2,…,φM]为M×N阶测量矩阵,或称为抽样矩阵.
但在现实中,信号x∈RN并不都具有稀疏性,需要构造稀疏矩阵,使信号在稀疏矩阵ψ空间内可以稀疏表示.假设{ψi}∈RN是一组基向量,则任何信号x∈RN都可以线性表示为

式中:s是 x在 ψ 域的变换向量,si=〈 x,ψi〉=x,ψ=[ψ ,ψ ,…,ψ ]是 N × N 阶变换矩阵.12N如果式(3)的线性表示只需不大于K的基向量{ψi}i∈Ω,Ω∈{1,2,…,N},|Ω| ≤K,可以说变换向量s中最多有K个非零项{si≠0}i∈Ω.
因此,压缩感知的过程变为

式中:Φ为测量矩阵;ψ为稀疏矩阵;s为原始信号;y为压缩采集信号;θ为测度矩阵.
压缩感知的信号重构是研究从测量值y∈RN中恢复出x.该问题在数学上是一个求l0范数最小化问题:
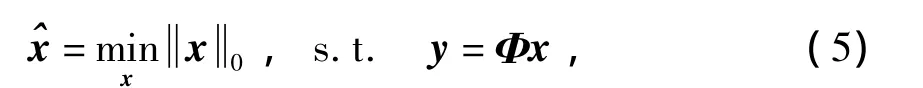
l0范数最小化的问题是一个NP难问题,通常用贪婪方法求解,主要包括匹配追踪(MP)[7]、正交匹配追踪(OMP)[9]等,贪婪方法需要的测量数m较多,而且恢复精度相对不高[14].
Candes等提出了受限等距性(restricted isometric property,RIP)的概念[15].对于任意常数K=1,2…,矩阵θ的受限等距常数δk为使式(6)成立的最小数:

式中:s为任意的k-稀疏向量.
若δk≪1,则称测量满足RIP性质.当测量满足RIP性质时,可以将重构问题转化为l1范数最小化.而l1范数最小化是一个凸优化问题,Lasso[10]、最小角度回归(LARS)[11]等多种稀疏重构算法都可以解决.
2 基于压缩感知的时变信号压缩
含噪时变信号可以由压缩信号y表示为

式中:z为随机噪声;x(t)为原始信号.
在机械振动信号中,原始时变信号x(t)在时域内一般是非稀疏的,因此,θ=Φφ.本文算法流程如图1所示.
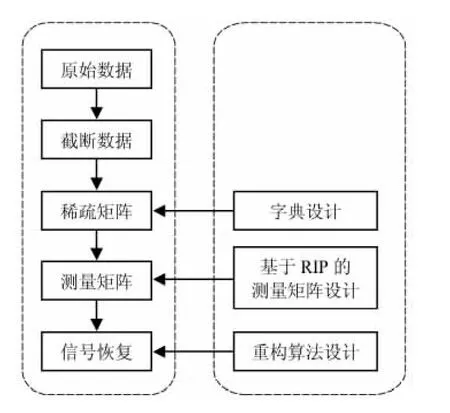
图1 算法流程Fig.1 Flow chart of TvCS algorithm
2.1 基于DFT的稀疏矩阵设计
信号x(t)的稀疏性或可压缩性是压缩感知的重要前提[16],因此,压缩感知的首要研究任务就是信号的稀疏表示.傅里叶变换可以有效地稀疏表示振荡时变信号,离散傅里叶变换(discrete fourier transform,DFT)是傅里叶变换在时域和频率都呈离散的形式,将信号的时域采样变换为其DFT的频率采样.对于 N 点序列{x[n]}0≤n≤N,它的离散傅里叶变换为
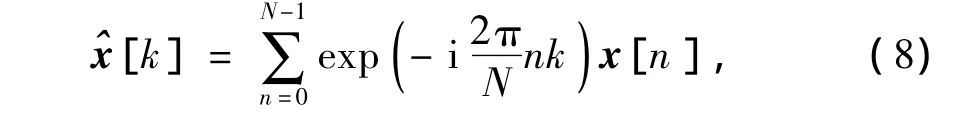
2.2 测量矩阵设计
测量矩阵的设计直接影响信号的压缩率和信号的重构精度.独立同分布地从均值为零、方差为1/M的正态分布生成测量矩阵 Φ,即 φi∈(0,1/M).由RIP准则可知,当测量数据满足不等式(9),压缩信号能够完整地被重构.

式中:M为测量个数;C为常数;K为稀疏系数;N为原始信号长度.
2.3 基于Lasso的重构算法
因为原始信号x在稀疏域上具有稀疏性,基于Lasso的信号重构算法可以转化为以下优化问题:
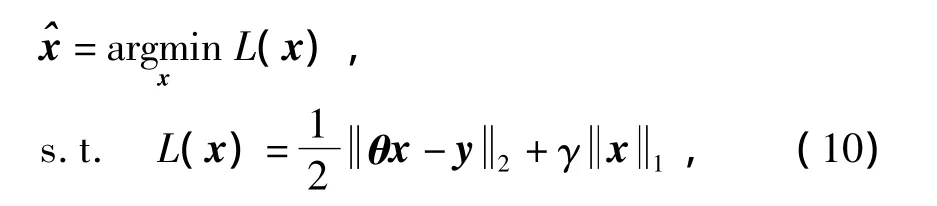
式中:γ>0为正则项参数,控制重构信号 ^x的稀疏度.
由式(10)可知,Lasso参数估计是一个非线性和非可微的函数,因此很难通过最小二乘法取得准确解.本文中,采用坐标下降(coordinate descent)算法进行求解,坐标下降算法的思想是在多维变量情况下固定其它所有维向量,仅进行一维处理.
2.4 算法设计
基于压缩感知的时变信号压缩与重构算法流程有以下几步:
(1)信号稀疏:利用DFT矩阵变换原始信号s,得到原始信号在DFT矩阵空间内的稀疏信号x;
(2)信号测量:选择合适的随机测量矩阵Φ,计算稀疏信号在测量矩阵下的压缩表示y=Φx;
(3)信号重构:信号采集过程满足RIP性质,通过Lasso算法重构出原始信号^x;
(4)信号恢复:在重构稀疏信号^x上乘以DFT稀疏变换矩阵,恢复出原始信号^s.
3 仿真实验
为验证提出算法对时变信号的压缩和去噪性能,本文进行了如下实验,分别通过对时域稀疏信号、无噪声非时域稀疏信号和含噪声非时域稀疏信号运用小波压缩方法和TvCS算法进行压缩与重构实验,比较2种方法的压缩重构效果和去噪能力.本文的仿真硬件环境为AMD 3.0 GHz处理器,内存为4 GB,操作系统为Windows7.软件环境平台为MATLAB R2012a.
3.1 时域稀疏信号
机械装备中,当某个零件出现松动、脱落后将会产生冲击信号,一定条件下,冲击信号呈现一定的时域稀疏性.为研究提出算法对时域稀疏时变信号的压缩性能,随机生成一个信号长度N=512的稀疏信号.由于信号在时域是稀疏的,采样过程中只需测量矩阵对原始信号进行采样,试验中两种算法的压缩比均取为50%.小波压缩重构算法采用Morlet小波作为母小波进行小波包分解,分解层数为3层.采用Huffman编码对系数记性编码.图2中,f指原始信号,xp指TvCS算法重构信号,sd指小波压缩重构信号.RMSE1:0.000 025是原始信号与TvCS算法重构信号之间的均方根误差,RMSE2:4.502 514是原始信号与小波压缩重构信号之间的均方根误差.试验结果表明,在同等压缩比的情况下,TvCS算法的信号重构能力要好于小波压缩重构算法.上文RMSE的计算式为
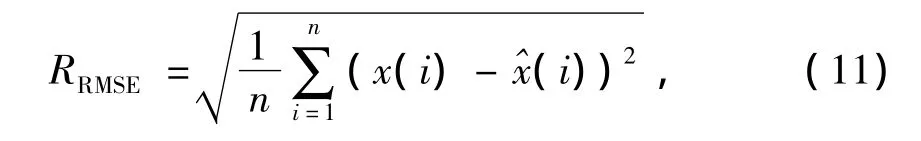
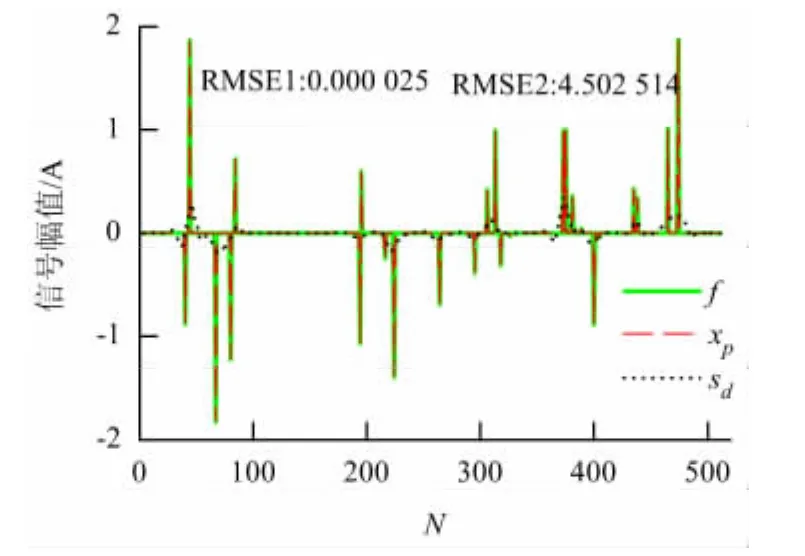
图2 时域稀疏信号的压缩与重构Fig.2 Compression and reconstruction of time-domain sparse signal
3.2 非时域稀疏无噪声信号
为更近一步说明本文算法的时变信号压缩能力,选择非时域稀疏信号作为测试信号,对提出的算法进行实验,测试信号长度N=102 4.信号是以3.4和9.1 Hz为基频的正弦及其各次谐波的线性叠加,表达式如下:

频域稀疏信号的压缩与重构如图3所示.
由图3可知,小波压缩重构信号与原始信号之间的均方根误差为0.260 2,本文提出算法的均方根误差为0.142 0.由此可知,对于非时域稀疏无噪声信号,TvCS算法的信号重构能力要好于小波压缩重构算法.
为研究提出算法压缩比例对信号恢复的影响,本文进行如下对比实验.在不同的压缩比下分别测试相应重构信号与原始信号的均方根误差.实验结果如图4所示.由图可知,随着采样原子的个数增加(压缩比例减小),算法的信号恢复能力逐渐增强.当压缩比例为25%时,算法的信号恢复能力基本趋于稳定,RMSE达到0.25左右.
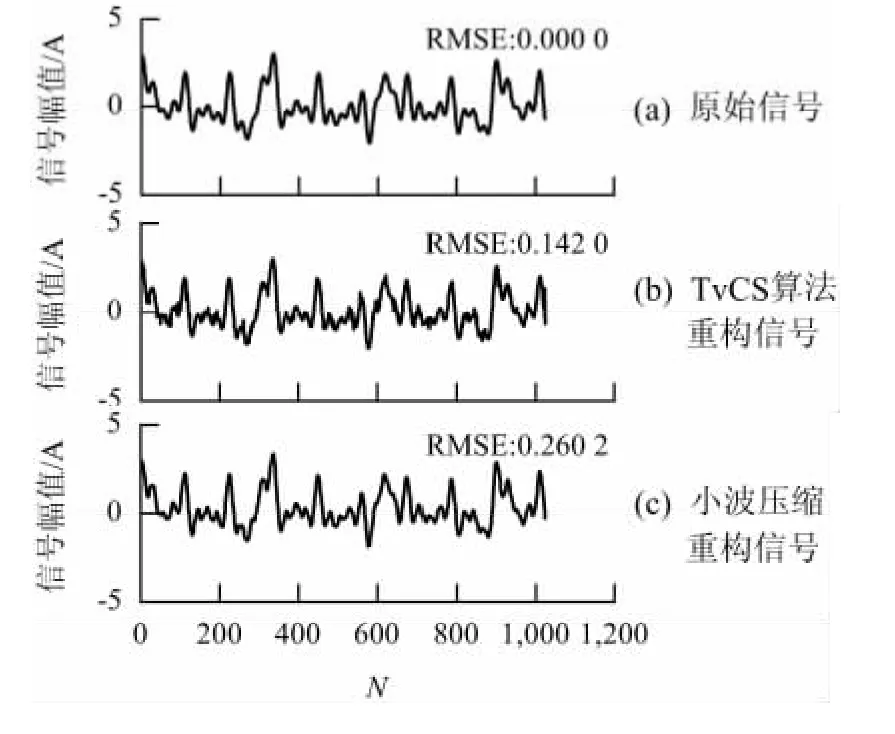
图3 频域稀疏信号的压缩与重构Fig.3 Compression and reconstruction of frequency-domain sparse signal
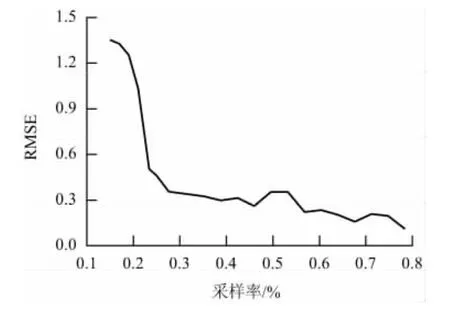
图4 压缩率与重构信号均方根误差关系Fig.4 Relationship between compression rate and RMSE of the reconstructed signal
3.3 非时域稀疏含噪信号
工业现场工况复杂,采集的数据往往是振动信号和噪声的混合信号[17].因此,为验证提出的算法对于含噪声信号的压缩和去噪能力,本文进行了如下实验进行验证:
在实验信号中加入随机噪声z,即信号表达式变为
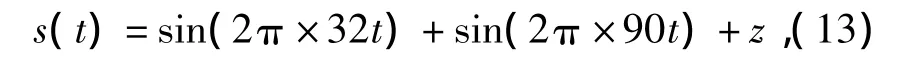
式中:z∈N(0,t).在原始信号有噪声情况下,压缩感知的优化问题变为
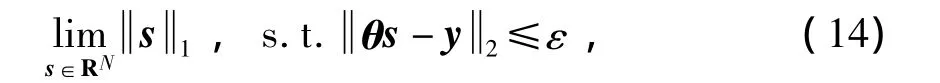
式中:ε为误差项.
图5中,由上至下分别是非时域稀疏含噪信号、本文算法压缩重构信号和小波压缩重构信号.本文提出的算法选取DFT矩阵为稀疏矩阵,随机矩阵为测量矩阵,重构算法采用基于l1范数最小化的Lasso算法.信号长度为N=1 024,稀疏性为256,松弛稀疏为1×10-5.小波压缩算法中,小波基函数为Morlet小波,对原始信号进行3层分解.选用全局阀值进行信号的压缩处理,阀值取为40.由图5可知,在当前参数条件下,本文算法重构后的信号与未加入噪声的原始信号之间的RMSE为0.545 1,信噪比(RNS)为 -23.801 1.而小波压缩重构后的信号与未加入噪声的原始信号之间的RMSE 为0.864 3,信噪比 RNS 为 -24.033 3.结果表明,本文提出的方法相对于小波重构的方法压缩性能好,并且有较强的去噪能力.
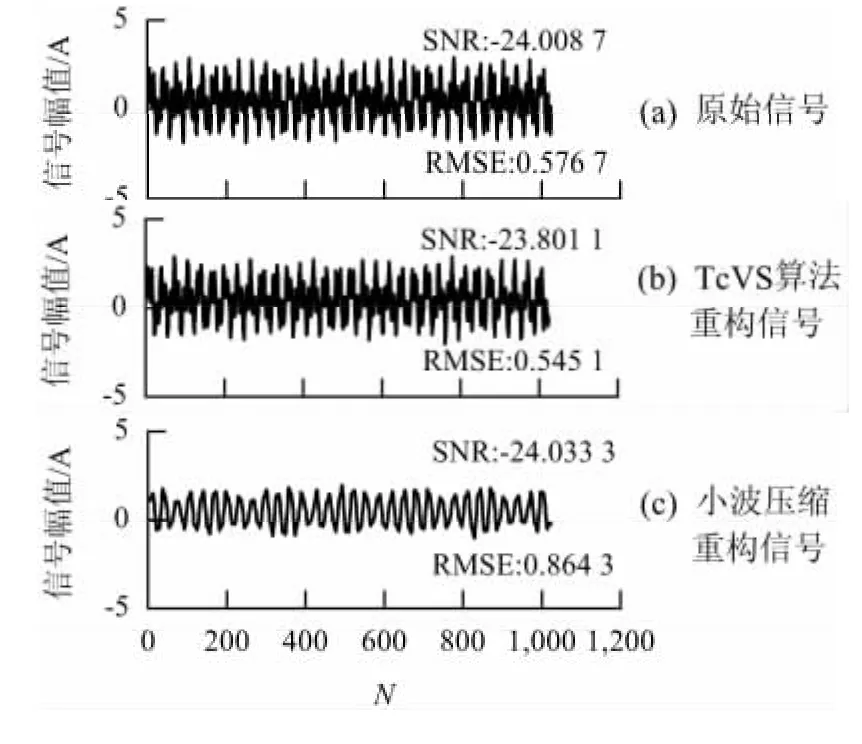
图5 频域稀疏含噪信号的压缩与重构Fig.5 Compression and reconstruction of frequency-domain sparse signal tainted by noise
4 实验分析
4.1 实验设备
为进一步验证TvCS的有效性和实用性,在长征718机床上采集主轴系统正常状态振动信号并进行实验,实验系统如图6所示.

图6 试验平台示意图Fig.6 Schematic of experimental platform
在图6中,主轴系统前端安装INV9832型加速度振动传感器,监测主轴系统状态.振动信号经过INV1870型调理仪调理后,由PCI-1710采集卡采集至工控机.振动信号采样频率为10 kHz,采样持续时间20 s.
4.2 算法验证
为验证本文算法TvCS的有效性,将TvCS与小波压缩进行对比.图7分别正常工作状态下不同压缩比的保留能量百分比和均方根误差的关系.

图7 压缩比与均方根误差和保留能量百分比关系Fig.7 Compression rate vs RMSE and energy retention rate
由图7可以看出,在同样压缩比的情况下,TvCS比小波的压缩效果要好,TvCS更能保障振动信号的质量.设置压缩比为45%,比较两种在此压缩比下的重构信号,如图8所示.图8由上至下分别为原始信号、TvCS压缩重构信号、小波压缩重构信号.由图8可以看出,TvCS的重构RMSE为4.6×10-6,小波压缩的重构 RMSE 为6.6 ×10-6.
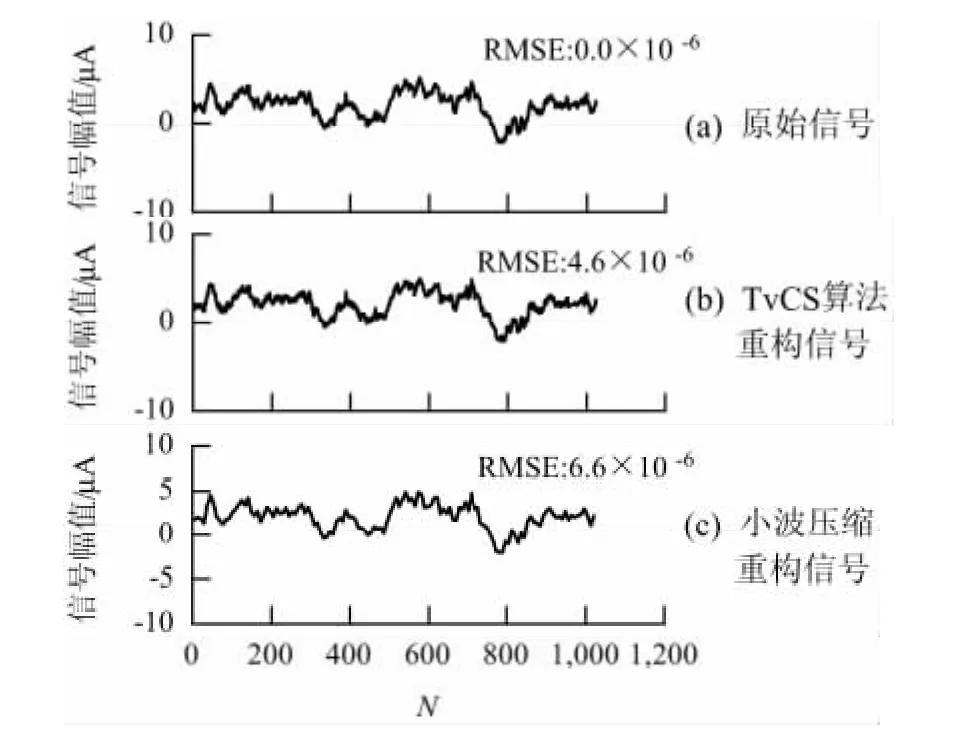
图8 对主轴振动信号通过不同压缩算法的重构信号Fig.8 Spindle vibration signals reconstructed by different algorithms
5 结论
本文以机械振动时变信号为研究对象,以压缩感知技术为理论基础,构造了稀疏矩阵和信号感知矩阵,实现了原始信号的压缩,最后通过优化求解的方法对原始信号进行重构.理论和实验结果表明,本文提出的方法对于时变信号具有很好的压缩能力,并且能够有效地去除信号中的噪声成分.本文算法可应用于机械振动信号的采集、远程传输和信号去噪等工程实践.
[1]赵贻玖.稀疏模拟信号压缩采样与重构算法研究[D].成都:电子科技大学,2012.
[2]马晓建,陈瑞琪.机械装备中跌落物冲击信号的恢复[J].振动与冲击,2001,20(1):31-33.
MA Xiaojian,CHEN Ruiqi.The recovery of falling part impact signal in mechanical equipment[J].Journal of Vibration and Shock,2001,20(1):31-33.
[3]CHEN X,DU Z,LI J,et al.Compressed sensing based on dictionary learning for extracting impulse components[J].Signal Processing,2014,96:94-109.
[4]DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[5]CANDES E J,ROMBERG J K,TAO T.Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics,2006,59(8):1207-1223.
[6]CHEN W, WASSELL I J. Energy-efficient signal acquisition in wireless sensor networks:a compressive sensing framework[J].IET Wireless Sensor Systems,2012,2(1):1-8.
[7]MAMAGHANIAN H,KHALED N,ATIENZA D,et al.Compressed sensing for real-time energy-efficient ECG compression on wireless body sensor nodes[J].IEEE Transactions on Biomedical Engineering, 2011,58(9):2456-2466.
[8]闫斌,陈浩,王文东,等.一种基于盲运算的1比特压缩感知重建算法[J].西南交通大学学报,2015,50(2):264-269.
YAN Bin,CHEN Hao,WANG Wendong,et al.1 bit compressed sensing reconstruction algorithm based on blind operation[J].Journal of Southwest Jiaotong University,2015,50(2):264-269.
[9]LI S,DA X L,WANG X.Compressed sensing signal and data acquisition in wireless sensor networks and internet of things[J].IEEE Transactions on Industrial Informatics,2013,9(4):2177-2186.
[10]TIBSHIRANI R.Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society,1996,58(1):267-288.
[11]DAVENPORT M A,BOUFOUNOS P T,WAKIN M B, et al. Signal processing with compressive measurements[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):445-460.
[12]CHEN F,CHANDRAKASAN A P,STOJANOVIC V.A signal-agnostic compressed sensing acquisition system for wireless and implantable sensors[C]∥Custom Integrated Circuits Conference(CICC).[S.l.]:IEEE,2010:1-4.
[13]MASIERO R,QUER G,MUNARETTO D,et al.Data acquisition through jointcompressive sensing and principal component analysis[C]∥ Global Telecommunications Conference,2009.[S.l.]:IEEE,2009:1-6.
[14]GURBUZ A C,MCCLELLAN J H,SCOTT W R.A compressive sensing data acquisition and imaging method for stepped frequency GPRs[J]. IEEE Transactions on Signal Processing,2009,57(7):2640-2650.
[15]CANDES E J.The restricted isometry property and its implicationsforcompressed sensing[J]. Comptes Rendus Mathematique,2008,346(9):589-592.
[16]DO T T,GAN L,NGUYEN N,et al.Sparsity adaptive matching pursuitalgorithm forpractical compressed sensing[C]∥42nd Asilomar Conference on,Signals,Systems and Computers.[S.l.]:IEEE,2008:581-587.
[17]高宏力,李登万,许明恒.基于人工智能的丝杠寿命预测技术[J].西南交通大学学报,2010,45(5):685-691.
GAO Hongli,LI Dengwan,XU Mingheng.Intelligent monitroing system for screw life evaluation[J].Journal of Southwest Jiaotong University,2010,45(5):685-691.

