混沌最小二乘支持向量机的短期风功率预测*
邱 杰,裴瑞平,张安川,李 侃
(安徽工程大学电气工程学院,安徽芜湖 241000)
混沌最小二乘支持向量机的短期风功率预测*
邱 杰,裴瑞平**,张安川,李 侃
(安徽工程大学电气工程学院,安徽芜湖 241000)
结合混沌的相空间重构理论和LS-SVM的优点,提出了一种基于混沌LS-SVM风功率预测方法,利用误差评价函数形成反馈机制,通过误差反馈建立参数合理的风功率预测模型;通过对实际数据的仿真,结果表明所提出的混沌LS-SVM预测模型有较好的非线性拟合能力,有较高的预测精度。
混沌;LS-SVM;风功率预测;相空间重构
全球性的能源短缺和突出的环境问题,驱动着新能源的迅速发展。风能是一种可再生的、清洁的能源,被世界各国广泛用来发电,风力发电也得到了迅猛的发展。由于风力具有间歇性和随机性,风电的大规模并网给电网带来很大的冲击,严重影响着电网的安全稳定运行。准确的预测风功率,有利于电力系统调度部门制定合理的调度计划,减轻风电对电网的不利影响。因此,进行风功率预测具有重要的意义。
风能是一种自然资源,具有一定的自然规律性,同时受纬度、海拔、地形、气压、温度等因素的影响又有很强的随机性。因此,风力发电系统是一个复杂的非线性系统,具有混沌特性,而混沌时间序列在短期内是可以预测的[1]。可以利用混沌的相空间重构理论,研究风功率时间序列的非线性动力特性,它支持向量机具有学习速度快、泛化能力好的优点,能解决好小样本、非线性、高维数和局部极小值等问题[2]。因此,将结合混沌和支持向量两者的优点,建立基于混沌最小二乘支持向量机的风功率预测模型,对风功率进行预测。
1 相空间重构理论
Taken指出,在一维观测序列及其适当延时值所构成的维数合适的相空间中,系统演化的动力学行为可由此空间中点的演化轨迹无奇异的表达出来,这个观测值及其延时值所构成的空间称为重构相空间[3]。通过重构相空间,可以在高维空间中恢复混沌吸引子,混沌吸引子作为混沌系统的特征之一,体现着混沌系统的规律性[1]。非线性动力学系统的状态都可由多个分量进行描述,且各分量之间具有相互作用,因此任一分量的演变过程中隐含着相关分量的信息。这样,可通过对一个分量的观测时间序列进行重构来恢复和提取系统固有的规律性。
在风功率系统中,设风功率序列为:{x(ti)|i=1,2,…,n},当嵌入维数为m,时间延迟为τ,相空间中相点个数为N=n=(m-1)τ时,重构的相空间向量{Xj|j=1,2,…N}为
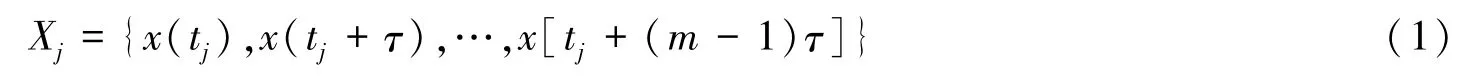
则N个重构的相空间向量描述了系统在相空间的演化轨迹。
2 LS-SVM模型
LS-SVM是将SVM[4]中的不等式约束改为等式约束,把求解二次规划问题转化为求解线性方程组问题,从而提高求解问题的速度和收敛精度[2,5]。
设样本为m维向量,有l个样本可表示为(x1,y1),(x2,y2),…,(xl,yl)。首先用一个非线性映射φ(·)把样本从原空间Rm映射到特征空间φ(xi),在这个高维特征空间中构造最优决策函数:

将非线性估计函数转化为高维特征空间的线性估计函数。LS-SVM的优化问题为

式(4)中ξi为松弛因子。用拉格朗日法求解问题,得:
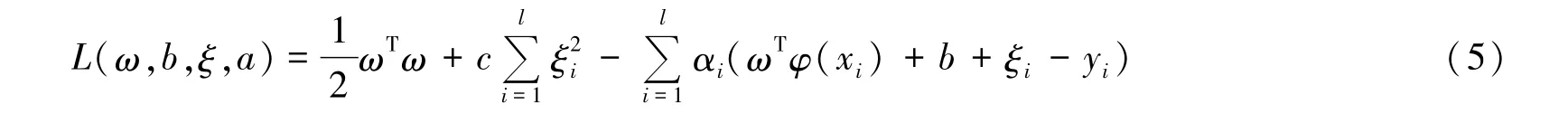
式(5)中αi(i=1,2,…,l)是拉格朗日乘子。
根据优化条件:
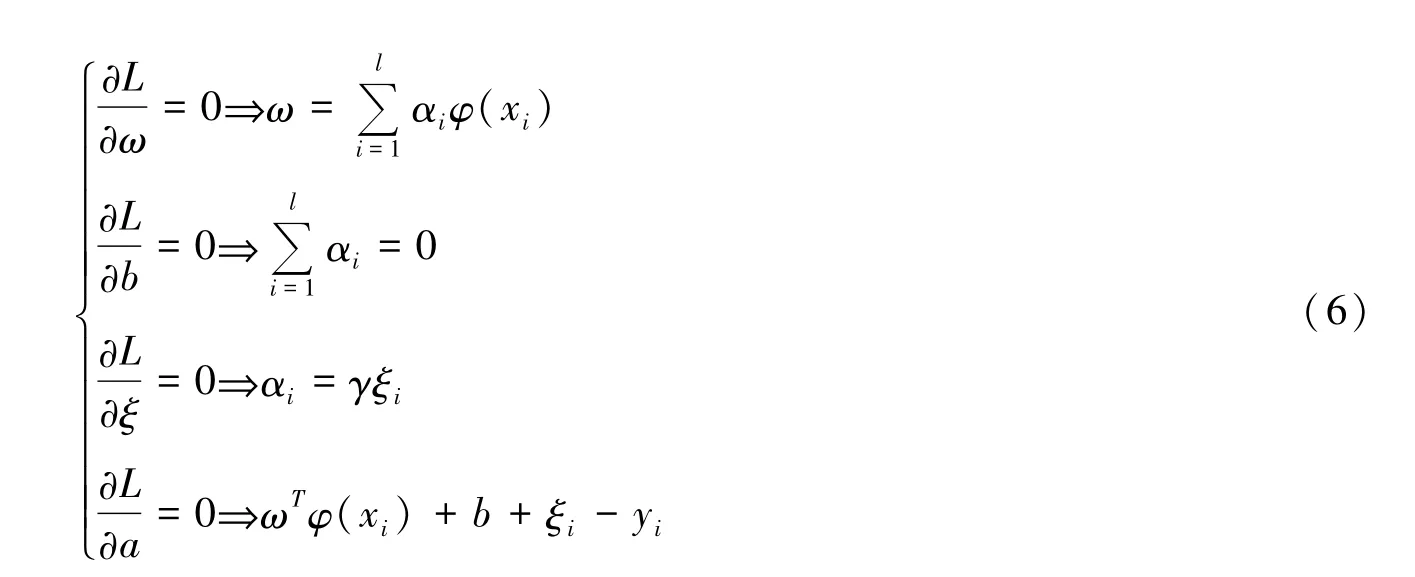
消去式(6)中的ω和ξ可得:
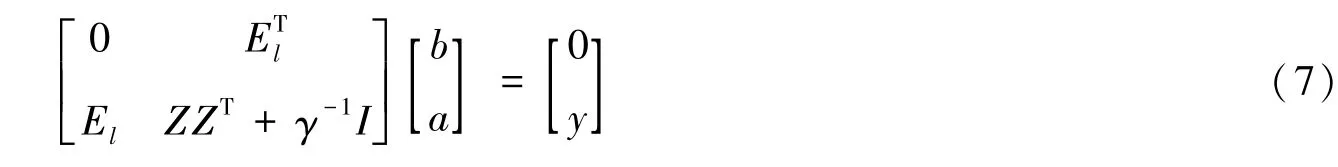
式(7)中:El=[1,1,…1]T,Z=[φ(x1),φ(x2),…,φ(xl)]T,y=[y1,y2,…yl]T,a=[a1,a2,…al]T。为了解决高维计算问题,通常采用核函数K(x,xi)来代替内积计算φ(xi)Tφ(xj)。通过求解式(7)可得LS-SVM回归函数:

3 混沌LS-SVM预测流程
3.1 归一化预处理
为避免样本数据的偏大和偏小数据对预测精度的影响,通常都有对样本进行归一化的预处理,使数据在[0,1]区间。设xmin为样本中最小的数据值,xmax为样本中最大的数据值,那么对于任一样本值x,其归一化数值为

对归一化后的预测结果y′,其对于的预测实际值为

3.2 参数设置
利用混沌的相空间重构理论进行重构时,需要选择恰当的延迟时间τ和嵌入维数m。通常,用于确定延迟时间的方法有:自相关函数法、互信息法和经验法则等,用于确定嵌入维数的方法有:G-P算法、Cao方法等[3]。
常用的核函数有多项式核函数、径向基核函数、Sigmoid核函数[6]。选用径向基核函数:

核函数的参数可以用网格搜索法[5]确定。
3.3 误差评价
为了检测模型的预测效果,需要选择评价函数,这里选用:平均绝对误差MAE和平均绝对百分比误差MAPE来评价预测结果,即:

N为测试样本数;yi为预测序列的真实值;y′i为预测值。
3.4 预测流程
对历史数据进行挑选,并剔除错误的数据,然后进行归一化处理;设置延迟时间和嵌入维数和核函数参数;将混沌重构的相点分为训练样本和测试样本用来训练和测试LS-SVM预测模型;利用误差评价函数,评价预测模型;根据预测误差调整参数,直至预测误差最小为止,即建立了合理的预测模型,输出预测结果,其预测流程见图1。

4 实例分析
选用某风电场的2006年5-6月的历史风功率数据共2 000个数据点,其中1 500个数据点作为训练数据,对模型进行训练;500个数据点作为测试样本,用来对预测模型进行测试。采用Matlab7.1建立预测模型,当参数τ=2,m=6,γ=116,δ=0.012时,预测误差MAPE=15.76%最小。当分别采用LS-SVM模型和所建立的混沌LS-SVM模型对2006年6月3日的风功率进行预测时的结果见图2,两者的误差见表1,由图2、表1可知,所建立的混沌LS-SVM的有较好的非线性拟合能力,有较高的预测精度。

图2 LS-SVM和混沌LS-SVM预测曲线

表1 LS-SVM和混沌LS-SVM预测误差
5 结 论
结合混沌的相空间重构理论和LS-SVM的优点,提出了一种基于混沌LS-SVM风功率预测方法,通过误差评价函数对预测结果的评价,形成误差反馈机制来调整预测模型的参数,最终建立参数合理的预测模型。通过对实际历史风功率数据的仿真研究,表明所提出的混沌LS-SVM较LS-SVM预测模型,取得了较好的预测效果,有更高的预测精度。
[1]李玲玲,李俊豪,王成山,等.基于混沌支持向量机的短期风速预测[J].低压电器,2012,16:48-52
[2]王晓兰,王明伟.基于小波分解和最小二乘支持向量机的短期风速预测[J].电网技术,2010,34(1):179-184
[3]张淑清,贾健,高敏,等.混沌时间序列重构相空间参数选取研究[J].物理学报,2010,59(3):1576-1582
[4]田丽,曹安照,王蒙,等.基于SVM和神经网络的组合预测模型物流需求预测[J].重庆工商大学学报:自然科学版,2012,29(9):61-69
[5]杜颖,卢继平,李青,等.基于最小二乘支持向量机的风电场短期风速预测[J].电网技术,2008,32(10):62-66
[6]戚双斌,王维庆,张新燕.基于SVM的风速风功率预测模型[J].可再生能源,2010,28(4):25-32
[7]卢振利.相空间重构和正则极限学习机的网络流量预测[J].激光杂志,2015,36(1):109-113
Short-term Wind Power Forecasting Based on Chaotic LS-SVM
QIU Jie,PEI Rui-ping,ZHANG An-chuan,LI Kan
(School of Electric Engineering,Anhui Polytechnic University,Anhui Wuhu 241000,China)
In combination of phase space reconstruction theory and the advantage of LS-SVM,this paper proposes a kind of forecasting method for wind power based on chaotic LS-SVM,making use of the feedback mechanism of error evaluation function.By the feed back mechanism,wind power model with reasonable parameters is designed.The simulation results show that the proposed forecasting model has better nonlinear fitting capability and more precise forecasting.
chaotic;LS-SVM;wind power forecasting;phase-space reconstruction
TP399
A
1672-058X(2015)03-0047-04
10.16055/j.issn.1672-058X.2015.0003.010
2014-07-18;
2014-09-18.
安徽省级大学生创新创业训练计划项目(AH201310363228);安徽工程大学青年基金项目(2013YQ35).
邱杰(1991-),男,安徽六安人,从事电力系统仿真研究.
**通讯作者:裴瑞平(1979-),女,河南武陟人,讲师,硕士,从事复杂系统建模仿真研究.E-mail:sendypei@163.com

