一种新的三维表面重构方法
杨昆朋,张荣国,刘 霞,刘小君
(1.太原科技大学计算机科学与技术学院,太原 030024;2.邢台学院数学与信息技术学院,河北邢台054001; 3.合肥工业大学机械与汽车工程学院,合肥 230009)
一种新的三维表面重构方法
杨昆朋1,张荣国1,刘 霞2,刘小君3
(1.太原科技大学计算机科学与技术学院,太原 030024;2.邢台学院数学与信息技术学院,河北邢台054001; 3.合肥工业大学机械与汽车工程学院,合肥 230009)
针对CT图像,给出了一种三维表面重构的方法。首先用中值滤波的方法进行预处理后,根据曲率信息提取轮廓线上的特征点,然后按照最短对角线法进行连接,其中在选取上下轮廓线两点间最短距离时,采用欧式距离进行实现,同时为了使构造的三角形视觉效果较好,分别计算当前点角的余弦值,从中选择较小的。最后将该方法与原方法分别进行实验,验证了使用部分轮廓特征点也能实现三维表面重构,重构效果较为满意。
CT;轮廓线;曲率;最短对角线
三维表面重构技术中主要两类不同的方法实现:体绘制和面绘制。由于体绘制的计算量偏大,而且对图像计算和显示的硬件要求比较高。因此都采用面绘制的方法进行三维表面重构。主要方法有Lorensen[1]在1987年提出了移动立方体(marching cubes,MC)算法。MC采用等值面的思想,用三角形拟合一定灰度阈值的等值面。但MC算法在生成曲面的时候很容易产生二义性问题,因此针对这个问题,很多人对此做了大量的改进。张荣国等[2]提出基于共轭梯度的B样条主动轮廓边缘提取方法。王庆霞等[3]根据四叉树结构的层次化模型简化生成三维地形网格,钱苏斌[4]提出用行扫描线法提取带孔的轮廓线,再结合最小对角线完成三角面片的连接,姚民仓等[5]为解决轮廓线的分支问题,提出了改进的最短对角线法,李运锋等[6]针对轮廓线拼接的复杂性,提出方向包围盒的方法进行轮廓点的拼接,最后用最短对角线法实现表面的重构。然而这些方法都采用了轮廓线上的所有像素点,然而在重构表面时,有些却不是必须的。
因此,在获得物体的轮廓线之后,根据曲率的大小选择合适的像素点,然后采用改进的最短对角线法进行三维表面的重构。
1 轮廓线的提取及三维重构
1.1 CT预处理
在获取CT切片的过程中,由于各种因素的影响,使得图像中存在一定的噪声,图像中目标物体部分边缘也可能局部不清晰。因此在获得图像的二值图像后,采用水平集中Chan-Vase图像分割模型的方法(式1)对感兴趣的区域进行提取:
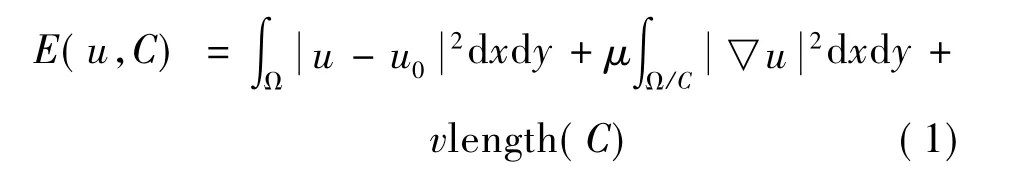
其中,μ、v是非负常数代表各能量项的权重系统,μ0是初始图像,u是逼近初始图像μ0的一个分段图像,Ω是图像I(x,y)定义的区域,C是分割前景和背景区域的边界曲线。
1.2 轮廓点提取与精简
通过上述方法在获得CT图像的轮廓线之后,然后再采用逐行扫描的方法对轮廓线进行扫描,获
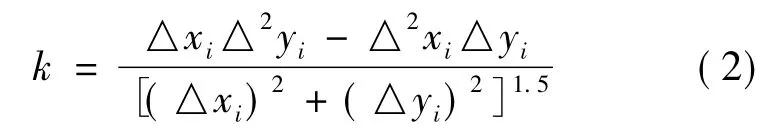
1.3 三维重构
轮廓线连接表面重构自70年代提出以来,有许多人从不同的角度提出了各种算法,如最小表面积法、最大体积法、同步前进法、最短对角线法等。由于最短对角线法具有简单、容易实现,而且当上下两条轮廓线的大小和形状相近,相互对中情况效果是比较好的。
在相邻两条轮廓线中,设上层轮廓线上的点和下层轮廓线上的点分别表示为:Ci={p(i),i=1,2,…m} Ci+1={q(j),j=1,2,…n},如图1所示,设Pi是上层轮廓线Ci上的任意一点,在下层轮廓线Ci+1上找到距离Pi最小的像素点,设为Qj,则以跨距PiQj为基础,如果PiQj+1<Pi+1Qj,则连接Pi,Qj+1形成三角面片。得其像素点。由于每一条轮廓线线上都由许多的像素点构成,然而在进行三维表面重构的时候并不是需要所有的轮廓线上的像素点,因此采用文献[7]中的方法对轮廓线上的特征点进行精简,进而获得该像素点在直角坐标系下的二维坐标值。
采用文献[7]中曲率的计算方法,具体如下:

图1 最短对角线法示意图Fig.1 The shortest diagonal method
在计算得到各个像素点的曲率值之后,人工进行选取适当的范围,使符合条件的像素点都落在选取的区间中。
采用最短对角线法连接三角面片时,在选取上下两条轮廓线两点间的最短距离时,采用公式(3)欧式距离进行选择。
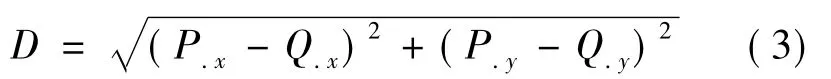
其中Q.x、Q.y分别表示当前像素点的坐标值,P.x、P.y分别表示离当前点最近的坐标值。同时为了在三角化的过程中,取得较好的视觉效果,使构造的三角形尽量为锐角三角形,避免出现如图2中的情况:
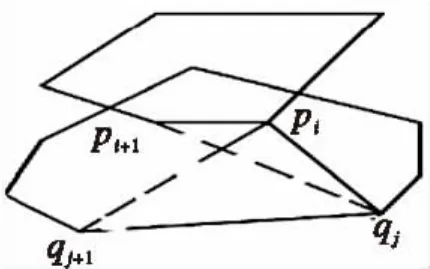
图2 最短对角线中一种特殊情况Fig.2 A special case of the shortest diagonal
因此分别计算∠piqjpi+1和∠qjpipi+1的余弦值,如果前者小于后者,则连接pi、qj+1,否则连接pi+1、qj.同时根据其欧式距离的大小来选择上下轮廓线中距离最短的像素点,在连接像素点构造三角面片时,采用Delaunay三角网逐点插入的方法构造,采用如下所示的数据结构:
(1)点数据结构,用于存储像素点的坐标,其定义如下:
typedef struct{double x,y,z;像素点 x,y,z坐标}POINT3D
(2)三角形数据结构,用于存储三角形三个顶点,其定义如下:
typedef struct{POINT3D p[3];三角片三个顶点的坐标}TRIANGLE
采用此方法把所有的CT轮廓线进行连接之后,构造出三角网格模型,同时借助于OpenGL开放式三维环境,对构成的三维网格进行光照渲染等处理。
2 其算法的具体实现步骤
根据最短对角线法进行三维表面重构的具体算法步骤如下:
(1)利用公式(1)获得CT的轮廓线,并把获得的像素点的坐标值存入二维数组中;
(2)根据公式(2)计算各个像素点的曲率值,并把符合设置曲率区间的像素点的坐标值保存到另一二维数组中;
(3)在上轮廓线Ci中选择一点Pi,并在下轮廓线Ci+1中选择一点Qj,在选择点Pi+1还是选择Qj+1时,根据公式(3)分别计算其欧式距离D(PiQj+1)、D(QjPi+1),并人工设置阈值范围 T,同时计算∠piqjpi+1和 ∠qjpipi+1,如果 D(PiQj+1) < T 且∠qjpipi+1的余弦值小于∠piqjpi+1,则保留并连接三角形△PiQjQj+1,否则连接△PiPi+1Qj;
(4)重复(3),当某条轮廓线上只剩下最后一个点时,另一条轮廓线上的点都与这个点进行连接,直到把所有点都连入三角形为止。
(5)直到把所有的轮廓线处理完,构造出三角网格模型。
3 实验结果及讨论
实验平台:Intel(R)Pentium(R)CPU,主频为2.13GHZ,内存为2GB,操作系统为Windows 7,软件环境:VS2008结合OpenGL,搭建应用平台。选取曲率的范围为[-0.1,0.1]之间。对大小为256×256的CT断层图像进行三维表面重构实验。采用原始图像Head 183张CT切片,其中图3为感兴趣区域,图5(a)、图6(a)表面重构,图5(b)、图6(b)侧面效果图,图5(c)、图6(c)为加入光照后的三维表面;采用原始图像Shoulder 166张CT切片,其中图7为感兴趣区域,图9(a)、图10(a)表面重构,图9 (b)、图10(b)侧面效果图,图9(c)、图10(c)加入光照后的三维表面。其中图4(a)为采用Head图像上的所有像素点,4(b)为精简后的像素点,图8 (a)为采用Head图像上的所有像素点,8(b)为精简后的像素点,不同方法的比较见表1.
其中PR=(原始点数-精简后的点数)/原始点数。

图3 Head感兴趣区域Fig.3 Head interested region
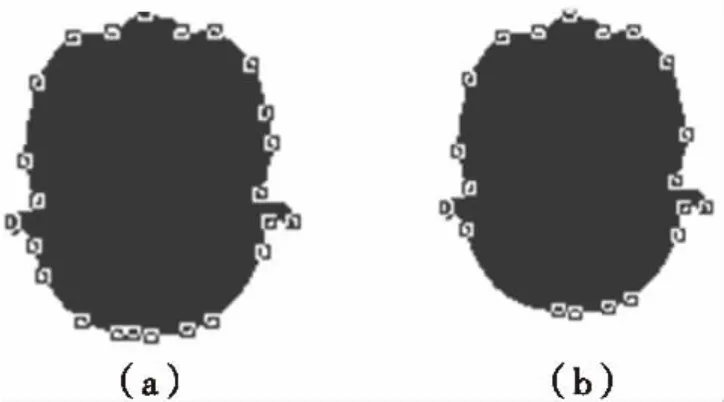
图4 Head像素点精简前后Fig.4 The pixels of Head pixels before and after streamline
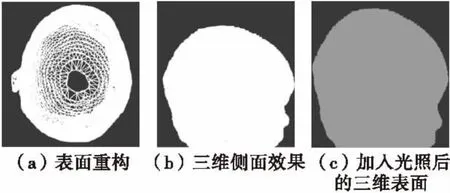
图5 Head三维表面重构(本方法)Fig.5 Head 3d surface reconstruction(The method in this study)

图6 Head三维表面重构(原方法)Fig.6 Head 3d surface reconstruction(The original method)
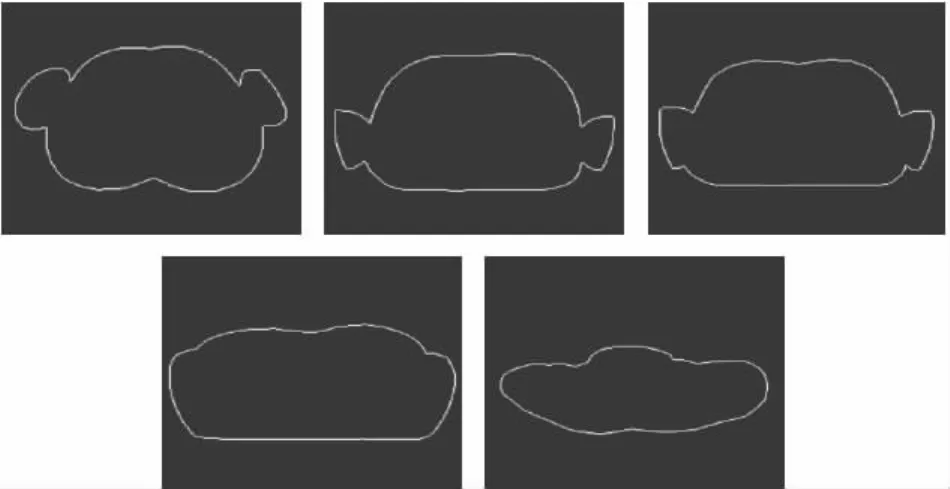
图7 Shoulder感兴趣区域Fig.7 Shoulder interested region
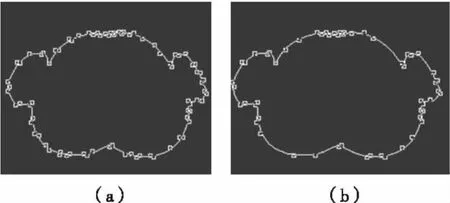
图8 Shoulder像素点精简前后Fig.8 The pixels of Shoulder before and after streamline
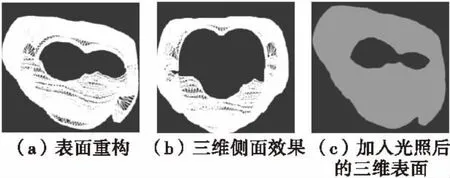
图9 Shoulder三维表面重构(本方法)Fig.9 Shoulder 3D surface reconstruction (The method in this study)

表1 不同方法的比较Tab.1 The comparison of different methods

图10 Shoulder三维表面重构(原方法)Fig.10 Shoulder 3D surface reconstruction (The original method)
4 结束语
通过对轮廓线上的像素点采用曲率进行特征点的提取,然后设置曲率区间从中选择适当的像素点,最后用最短对角线法进行三维表面重构。实验证明,使用部分像素点用该方法也能重构三维表面,而且通过使用这两种方法分别进行三维表面重构来看,其效果也较为满意。
[1]CLINE H E,LORENSEN W E,LUDKE S,et al.Two algorithms for the three-dimensional reconstruction of tomograms[J].Medical physics,1988,15(3):320-327.
[2]张荣国,刘小君,刘焜,等.基于共轭梯度的B样条主动轮廓边缘提取[J].中国图象图学学报,2010,15(1):103-108.
[3]王庆霞,张荣国,武妍,等.四叉树结构地形网格简化算法的研究[J].太原科技大学学报,2013,34(1):1-5.
[4]钱苏斌.基于轮廓线的任意形体三维重建[J].成都大学学报:自然科学版,2013,32(3):262-266.
[5]姚民仓,秦新强,胡钢.由断层图像轮廓重构三维表面的新算法[J].微计算机信息,2009(25):214-216.
[6]李运锋,刘修国.基于方向包围盒投影转换的轮廓线拼接算法[J].计算机应用,2011,31(12):3353-3356.
[7]HE X C,YUNG N H C.Corner detector based on global and local curvature properties[J].Optical Engineering,2008,47(5): 8-12.
A New Method of 3d Surface Reconstruction
YANG Kun-peng1,ZHANG Rong-guo1,LIU Xia2,LIU Xiao-jun3
(1.School of Computer Science and Technology,Taiyuan University of Science and Technology,Taiyuan 030024,China;2.School of Mathematics and Information Technology,Xingtai University,Heibei Xingtai 054001,China; 3.School of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei 230009,China)
a method of 3d surface reconstruction for CT images was proposed.The feature points on the contour are extracted based on the curvature information.Then feature points are connected based on the shortest diagonal method.When selecting the shortest distance between the up and down contour points,euclidean distance was used to achieve.At the same time,the smaller current point angle was choosen to make the structure of the triangular visual effected better.Finally,the experiments verified that using partial contour feature points also can realize 3d surface reconstruction,and the result is satisfactory.
CT,contour,curvature,the shortest diagonal
TP391
A
10.3969/j.issn.1673-2057.2015.04.009
1673-2057(2015)04-0284-04
2014-12-29
国家自然基金(51375132);山西省自然基金(2013011017);山西省研究生创新项目(20143096)
杨昆朋(1988-),男,硕士研究生,主要研究方向为计算机辅助设计与图形学。

