移相全桥ZVS DC-DC变换器的复合控制

江心利，王成宝，于少娟，申书霞

(太原科技大学电子信息工程学院，太原 030024)

移相全桥ZVS DC-DC变换器的复合控制

江心利，王成宝，于少娟，申书霞

(太原科技大学电子信息工程学院，太原 030024)

针对移相全桥ZVS DC-DC变换器抗干扰性差的缺点，研究了基于系统辨识的自校正PID复合控制策略。该策略是在采用极点配置法的基础上，又采用递推最小二乘法对系统的参数进行了辨识和估计，从而使系统达到自适应控制的目的。设计了复合控制策略下的控制器，最后通过MATLAB仿真结果验证了自校正PID复合控制使系统具有良好的动态和稳定特性，尤其是具有较强的抗干扰性，从而验证了方法的合理性。

自校正PID;极点配置;辨识;参数估计

损耗小和工作效率高是移相全桥ZVS DC-DC变换器的优点，所以其在很多场合被应用[1]。在国外，移相全桥ZVS DC-DC变换器的控制方法有多种，大多是研究深度高的复合控制策略，有着很好的控制效果。而国内，其研究大多存在单一性，所以大多数存在输出稳定性差和抗干扰性差的缺点，不能满足一些高标准的场合，针对此问题，本文在传统PID控制的基础上提出了基于系统辨识自校正PID复合控制的策略，在极点配置进行优化的前提下，又引入最小二乘法对系统进行参数估计，使其能在外界产生干扰时对系统进行辨识，再经算法的优化计算给系统合适的PID参数进行控制。最后，通过MATLAB仿真对比可知，此复合控制策略使系统具有了更好的抗干扰性和输出稳定性。

1 变换器的小信号建模

图1是移相全桥ZVS DC-DC变换器的拓扑结构。辅助网络在工作中给滞后桥臂提供了一个电流源[2]，为滞后桥臂功率管的开通提供了更多的能量。

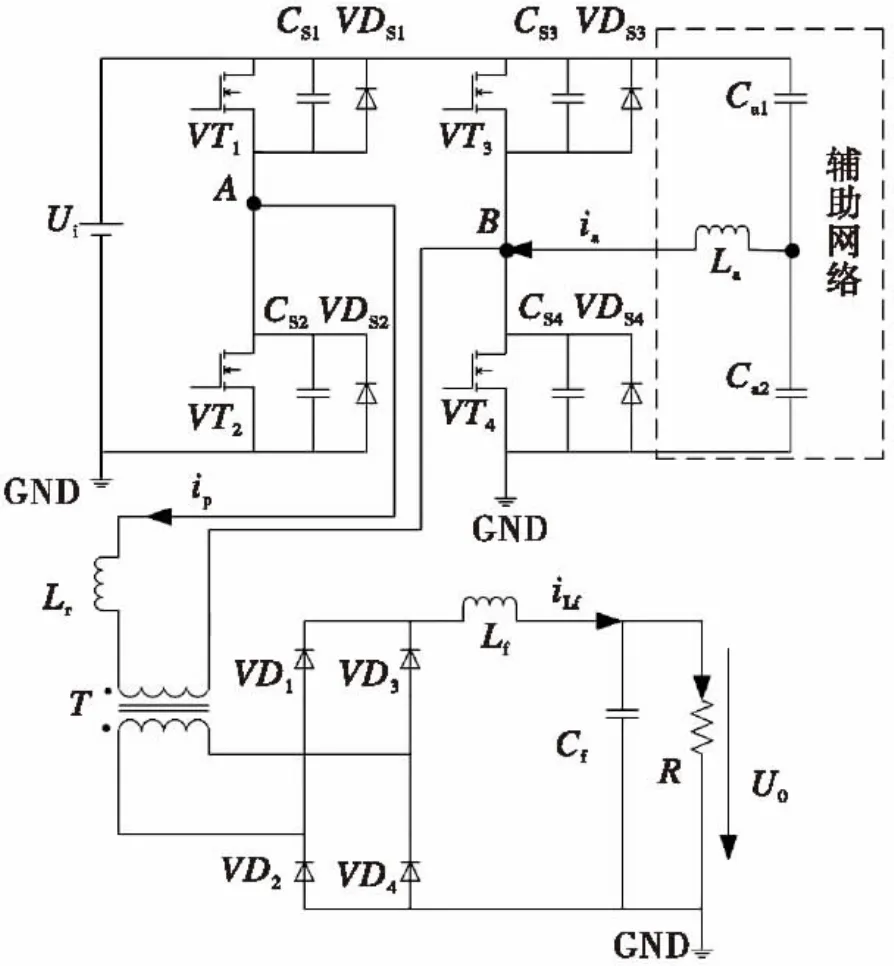
图1 变换器的拓扑结构Fig.1 The topology structure of converter

移相全桥ZVS DC-DC变换器是在Buck电路的基础上衍生而来的[3]，所以此变换器的小信号建模应先以Buck电路为基础进行分析。假设电路中的功率管和二极管都是理想开关，并设开关周期为T，占空比为d，变压器的工作频率为Fs.

功率管的工作状态将Buck电路看作两种模式并加权两种模式下的状态方程可得[4]:

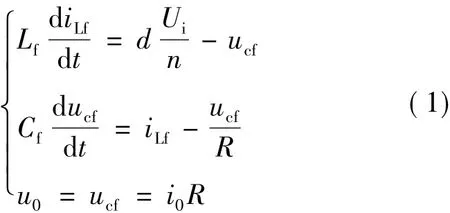
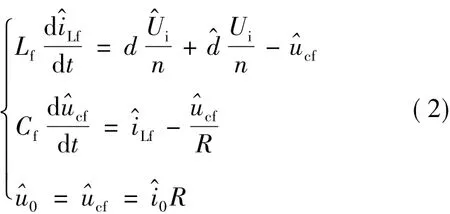
移相全桥ZVS DC-DC变换器的谐振电感Lr和功率管的寄生和外加电容发生谐振能引起占空比的丢失，进而影响变压器副边有效占空比的大小和系统的动态特性[5]。设变压器副边有效占空比为deff，d'为控制信号决定的原边占空比，△d为丢失的占空比，则deff=d'-△d.为建立精确的数学模型需考虑输出滤波电感电流iL的小信号扰动、输入电压ui的小信号扰动和原边占空比d'的小信号扰动对的影响，分别为和d^d，则

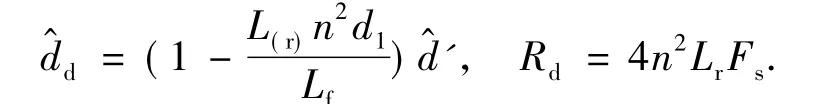
变换器在增设辅助网络后，其小信号等效模型也是在Buck电路模型的基础上建立的，只需令所建模型如图2所示。ZVS DC-DC变换器占空比对输出电压的传递函数Gu0d为[6]:

图2 小信号建模等效电路Fig.2 Small signal equivalent circuit model

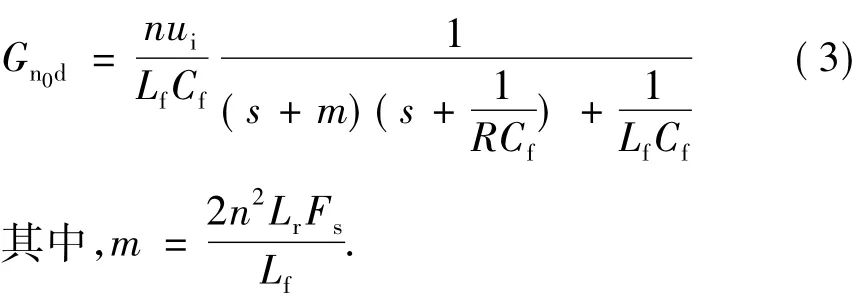
2 自校正PID控制器的设计

自校正PID控制是把辨识出来的参数通过估计递推算法与PID控制算法融合起来而形成的一种能根据外界变化而自动校正控制器参数的一种控制方式，在线辨识可以体现其自校正的能力[7]，其基本控制结构如图3所示。

图3 系统控制的结构框图Fig.3 The structure diagram of system control

其中，d≥1，为纯延迟;ɑ1、ɑ2、b0(b0≠0)、b1为系统待辨识系数。

也可以把式(4)可以写为:

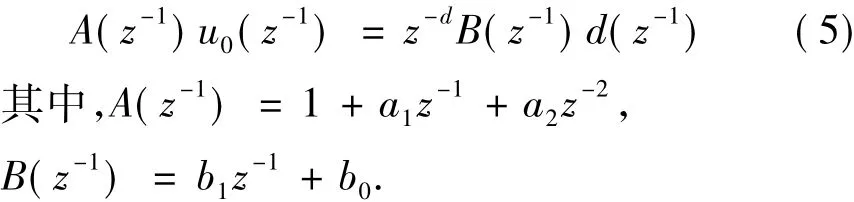
给系统加上扰动C(z-1)ζ(z-1)，并且设C(z-1)= 1+c1z-1+c2z-2+… +Cncz-nc，为避免系统输出端由于突变而引起的振荡，取C(z-1)=1+c1z-1+c2z-2= 1+0.5z-1+0.1z-2，则式(7)可记为:

2.1 增量式PID

由于增量式PID算法运算量小，响应速度快，

由式(3)可知，带辅助网络的ZVS DC-DC变换器是一个二阶系统，且存在非线性特性[8]，为了简化后续过程的计算，可将式(2)进行Z变换为:

且无积分饱和问题[9]，故采用增量式PID，则其简单表示形式为:

其中，u(k)为连续时间PID调节器方程的数字形式;gi(i=0，1，2)为可调参数且与PID的比例、积分和微分系数有关系，u(k)为调节器输出，e(k)调节器输入偏差[7]。

同式(4)相同原理，将式(7)离散化可得:

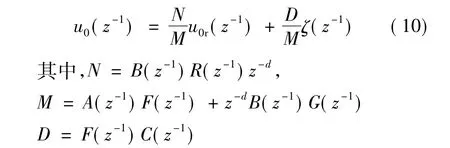
2.2 自校正PID的极点配置

极点配置是通过设计一个反馈控制把闭环传递函数的极点配置在期望的位置。由文献[7]可知，闭环控制系统的结构如图4所示。

为了消除式(6)中ζ(z-1)的常值干扰，调节器必须有积分作用，根据图4可知，此时对应的PID控制表达式为:

其中，G(z-1)=g0+g1z-1+g2z-2，

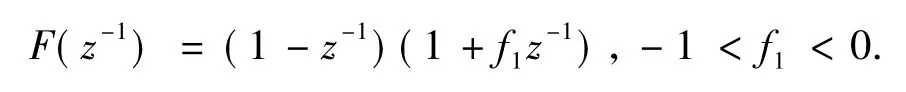
当系统处于稳态且u0(z-1)=u0r(z-1)时，系统才能达到伺服跟踪的效果[10]，此时有 R(z-1) = G(1)=g0+g1+g2，u0r(z-1)为参考输入。

将式(9)带入式(6)得闭环系统输出为:

图4 闭环系统的控制结构Fig.4 The control structure of the closed-loop system

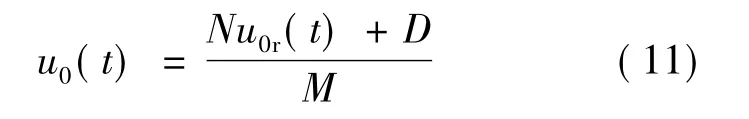
按增广型自校正闭环极点配置的要求可以令期望传递函数分母多项式，即:

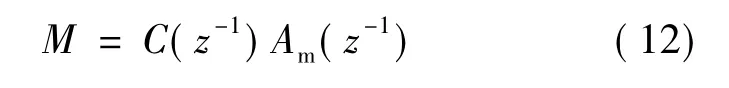
其中，Am(z-1)为期望特征函数多项式。

在对系统进行极点配置时，其配置目标函数通常选择二阶闭环系统的标准形式[11]，其标准形式如式(13):

由图4可知系统闭环方程为:

式(12)的特征多项式的离散形式为:

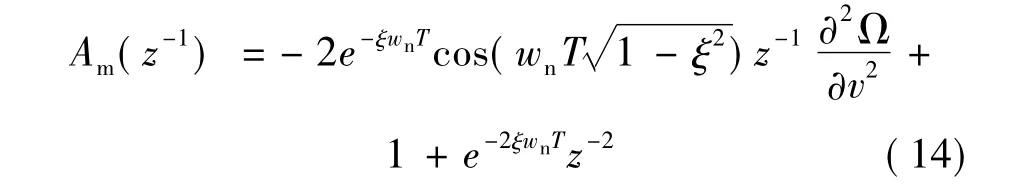
式中，wn为自然振荡角频率(无阻尼)，ξ为系统阻尼比，T为采样周期。

对于式(14)而言，其最佳的稳定状态为阻尼比ξ=0.707，超调量σ%=4.3%(其单位阶跃作用下的)且r(wc)=65.5°(相角稳定裕量)[10];这时，T、wn和ξ存在如下关系:

其中，NT=10～20，考虑实际情况本文取NT= 10，阻尼比ξ=0.7，采样周期T=2 us，带入式(15)计算可得wn=4.44×105rad/s，并将上面数据带入式(14)化简整理可得:

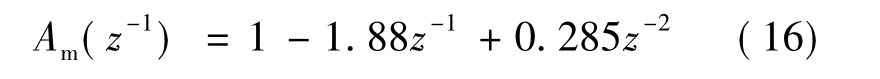
令式(12)两边各项系数对应相等，以此求出g0、g1、g2、f1分别与ɑ1、ɑ2、b0、b2的关系，辨识出系统ɑ1、ɑ2、b0、b2的值就知道PID三个参数的值。

2.3 递推最小二乘法的参数估计

把式(6)改写成下列形式:

进一步化简为:

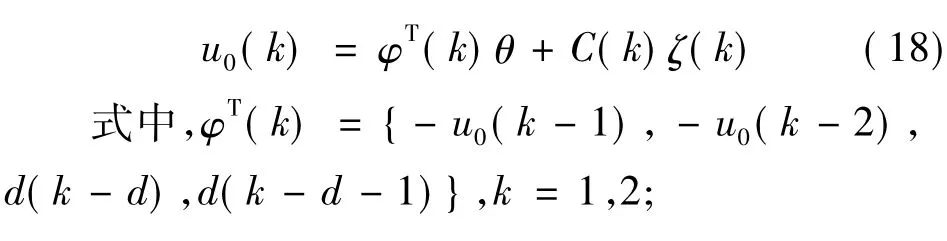
θ=(ɑ1，ɑ2，b0，b1)T.

由于参数估计处理过程中存在数据饱和的问题[12]，所以当增加参数估计时其精确性就会降低。由此在递推参数估计中我们引入了带遗忘因子λ的递推算法，一般λ∈(0.95，0.99)，其形式如下:

2.4 自校正PID控制的流程

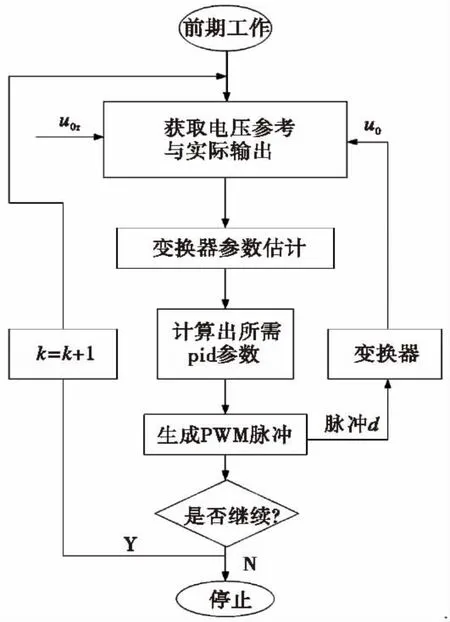
图5 复合控制的流程Fig.5 The process of compound control

由以上分析可以对系统进行自校正PID控制，其控制流程如图5所示。原始参数。图1电路图中各元件参数分别为:La= 4.17×10-5H，Cf=20 uF，Ca1=Ca2=4.87×10-7F，Lr=4.7×10-9H，变比K=0.5，输入电压ui=400 V，把上述参数带入式(3)可得:

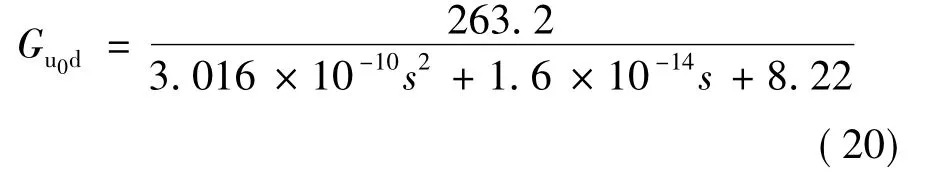
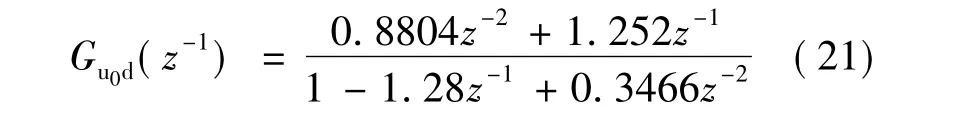
由式(21)可知式(4)中d=1，此ɑ1=-1.28，ɑ2=0.346 6，b0=1.252，b1=0.880 4，带入式(14)可得:f1=0.534，g0=0.316，g1=-0.991，g2=0.243.

根据文献[11]可以把θ的初始值设为，θ= (-1.28，0.3466，1.252，0.8804)，P(0)=108.

3 变换器的仿真结果

将式(20)离散化可得:

3.1 输出电压跟随性及抗负载扰动仿真

在检验变换器输出电压跟随性及抗负载扰动仿真中，使输出参考电压在580 V，550 V和500 V之间变化，并在0.8 s和1.6 s时加重载持续大约0.2 s后恢复，其仿真波形如图6所示。其中(a)图为输入参考电压，(b)图为PID控制下的输出电压，(c)图为自校正PID控制下的输出电压，对比三图可知自校正PID控制不仅使变换器具有良好的跟踪效果，而且抗负载扰动效果也比单纯PID控制效果要好很多，其不到0.2 s就达到稳定500 V，单纯PID控制大约在0.3 s才开始稳定，足见其快速性较好，且没有超调量。

3.2 输入电源扰动仿真

在自校正PID控制与单纯PID控制的抗输入电压扰动仿真中，使输入电压在0.8 s从400 V下降100 V并持续至1.2 s，图7为系统仿真波形，(a)图为输入电压波形，(b)图为单纯PID控制下的变换器的输出电压，(c)为自校正PID控制下变换器输出电压，对比三图可知，自校正PID控制对输入电压的扰动抵抗性较强，在输入电压发生变化时，单纯PID控制下的输出电压有着明显的变化，而自校正PID控制下的输出电压，变化很小，足见其抗干扰性较强，而且自校正PID的响应速度很快，从整体效果来看，其明显优于单纯PID控制，况且单纯PID控制的有超调量。

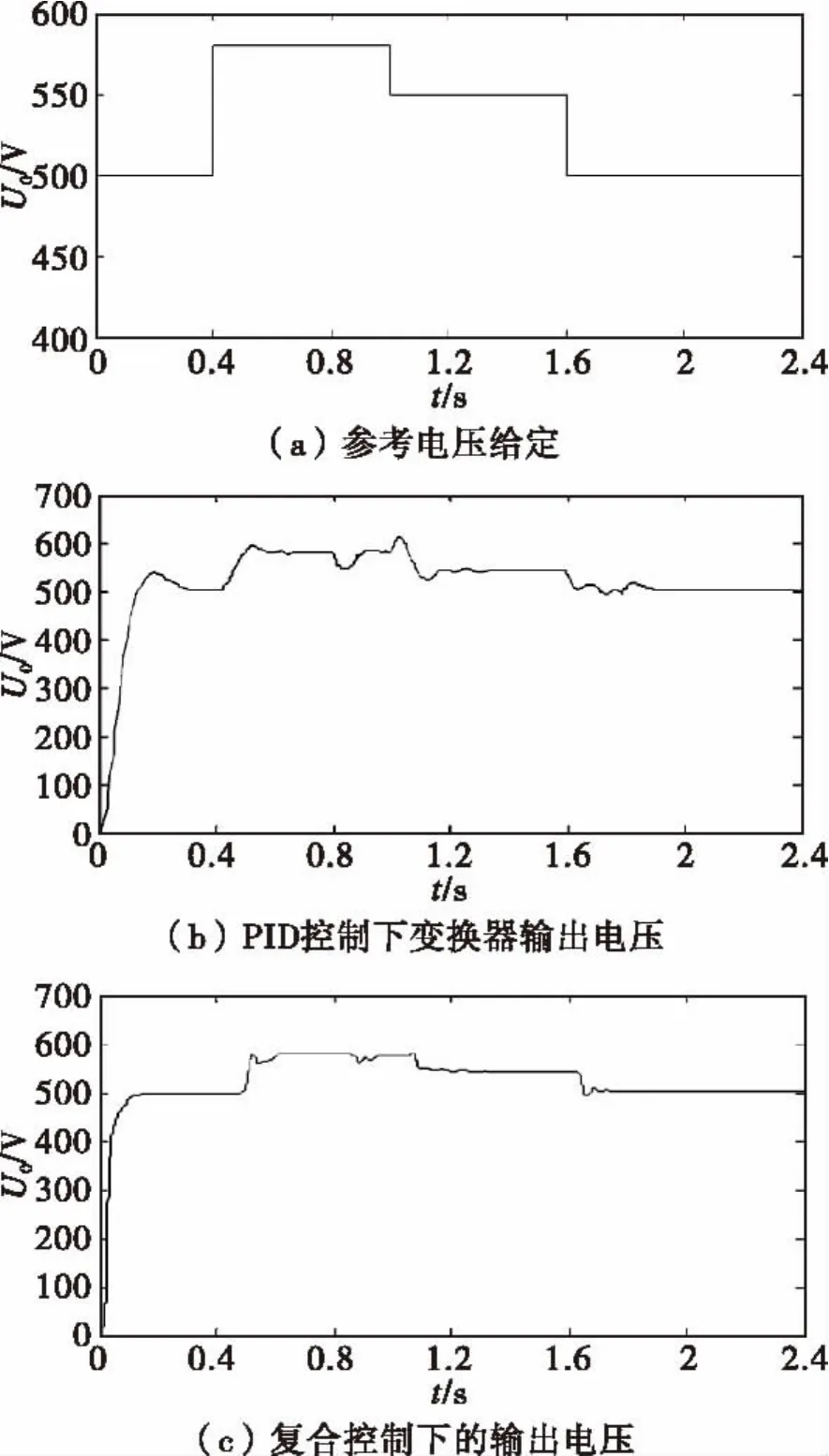
图6 输出电压跟随及负载扰动波形Fig.6 The waveform under the output voltage follower and the load disturbance

3.3 自校正PID控制下的参数辨识

本实验中将系统辨识得到的参数与2.4节中系统建模得到的参数进行对比，由此来验证自校正PID控制器的辨识结果的正确性，图8给出了系统参数辨识的结果。

图8中ɑ1=-1.307 6，ɑ2=0.357 2，b0=1.249 5，b1=0.881 2，而系统建模时的 ɑ1=-1.28，ɑ2= 0.346 6，b0=1.252，b1=0.880 4，把系统辨识得到的参数与建模得到的参数对比可知，虽说存在差异，但是在整体上所得参数具有一致性，这种差异是由于变换器建模的不精确性而造成的[13]。

4 结论

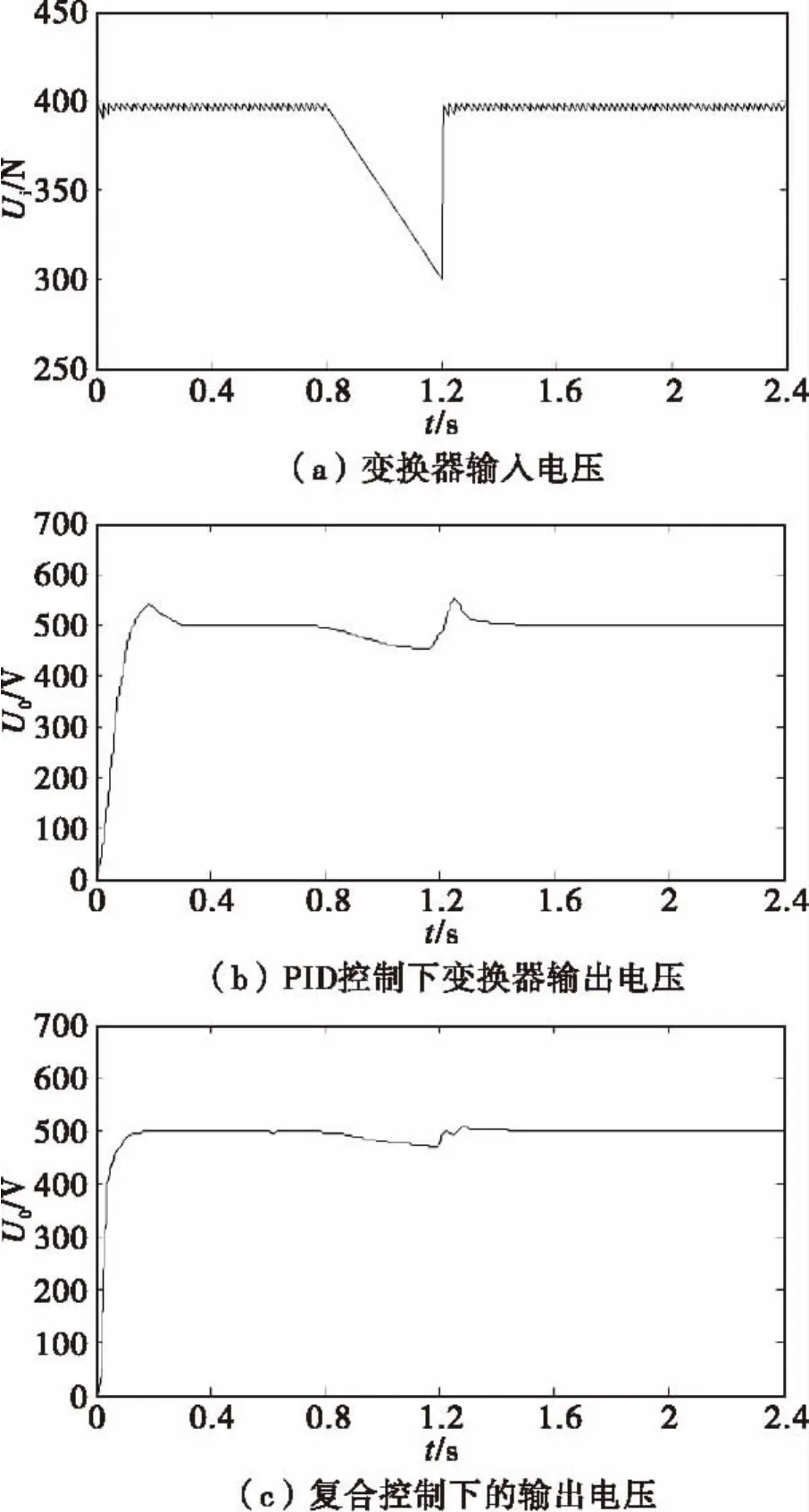
图7 电源输入扰动时的仿真波形Fig.7 Simulation waveform of power input perturbations

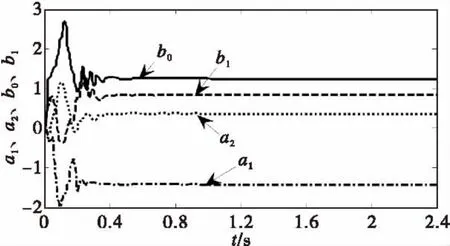
图8 系统参数辨识结果Fig.8 The results of system parameter identification

本文对带辅助网络的变换器采用自校正PID控制设计了其控制器，并通过与传统PID控制下的仿真实验的对比去验证了复合控制的合理性。自校正PID控制不仅具有良好的动态特性，而且抗干扰性明显优于单纯PID控制，其响应速度也比单纯PID控制下的响应速度快。

参考文献:

[1]梁志刚，吴夑华.ZVS-FB变换器辅助谐振网络作用范围研究[J].电力电子技术，2006，40(2):36-39.

[2]徐明，尹斌.一种带辅助支路的移相全桥零电压开关变换器[J].电力电子技术，2006，40(4):56-58.

[3]RAFISHER，KDTNGOA.500KHZ，250WDC/DC converter with multiple output controlled byphase-shifted PWM and magnetic amplifiers[J].Processing of HFPC，2008，24:98-99.

[4]WU CHEN，XIN BO RUAN.A Novel Zero-voltage Switching PWM-Full Bridge Conver ter[J].IEEE Transactions on Power E-lectronics，2008，23(2):793-801.

[5]张沛然，李敏远.一种加辅助网络的移相全桥ZVS PWM变换器[J].电力电子技术，2013，47(2):68-70.

[6]JAROSLAV DUDRIK，NISTOR-DANIEL TRIP.Soft-Switching PS-PWM DC-DC Converter for Full-Load Range Applications[J].IEEE Transactions on industrial Electronics，2010，57(8):2807-2810.

[7]庞中华，崔红.系统辨识与自适应控制MATLAB[M].北京:北京航空航天大学出版社，2009:47-85.

[8]王强，赵志成，桑博.基于改进粒子群算法的分数阶系统辨识方法[J].太原科技大学学报，2014，35(4):202-205.

[9]张兴华，林锦国.基于量子遗传算法的PID控制器参数自整定[J].计算机工程与应用，2007，43(21):218-241.

[10]刘伯春，殷建宁.极点配置自校正PID调节器及其应用[J].过程控制与装置，1994，4:9-10.

[11]SAMUEL J，UNDERWOOD，IQBAL HUSAIN.Online parameter Estimation and Adaptive cont rol of permanent-Magnet Synchronous Machines[J].IEEE Transactions on Industrial Electronics，2010，57(7):2435-2443.

[12]陈振锋，钟彦儒，李洁.嵌入式永磁同步电机自适应在线参数辨识[J].电机与控制学报，2010，14(4):9-13.

[13]AKAO KAWABATA，SHIGENORI HIGASHINO.Parallel Operation of Voltage Source Inver ter[J].IEEE Transactions on Industry，2004，24(2):281-284.

Compound Control for Phase-shifted Full-bridge ZVS DC-DC Converter

JIANG Xin-li，WANG Cheng-bao，YU Shao-juan，SHEN Shu-xia
(School of Electronical and Information Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China)

A self-tuning PID compound control strategy based on system identification is studied to overcome the poor anti-interference of ZVS DC-DC converter.The strategy based on pole placement method is adopted，and the recursive least square method is also used to identify and estimate the parameters for realizing the adaptive control of this system.A controller based on compound control strategy is designed in this study.Finally，the self-tuning PID control is demonstrated to have good dynamic and steady characteristics by the MATLAB simulation，in particular，a strong anti-interference is got as well，thus verifying the rationality of such method.

self-tuning PID，pole placement，identification，parameter estimation

TM46

A

10.3969/j.issn.1673-2057.2015.04.008

1673-2057(2015)04-0278-06

2014-11-11

太原科技大学校博科技研究启动资金(20122033);山西省高校教改项目(J2011130，J2013064);同洲电子科技创新基金(TZ201323);省UIT项目(2014287)

江心利(1987-)，男，硕士研究生，主要研究方向为现代控制理论在电气系统中的应用;通讯作者:于少娟，教授，E-mail:13303413533@189.cn