新型栅元湍流流动及涡结构数值模拟
肖红光,鄢炳火,陈文振
(海军工程大学 核能科学与工程系,湖北 武汉 430033)
新型栅元湍流流动及涡结构数值模拟
肖红光,鄢炳火,陈文振
(海军工程大学 核能科学与工程系,湖北 武汉 430033)
本文利用非稳态雷诺平均模拟(URANS)对非均匀壁厚新型栅元中的准周期性大尺度涡结构和湍流流动特性进行了模拟和分析。结果表明:新型栅元的对流换热能力优于传统栅元的;增加周向角可强化涡结构强度;随周向角的增大,新型栅元摩擦阻力系数呈现先减小、后趋于恒定的变化趋势,而传热系数则会在达到极小值后略有上升。
新型栅元;涡结构;数值模拟;CFD
准周期性大尺度涡结构(简称涡结构)发现于20世纪70年代,至今一直是工程研究中的热点,这种涡结构对棒束流道间的传热和流动特性有重要的影响。
在棒束通道间,涡结构会随P/D(P为棒-棒间距,D为棒直径)的减少而增强[1]。对于类似反应堆内棒直径D较小的栅元,减小P/D会增加制造难度并极易引发机械不稳定性,进而带来流动不稳定威胁[2]。Yan[3-4]指出涡结构的产生与横向涡量梯度有关,而增加横向涡量梯度可通过设置非均匀壁面粗糙度和非均匀壁厚两种方法实现。本文对具有非均匀壁厚的新型栅元内的流动和传热特性进行研究,并分析棒束间的流场分布特征和流动传热变化规律。
1 计算模型
本文所分析的栅元形状为无定位格架的三角形排列棒束(棒束可为实心加热棒,也可为空心传热管),计算域如图1阴影区所示。计算域沿流动方向长度L=600mm,约为涡结构平均实验波长的4倍[5],D=140mm,P/D=1.12。本文以非均匀壁厚周向角θ为分析对象,研究不同θ对新型栅元内流动特性及传热特性的影响,图中θ和α之和为30°,ΔR与间隙区宽度δ的比值为50%,其中,δ=(P-D)/2。计算参数列于表1。分析介质与文献[5]相同,均为空气。

图1 新型栅元示意图Fig.1 Sketch of new lattice
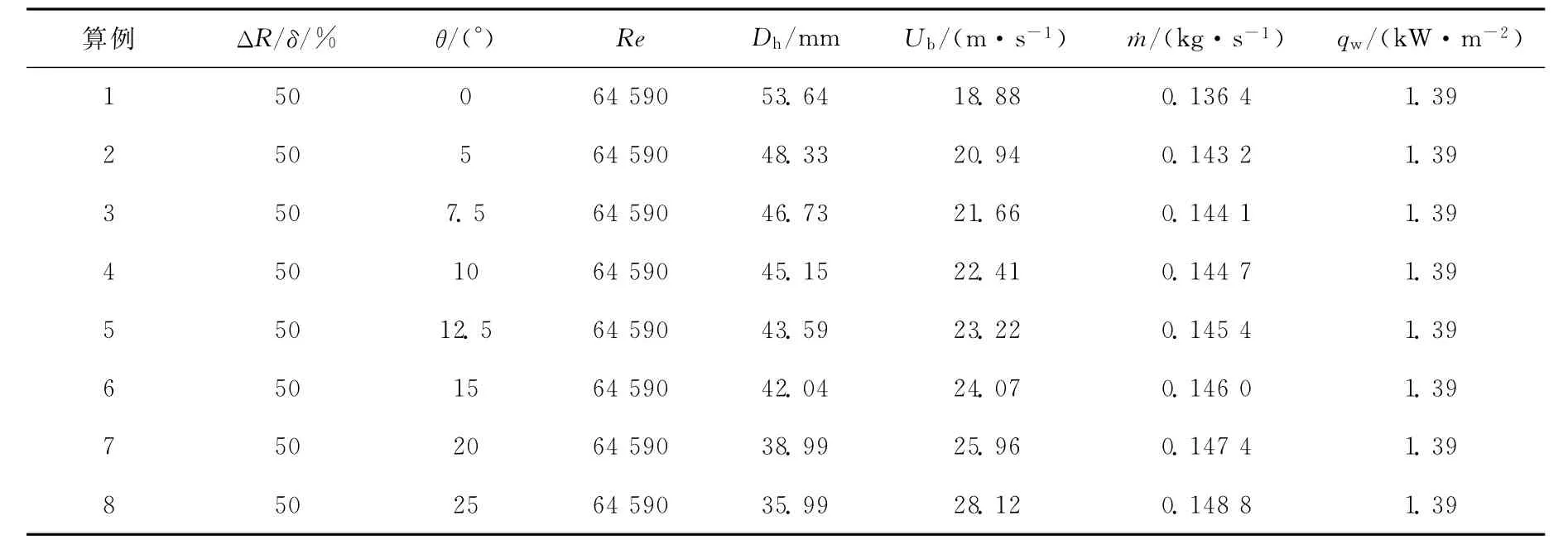
表1 数值模拟主要参数Table 1 Main parameters of numerical simulation
与直接数值模拟(DNS)和大涡模拟(LES)相比,非稳态雷诺平均模拟(URANS)不仅能对涡结构和流场分布特征进行准确模拟,且所需的计算资源不高[6],因而本文选用URANS方法对新型栅元进行分析。
计算采用六面体结构化网格,经网格敏感性分析后,所生成网格数为496 800。在壁面区域,采用低雷诺数模型,第1层网格的y+不超过1.0。设置边界条件时,壁面设定为具有恒热流密度的无滑移壁面,同时设置3对周期性边界条件,分别为进、出口边界1-1和对角位子通道侧面边界2-2、3-3,如图2所示[3],图中阴影部分代表加厚壁面。在数值计算中湍流模型采用雷诺应力模型(RSM),RSM是直接对Reynolds方程中的湍流脉动应力建立微分方程式并求解,其相对于其他两方程模型采用了各向异性的湍流黏度来计算湍流应力,且该模型方程中定义了压力应变项Ф,对于湍流流动结构与湍动能分配具有重要影响,模型能很好地对周期性波动的涡结构进行模拟[7]。压力和速度耦合采用PISO算法,采用二阶迎风格式以提高空间离散控制方程计算精度,计算步长为3×10-5s。

图2 周期性边界条件Fig.2 Periodic boundary condition
2 结果与讨论
2.1 涡结构
目前,Q因子被普遍用于描述和分析涡结构,它包含涡旋和应变两方面特性[8]。本文也用Q因子(图3)来分析新型栅元中的涡结构,其表达式为:

式中:Ωij为反对称项(旋转张量);Sij为1个对称项(应变张量率)。它们可表示为:

图3b~d中,两条虚线内阴影区域表示正Q因子区,即涡旋超过应变的区域,它不受壁面剪应力的影响,从而可从高应变活动区区分出涡旋运动[3]。图3表明,利用数值模拟方法并不能准确预测P/D=1.12、θ=0°的传统栅元中存在的涡结构,但引入非均匀壁厚壁面后,数值模拟结果十分明确地表明了新型栅元中涡结构的存在,且该结构随θ的增大逐渐增强。

图3 Q因子Fig.3 Qfactor

图4 间隙区中心处的横向波动速度Fig.4 Transverse oscillation velocity in center of gap region
图4为相同时间间隔内间隙区中心线中点处无量纲横向波动速度(沿x方向)曲线。由图4a可看出,数值模拟方法得到θ=0°的传统栅元的横向波动速度振幅基本为0,即未发现存在子通道间较大规模的横向流动交混。图4b~d表明,在引入非均匀壁厚壁面后,横向波动速度不仅具备了较大的振幅,且曲线呈现明显的周期性,表明涡结构的产生会引起相邻子通道间横向流动交混。该结构频率随θ的增大而逐渐增大,但波动速度幅值却基本保持在8%~10%主流速范围内,说明θ的改变主要影响涡结构的频率特性,无量纲频率参数Strouhal数定义为:St=fDh/ub(4)式中,f为频率。图4b~d所示的3种情况下St分别为0.24、0.20和0.18。
由图1可知,当ΔR/δ=50%、θ=25°时,新型栅元几何形状更接近于P/D=1.06的稠密栅元,而Krauss等[5]的实验结果表明,P/D=1.06稠密栅元中涡结构的St为0.15,与本文计算结果较接近。
2.2 轴向速度

图5 时均无量纲轴向速度等高线图Fig.5 Isocontour of time-averaged dimensionless axial velocity
Krauss等[5]的实验表明,当P/D=1.12时,在对数律层速度u沿径向的分布遵循u+=2.5ln y++4.5。Horváth等[9]指出,当Re>40 000时,该对数分布表达式为u+=(1/κ′)ln y++5.5,且与P/D无关,其中,κ′=0.4,为von Karman常数。本文计算发现,对于具有非均匀壁厚的新型栅元,u+沿径向的对数分布能很好地与经验公式相吻合,但在对数律层,本文u+数值模拟结果较Krauss等[5]实验值高15%,较Horváth等[9]数值模拟结果高10%,如图6所示,图中实线为Krauss等[5]对数律层实验值,点线为黏性底层经验公式,虚线为Krauss等[5]实验值±15%区间。u提取位置为流道最宽处,即沿壁面周向角φ=0°处。

图6 轴向速度对数分布Fig.6 Logarithmic plot distribution of axial velocity
2.3 壁面剪应力
图7示出了归一化的壁面剪应力分布。在加厚壁面区和非加厚壁面区的交界处壁面剪应力分布会出现振荡,当θ较小时,壁面剪应力分布与P/D=1.12通道的实验数据吻合较好,但随θ的增大,壁面剪应力分布与P/D=1.06通道的实验数据更接近,说明增大θ的作用与减小P/D的作用在一定程度上类似。摩擦阻力系数λ可表示为:
式中:Cf为壁面摩擦系数;为时均壁面剪应力;ρ为流体密度。
表2列出了传热与摩擦阻力系数,可发现,在θ较小时,摩擦阻力系数随θ的增大而逐渐减小,在θ超过15°后趋于恒定。

图7 壁面剪应力Fig.7 Wall shear stress
2.4 温度

表2 传热与摩擦阻力系数Table 2 Coefficients of heat transfer and frictional resistance
新型栅元中的Nu表达式为:

式中,κ为流体热导率。

图8 时均无量纲温度等高线图Fig.8 Isocontour of time-averaged dimensionless temperature
各算例Nu随θ的变化(表2)与摩擦阻力系数的变化趋势相同,在θ较小时,Nu随θ的增大而逐渐减小,在θ超过15°后Nu有所提高,其原因可能与当θ=15°时流场不均匀程度最大有关。Webb[10]提出1个评价参数K,用于判定换热器设计时沿程阻力和Nu的综合影响,其表达式为:

式中,Nu0和λ0分别为均匀壁面情况下的Nu和λ值。
由表2可知,算例中K均大于1,说明新型栅元可在不增加泵损耗的条件下增强换热能力,即新型栅元结构优于传统栅元结构。K会在θ=15°时出现一极小值,在工程应用中可通过权衡能耗和传热的重要性选择θ。
3 结论
本文利用URANS方法成功模拟出具有局部加厚壁面新型栅元内的涡结构,并对周向角对涡结构和流场的影响进行了分析,得出以下结论:
1)θ的改变主要影响横向波动速度频率,且通过Q因子分析可知,θ的增大确实强化了涡结构。
2)θ的改变极大地影响了速度场和温度场的分布,速度场和温度场分布随θ的增大经历了由相对均匀到不均匀,再重新到相对均匀状态的过程。
3)随θ的增大,摩擦阻力系数λ和Nu均会先单调降低,但λ会在θ超过15°后趋于恒定,而Nu则会略有上升,这与流场和温度场的变化趋势有关。
4)新型栅元结构优于传统栅元结构,在新型栅元设计时须权衡能耗和传热两方面的影响。
[1] NINOKATA H,MERZARI E,KHAKIM A.Analysis of low Reynolds number turbulent flow phenomena in nuclear fuel pin subassemblies of tight lattice configuration[J].Nuclear Engineering and Design,2009,239(5):855-866.
[2] 陈文振,于雷,郝建立.核动力装置热工水力[M].北京:中国原子能出版社,2013:153-160.
[3] YAN B H.Periodic large scale vortex structure in rectangular channels with non-uniform wall roughness[J].Nuclear Engineering and Design,2011,241(8):2 948-2 955.
[4] YAN B H.A new lattice with enhanced heat transfer characteristics[J].Nuclear Engineering and Design,2013,265(12):254-261.
[5] KRAUSS T,MEYER L.Experimental investigation of turbulent transport of momentum and energy in a heated rod bundle[J].Nuclear Engineering and Design,1998,180(3):185-206.
[6] CHANG D,TAVOULARIS S.Numerical simulations of developing flow and vortex street in a rectangular channel with a cylindrical core[J].Nuclear Engineering and Design,2012,243:176-199.
[7] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004:132-137.
[8] HUNT J,WRAY A,MOIN P.Eddies,stream,and convergence zones in turbulent flows,CTRS88[R].Stanford:Centre for Turbulence Research,1988.
[9] HORVÁTHÁ,DRESSEL B.Numerical simulations of square arrayed rod bundles[J].Nuclear Engineering and Design,2012,247:168-182.
[10]WEBB R L.Performance evolution criteria for use of enhanced heat exchanger surfaces in heat exchanger design[J].International Journal of Heat Mass Transfer,1981,24(4):715-726.
Numerical Simulation of Turbulent Flow and Vortex Structure in New Lattice
XIAO Hong-guang,YAN Bing-huo,CHEN Wen-zhen
(Department of Nuclear Energy Science and Engineering,Naval University of Engineering,Wuhan 430033,China)
The quasi-periodic large scale vortex structure and turbulent flow characteristic in a new lattice with non-uniform wall thickness was investigated with the unsteady Reynolds-averaged Navier-Stokes(URANS)method.It is revealed that the new lattice is more superior to the traditional lattice.The increase of spanwise angle can enhance the vortex structure intensity.The resistance coefficient decreases firstly and then becomes stable with the increase of spanwise angle.But the heat transfer coefficient increases slightly after reaching minimum.
new lattice;vortex structure;numerical simulation;CFD
TL33
:A
:1000-6931(2015)05-0842-06
10.7538/yzk.2015.49.05.0842
2014-01-18;
2014-04-01
国家自然科学基金资助项目(51206183)
肖红光(1987—),男,山东聊城人,博士研究生,从事反应堆安全分析和热工水力研究

