基于液压变压器蓄能器变刚度机构的液压激振方法

吕云嵩

(南京工程学院机械工程学院，南京211167)

基于液压变压器蓄能器变刚度机构的液压激振方法

吕云嵩

(南京工程学院机械工程学院，南京211167)

提出了一种新的激振方法，即用液压变压器与蓄能器、作动缸组成变刚度弹性机构，该机构连接振体构成液压激振振动回路。调节变压器的排量可以改变弹性机构的刚度，进而改变振动回路的固有频率和振动特性。由于这种方法不再依赖液压阀控制振动，所以能够避免节流损失。构建了激振回路数学模型，进行了仿真分析，表明该回路的固有频率可通过液压变压器在一定范围内任意调节。

液压激振;液压变压器;节能

液压激振具有低频特性好，推力大，容易实现过载保护，环境适应性强等优点，因而在低频大功率振动台和工程机械等领域得到广泛应用［1］。液压激振的一个主要缺点是工作能效低。长期以来，液压激振回路一直沿用两种主流结构，一种是用配流阀控制作动缸的结构，另一种是用电液伺服阀控制作动缸的结构。前者主要用于工程机械及施工机具，后者多用于液压振动台等实验设备。由于这两种结构都是利用液压阀的阻尼效应控制振动的，故其理论能效最高只有37%。目前，学术界对液压激振技术的研究主要集中在如何提高振动控制精度、增加输出功率以及拓展频宽等方面［2－7］，而有关节能方面的研究则鲜有报道。液压变压器是一种传动比能无级调节的液压动力偶合装置［8－9］，是近年来业界研究的一个热点。本文提出的液压激振方式的基本构想是:利用液压变压器与蓄能器组成变刚度机构，再用该弹性机构与作动缸组成液压激振回路，通过调节变压器的排量可以改变激振回路的固有频率，进而控制回路的振动特性。由于这种方法不再依赖液压阀控制振动，所以能够避免由此产生的阻尼损失。

1 系统工作原理简介

如图1，液压油缸活塞杆与振体固连，液压缸油缸的油口与液压变压器的初级油口连接，变压器的次级油口对称连接两只皮囊式蓄能器。皮囊式蓄能器是弹性(容性)元件，其工作压力随变压器转角dφ变化

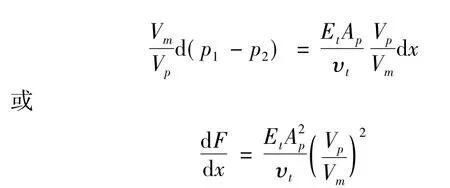
上式为油缸的刚度表达式，其值它可以通过变压器的排量Vp/Vm调节。

式中，d F为油缸位移增量，Et为蓄能器油－气综合体积弹性模量，υt为蓄能器油－气总容积，Ap为活塞面积，Vp为变压器次级排量，Vm为变压器初级排量。

振体处于中位时油缸两腔压力p1=p2，两蓄能器压力p3=p4。当振体偏离中位时，两只蓄能器之间产生压差pL2=p3－p4，压差pL2对变压器形成阻力矩并使其初级产生压差pL1=p1－p2。压差pL1对振体产生复位力，该力随振体位置偏移量的增大而增大。振体经液压缸－变压器与蓄能器构成了一个振荡回路。改变变压器的排量可以改变其初、次级压差比pL1/pL2，即改变了弹性机构刚度，于是振荡回路的频率特性也随之改变。图1振体左侧为外部干扰xi和干扰系统等效弹簧，它可以是一个普通液压激振系统。

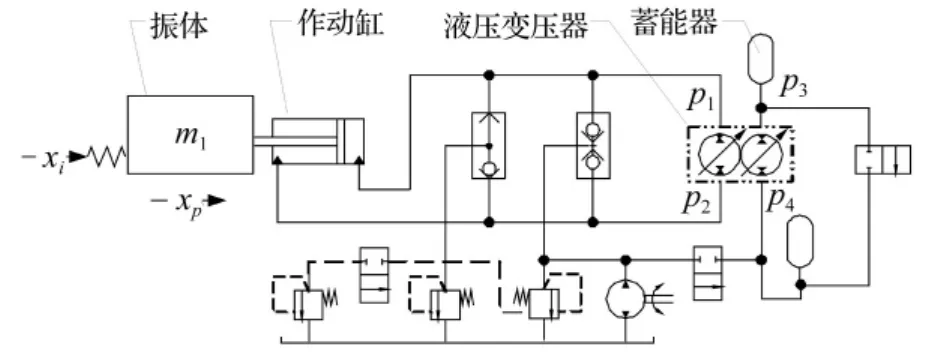
图1 液压变频激振回路原理图Fig.1 Schematic of hydraulic variable frequency vibration circuit

2 回路基本方程

变压器受压力受油缸两腔压力p1、p2和两个蓄能器压力p3、p4的作用产生转矩，其中p3、p4与变压器转角的关系取决于皮囊式蓄能器压缩气体p－v的变化规律。激振系统工作时，蓄能器气体状态的变化更接近绝热过程，但为了简化数学推导将其视为等温过程。

2.1 变压器力平衡方程

式中:ε为变压器角加速度，J为液压变压器转动惯量，Vm为变压器初级排量，Vp为变压器的次级排量，ηm为变压器机械效率，pg为皮囊式蓄能器充气压力，vg为蓄能器容积，N为液压变压器转过的圈数，ηv为液压马达容积效率，Ap为活塞有效面积，xp为振体位移。

2.2 液压回路连续性方程

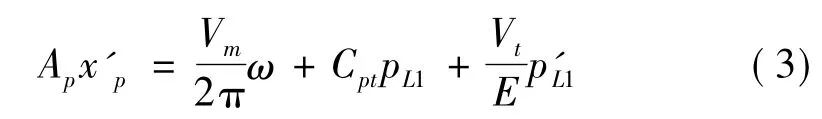
式中:ω为液压变压器转动角速度，Cpt为泄漏系数，Vt为系统总容积，E为系统综合体积弹性模量。

2.3 振体力平衡方程式中:xi为输入位移。

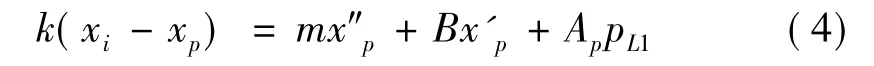
2.4 回路微分方程

联立式(1)～式(4)，消去中间变量ω和pL1，得系统受迫振动微分方程

式中:ωkm为振体与干扰系统等效弹簧的固有频率，ωEm为振体与液压系统的固有频率，ωEJ为变压器与液压系统的固有频率，η为系统总效率，ξ为阻尼比。

在没有外界输入即xi=0的情况下，式(5)可以写成

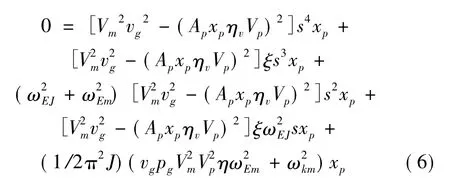
式(6)是自由衰减振动微分方程，s为拉氏算子。上式中各项的系数是活塞位移xp的函数，说明回路的动态特性对振幅有依赖性。为了便于分析，该方程可以用分段法分解为若干个常系数微分方程［10］。各段微分方程除了系数不同，其结构形式是完全一样的，故只需考察其中一段就可以定性地了解系统的动力学特性。

3 回路分段微分方程及频率特性

为了得到常系数微分方程，须将蓄能器的p－v关系在xp=0处做线性化处理。为简便起见，设蓄能气体状态按等温规律变化，则

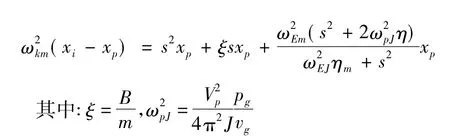
ωpJ为变压器与蓄能器的固有频率。νg为蓄能器气体体积，pg为蓄能器充气压力。对于无外界输入干扰即xi=0的自由振动，上式的特征方程为:

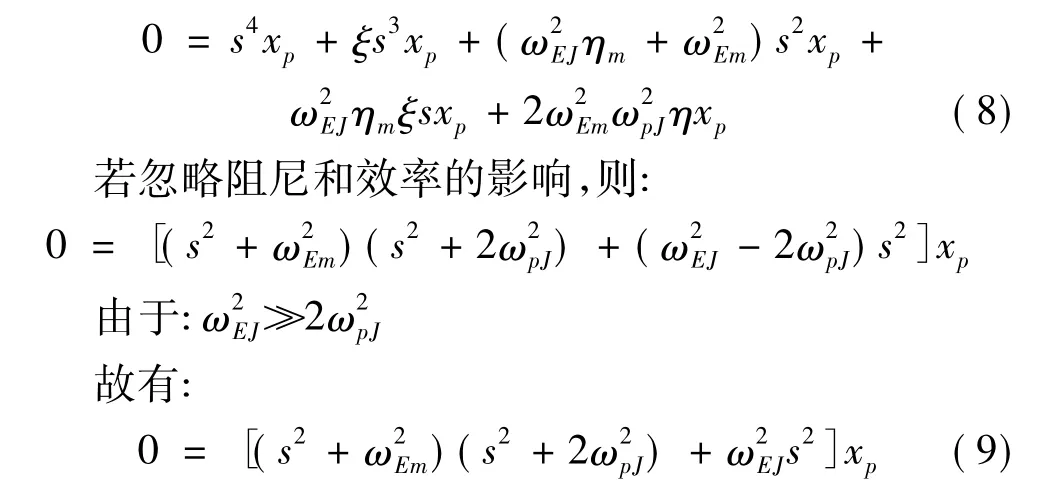
式(9)表明，该激振回路主要由振体－液压系统，变压器－蓄能器两个二阶振荡环节串联而成，其固有频率分别为ωEm和ωpJ。当回路结构参数确定以后ωEm就是固定参数。ωpJ与蓄能器工作压力即与振体的工作点有关，且与变压器次级排量Vp成正比。在振动过程中，当排量Vp值一定时，ωpJ值是脉动变化的，脉动频率就等于固有频率ωpJ。独立二阶项系数ωEJ是变压器液压振荡环节的固有频率，ωEJ与变压器初级排量Vm成正比。二阶项对回路频率特性的影响随ωEJ的增加而增加。

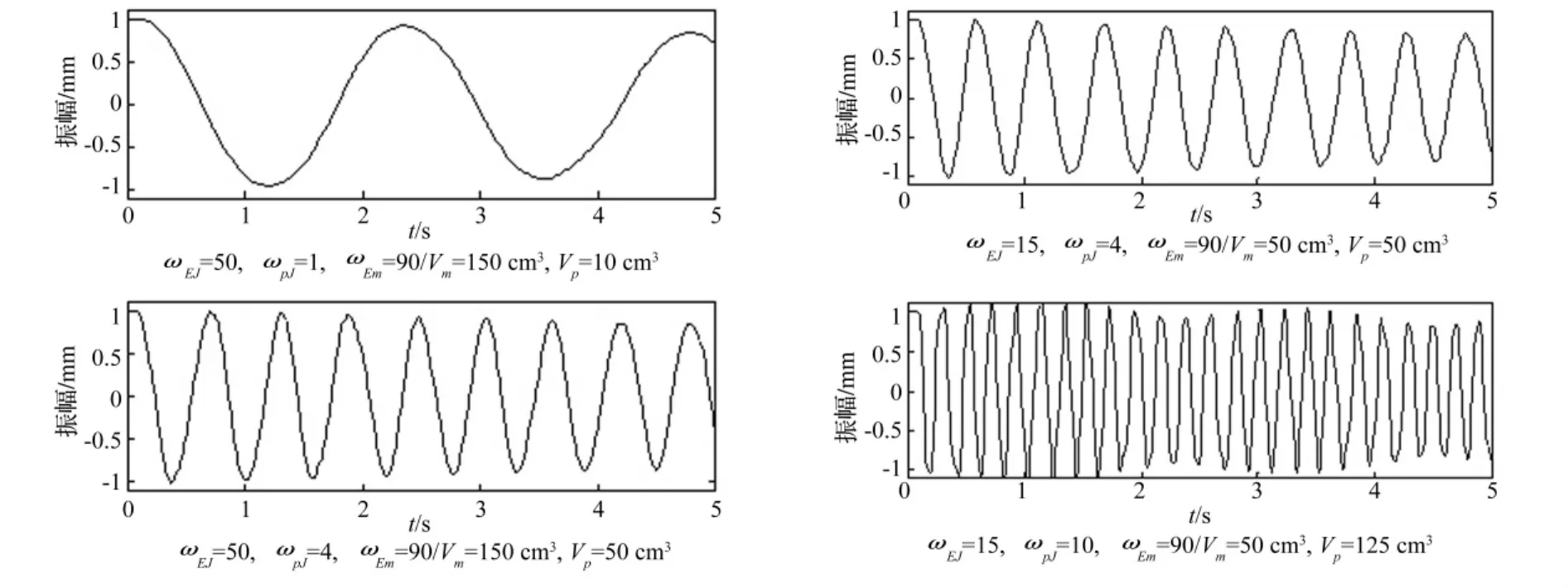
图2 式(9)的数值解Fig.2 Numerical solution of equation No.9

通常ωEm≫ωpJ，ωEJ≫ωpJ，故回路的频率特性由基频ωpJ主导。设式(9)的初值为［1 0 0 0］，可以算出其数值解，代表性数值解曲线见图2。由图2可知，式(9)的振动频率与ωpJ正相关，与ωEJ则负相关，但ωEJ的影响程度远小于ωpJ。因为ωEJ与ωpJ分别与变压器初、次级排量Vm和Vp成正比，故回路的频率特性可通过Vm和Vp在一定范围内任意调节。

4 数值仿真

以上结合激振回路的物理结构，概要地分析了激振回路的频率特性，下面利用数字仿真对回路的动力学特性做进一步分析。利用回路基本方程式(2)～式(4)可以写出回路状态方程。

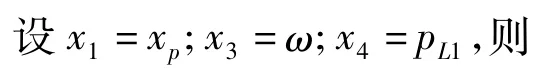
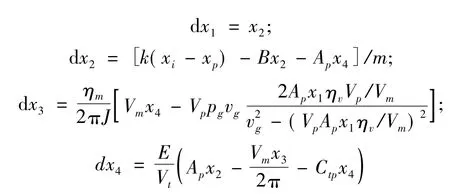
激振回路主要结构数据(见表1)。

表1 激振回路参数表Tab.1 Parameters of vibration circuit

假定仿真初始条件为:振体位移xp=10 mm，振体运动速度x'p=0，变压器转速ω=0，变压器初级压差pL1=0。图3～图6为不同变压器初、次级排量下的代表性仿真曲线。

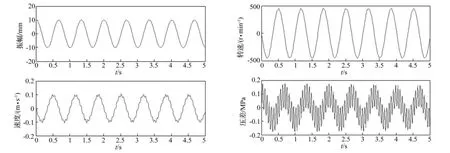
图3 变压器初、次级排量Vm=150 cm3，Vp=10 cm3Fig.3 Primary and secondary displacement of hydro－transformer:Vm=150 cm3，Vp=10 cm3

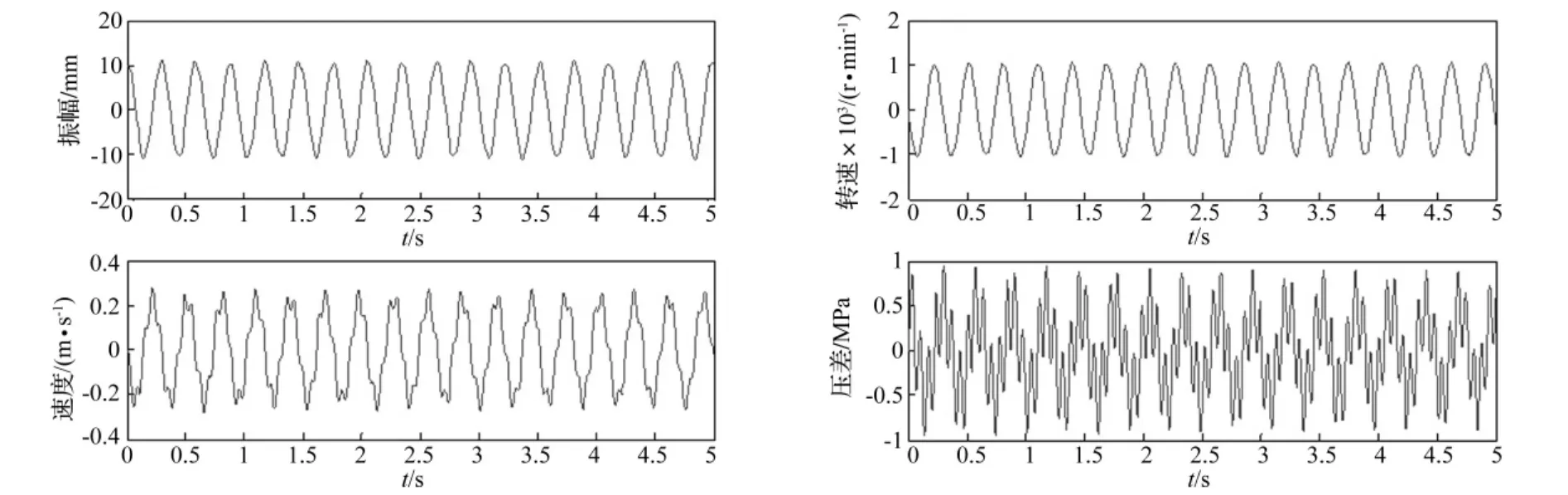
图4 变压器初、次级排量Vm=150 cm3，Vp=50 cm3Fig.4 Primary and secondary displacement of hydro－transformer:Vm=150 cm3，Vp=50 cm3

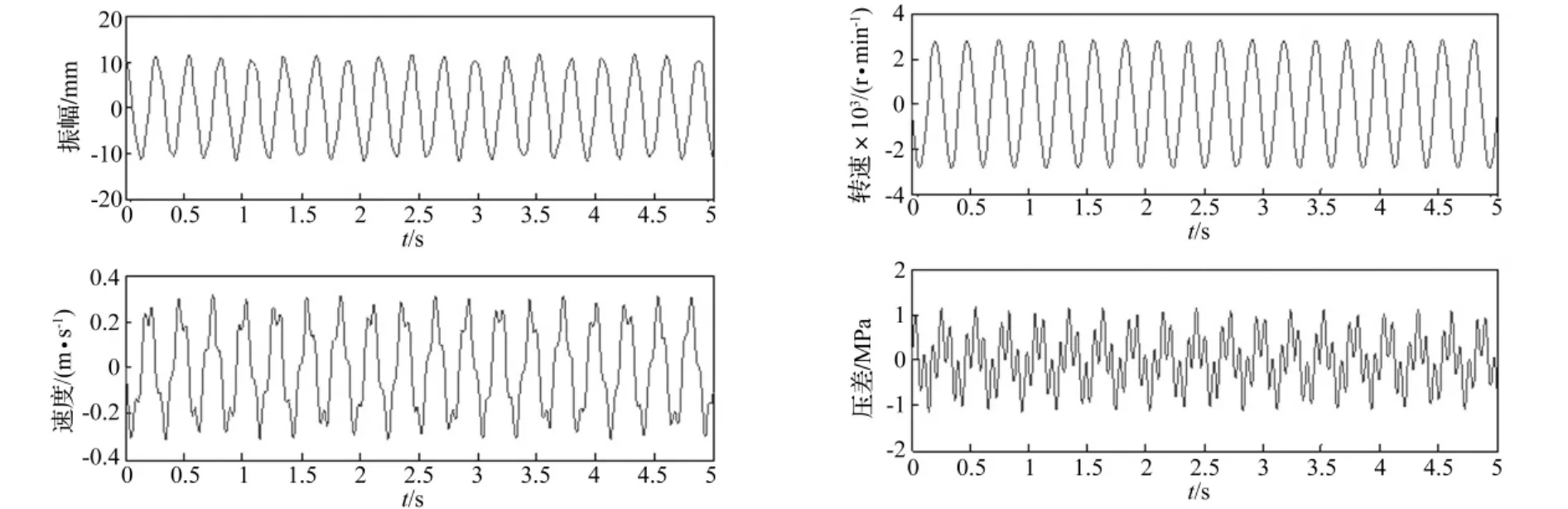
图5 变压器初、次级排量Vm=50 cm3，Vp=50 cm3Fig.5 Primary and secondary displacement of hydro－transformer:Vm=50 cm3，Vp=50 cm3

图6 变压器初、次级排量Vm=50 cm3，Vp=125 cm3Fig.6 Primary and secondary displacement of hydro－transformer:Vm=50 cm3，Vp=125 cm3

每组图的左上图为振体振幅xp，左下图为振体运动速度x'p，右上图为变压器转速ω，右下图为压差pL1。将上述各图与图2比较不难发现，两组振幅曲线的频率随激振回路中二阶环节固有频率ωEJ和ωpJ的变化趋势是一致的，即随比值ωpJ/ωEJ的增大而增大。对于相同的ωEJ和ωpJ，状态方程算出的振体振动频率要高于分段方程(9)算出的频率，两者间的误差是分段方程所做简化引起的。因振体质量较大，故固有频率ωEm对其振动频率的影响可以忽略。ωEm的影响主要体现在液压系统中的高频压力脉动，它会抬高系统压力峰值，且容易引起振动和噪音。由图可见，高频压力波的振幅会随比值ωpJ/ωEm的增大而减小。ωEm的另一种影响是当振体改变运动方向时会引起速度波动。

5 结论

(1)以液压变压器－蓄能器和作动缸及振体组成的激振回路，振体的自然振动频率可以根据需要通过变压器的排量来调节，避免了阀控缸型液压激振方法必须依赖阀的节流作用调节振动参数，故而节能。

(2)激振回路是由两个串联的二阶振荡环节和一个独立二阶项组成的。振体的自然振动频率主要取决于频率较低的变压器－蓄能器二阶振荡环节的固有频率ωpJ，ωpJ与变压器的次级排量Vp成正比。独立二阶项系数ωEJ是变压器－液压缸的固有频率，它与变压器的初级排量Vm成正比，振体的自然振动频率随ωEJ增大而减小。振体－液压缸构成固有频率为ωEm的高频振荡环节，其影响主要体现在回路压力波动上。

［1］邢彤，左强，杨永帅，等.液压激振技术的研究进展［J］.中国机械工程，2012，23(3):362－367.

XING Tong，ZUO Qiang，YANG Yong－shuai，et al.Progresses of research on hydraulic vibration technology［J］.China Mechanical Engineering，2012，23(3):362－367.

［2］Yang Z D，Huang Q T，Han JW，et al.Adaptive inverse control of random vibration based on the filtered－X LMS algorithm［J］.Earthquake Engineering and Engineering Vibration，2010，9:141－146.

［3］Tagawa Y，Kajiwara K.Controller development for the EDefense shaking table［J］.Proceedings of the Institution of Mechanical Engineers，Part I:Journal of Systems and Control Engineering，2007，22:171－181.

［4］栾强利，陈章位，贺惠农，等.三级阀控液压振动台控制策略研究［J］.振动与冲击，2014，33(24):138－143.

LUAN Qiang－li，CHEN Zhang－wei，HE Hui－nong，et al.Control strategy for a hydraulic shaker controlled with a 3－stage electro－hydraulic servo valve［J］.Journal of Vibration and Shock，2014，33(24):138－143.

［5］李小彭，赵光辉，梁亚敏，等.旋转阀式液压振动沉拔桩机实验系统特性分析［J］.振动与冲击，2014，33(21):90－95.LI Xiao－peng，ZHAO Guang－hui，LIANG Ya－min，et al.

Characteristics of a test system for a hydraulic vibratory piling machine with a rotary valve［J］.Journal of Vibration and Shock，2014，33(21):90－95.

［6］邱法维，沙锋强，王刚，等.地震模拟振动台控制技术及软件研究［J］.液压与气动，2011(6):98－101.

QIU Fa－wei，SHA Feng－qiang，WANG Gang，et al.Shaking table control technology and software research［J］.Chinese Hydraulics＆Pneumatics，2011(6):98－101.

［7］阮健，李胜，裴翔，等.2D阀控电液激振器［J］.机械工程学报，2009，45(11):125－132.

RUAN Jian，LI Sheng，PEI Xiang，et al.Electrohvdraulic vibration exciter controlled by 2D valve［J］.Journal of Mechanical Engineering，2009，45(11):125－132.

［8］徐兵，马吉恩，杨华勇.液压变压器瞬时流量特性分析［J］.机械工程学报，2007，43(11):44－49.

XU Bing，MA Ji－en，YANG Hua－yong，et al.Analysis of instantaneous flow rate character of hydraulic transformer［J］.Journal of Mechanical Engineering，2007，43(11):44－49.

［9］张树忠，邓斌，柯坚.基于液压变压器的挖掘机动臂势能再生系统［J］.中国机械工程，2010，21(10):1161－1166.

ZHANG Shu－zhong，DENG Bin，KE Jian，et al.Research on energy regeneration system of hydraulic excavator's boom based on hydraulic transformer［J］.China Mechanical Engineering，2010，21(10):1161－1166.

［10］李宪奎，吴晓明，方一鸣，等.构造结晶器非正弦振动波形函数的方法［J］.机械工程学报，2000，36(1):67－70.

LIXian－kui，WU Xiao－ming，FANG Yi－ming，et al.Method to construct waviness function of mold non－inusoi dal oscillation［J］.Journal of Mechanical Engineering，2000，36 (1):67－70.

Hydro-vibration method based on variable-stiffness elasticmechanism consisting of hydro-transformer and accumulator

LÜYun－song
(School of Mechanical Engineering，Nanjing Institute of Technology，Nanjing 211167，China)

A new method about hydro－vibration was put forward.The hydro－vibration circuit was equipped with a variable－stiffness elasticmechanism that consists of a hydro－transformer，an accumulator and an actuator.The stiffness of the mechanism could be changed by adjusting the displacement of the transformer，thereby changing the natural frequency and the vibration characteristics of the circuit.Since vibration wasn't controlled by hydro－valve，the throttle loss of energy could be avoided.Math－modeling and digital simulation of the system was done showing that natural frequency of the system could be adjusted in a wide bandwidth bymodulating the displacement of the transformer.

hydraulic vibration;hydraulic transformer;variable stiffness elastic mechanism;energy conversation

TH113.1

A

10.13465/j.cnki.jvs.2015.23.032

江苏省自然科学基金项目(BK2012866)

2015－06－29修改稿收到日期:2015－09－10

吕云嵩男，教授，1957年生