锥顶钢储罐内部可燃气体爆炸冲击荷载的CFD模拟

胡 可，赵 阳，王 震，2

（1．浙江大学空间结构研究中心，杭州 310058；2．浙江省建筑设计研究院，杭州 310006）

锥顶钢储罐内部可燃气体爆炸冲击荷载的CFD模拟

胡 可1，赵 阳1，王 震1，2

（1．浙江大学空间结构研究中心，杭州 310058；2．浙江省建筑设计研究院，杭州 310006）

钢储罐常用于液化天然气、石油等易燃易爆物的储存，一旦起火爆炸，短时间内将产生极大的爆炸冲击波，造成储罐严重破坏并带来灾难性后果。爆炸冲击荷载的合理确定是钢储罐爆炸破坏分析与安全设计的重要基础。利用计算流体动力学FLUENT软件，基于k－ε湍流模型和EDC燃烧模型，建立了能够模拟储罐内部爆炸流场变化情况的CFD模型，获得了特定位置处的超压时程，与TNT当量模型相比其模拟结果更接近罐内可燃气体爆炸的实际情况。进一步考察了储罐高径比、可燃气体浓度与种类以及初始压力等因素对爆炸冲击荷载的影响。研究表明：储罐高径比越大、罐内初始压力越大、可燃气体活性越高、越接近化学计量比浓度时，气体燃烧反应速度越快，爆炸冲击荷载越大。

钢储罐；可燃气体；爆炸冲击荷载；超压；CFD

钢储罐内储存的液化天然气、石油等物资属于易燃易爆物，在其生产、储存与使用过程中容易出现火灾与爆炸事故。为确保储罐结构类工程的安全，需对其进行爆炸动力响应分析和抗爆性能评价。爆炸冲击荷载的合理确定是钢储罐爆炸破坏分析与安全设计的重要基础。

容器内爆炸冲击荷载的主要研究方法包括实验模拟和数值模拟。通过实验模拟可获得特定位置的超压时程曲线及爆炸冲击波特性，无疑是最直接、可靠的方法。然而，对容器内部爆炸流场进行实验模拟耗资较大，周期较长，实测数据有限，难以完整反映爆炸流场的变化情况。相比实验方法，通过数值模拟可获得容器内壁面各处冲击荷载时程的完整信息，能够更好地研究容器内部爆炸流场的分布特征和规律。TNT当量法是一种简单实用的方法，它利用目前已较为完备的TNT爆炸实验数据及模型参数，通过爆热能、超压峰值或冲量等效转化为TNT当量模型后进行数值模拟［1］。近年来，随着计算流体力学及流固耦合理论的发展，基于场仿真模型的数值模拟技术已成为可燃气体爆炸过程研究的重要手段。对于大型储罐中的可燃气云爆炸这类蒸气云爆炸，可直接采用已有的气体爆炸数值模型进行计算流体动力学（CFD）数值模拟［2－3］。目前，关于受限空间可燃气体爆炸的数值模拟，国外学者已进行了一系列的研究工作，如文献［4］利用火焰轨迹方法对密闭管道内可燃气体混合物爆炸过程进行了数值模拟，文献［5］对爆炸管中气体爆炸火焰传播进行了数值模拟。此外，国际上已开发了一些能有效模拟气体爆炸的动力学软件，如AutoReaGas，BLAST，FLACS，FLUENT等，可以较为准确地模拟受限空间气体爆炸过程。国内学者利用这些软件对受限空间气体爆炸过程进行了数值模拟研究，如李小东［6］利用AutoReaGas研究了障碍物和瓦斯浓度对管道中瓦斯爆炸超压场的影响，蒋军成［7］利用FLUENT对连通容器内气体爆炸流场进行了数值模拟，孙金华［8］通过FLUENT模拟了20 L近球形密闭罐内可燃气体爆炸后火焰的传播过程。

目前，可燃气体爆炸的数值模拟大多针对管道或小型密闭容器，对于大型钢储罐内部爆炸冲击荷载的研究还十分有限。本文首先利用计算流体动力学软件FLUENT对小型圆柱型容器内甲烷／空气预混气体的爆炸过程进行了CFD模拟，并将模拟结果与实验结果进行对比分析，验证了该CFD方法模拟此类密闭容器内气体爆炸的有效性与准确性。然后，利用此方法对大型钢储罐内部可燃气体爆炸过程进行模拟，并考察储罐高径比、可燃气体浓度与种类以及罐内初始压力等不同因素对内部爆炸冲击荷载的影响。

1 理论模型与实验验证

1.1 基本控制方程

密闭空间可燃气体爆炸过程是一个快速的燃烧反应过程，满足质量守恒、动量守恒、能量守恒和化学组分平衡方程，各控制方程的通用形式见式（1）［9］。

式中：ρ为密度，t为时间，u为速度矢量，φ为通用变量，Γ为广义扩散系数，S为广义源项；式中各项依次为瞬态项、对流项、扩散项和源项。对于特定的方程φ、Γ、S具有特定的形式，表1给出了三个符号与各特定方程的对应关系。

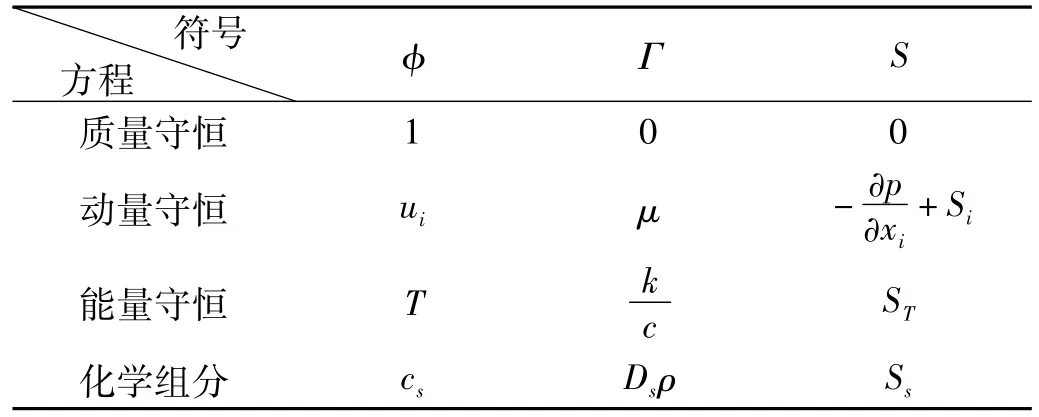
表1 通用控制方程中各符号的具体形式Tab.1 Specific form of symbols in general control equation

表1中，μ为动力粘度，p为流体微元体上的压力，T为温度，k为流体的传热系数，c为比热容，ST为粘性耗散项，cs为组分s的体积浓度，Ds为组分s的扩散系数，Ss为组分s的生产率。

1.2 湍流燃烧模型

式（1）中的各守恒关系可通过三维非稳态的Navier-Stokes方程组进行求解，但运用Navier-Stokes方程对湍流流动进行直接数值计算时，必须采用很小的时间与空间步长才能分辨出湍流中详细的空间结构及变化剧烈的时间特征，而这对内存空间和CPU运行速度的要求非常高，因此直接数值求解目前还无法运用于工程计算。本文利用Reynolds平均法将Navier-Stokes方程组对时间进行平均，引入k－ε湍流模型使方程组封闭。该湍流模型是在关于湍动能k的方程的基础上引入了一个关于湍动耗散率ε的方程而形成的k－ε两方程模型。该模型的计算收敛性和精确性都非常符合工程计算的要求，是在工业应用中被普遍使用的湍流模型。

由于可燃气体燃烧爆炸的化学反应机理比较复杂，为了简化计算可采用单步不可逆反应模型。而气体燃烧反应速率一般可根据四种燃烧模型计算：层流有限速率模型、层流有限速率／涡耗散模型、涡耗散模型和涡耗散概念（Eddy-Dissipation-Concept，EDC）模型。本文选用EDC模型，该模型是涡耗散模型的扩展，能够在湍流流动中考虑详细的化学反应机理。另外，由于密闭容器中气体的燃烧爆炸以及火焰的扩展速度较快，模拟过程不考虑密闭空间与外界的热交换。

1.3 数值方法

FLUENT在算法上主要采用有限体积法，通过求解描述每种组成物质的对流、扩散和反应源的守恒方程来模拟容器内部气体的燃烧或爆炸。对于压力与速度耦合处理，采用半隐方法来求解压力耦合方程的SIMPLE算法。另外，在反应流中获得收敛解比较困难，这是由于爆炸流场流动中伴随的化学反应导致模型中质量、动量和物质运输方程的强烈耦合，本文采用亚松弛方法来处理这类耦合问题。

1.4 实验验证

由于直接对大型钢储罐内可燃气体的爆炸过程进行实验模拟不现实，本文首先对已有文献中的一小型圆柱型容器内甲烷／空气预混气体的爆炸过程进行CFD模拟，并将模拟结果与实验结果进行对比分析，以验证数值模型的有效性与准确性。

图1 试验密闭容器与CFD模型初始温度场Fig．1 Confined vessel in the experiment and initial temperature filed of CFD model

图1（a）为文献［10］中试验所采用的密闭圆柱型容器，容器长490 mm，内径340 mm，容积约40 L；图1（b）为圆柱型容器内部初始温度场。由篇幅所限，实验具体内容可参考文献［10］。图2为容器内甲烷体积分数为9．5%时模拟得到的压力时程曲线与实验所测结果的对比。从图中可以看出，两曲线变化趋势大致相同，尤其在达到峰值压力之前，CFD模拟得到的曲线与实验结果基本一致。但实验所测最大爆炸压力略小于模拟值，并且在峰值出现后实验所得曲线开始下降而模拟压力值保持稳定不变。这是由于CFD模型中绝热假设所引起的，实际爆炸过程中的热量耗散会引起压力值的降低。总的来说，通过比较模拟值与实验结果可知，采用该数值模型可以较为准确地获得密闭容器内部的爆炸压力时程曲线。

2 锥顶罐内可燃气体爆炸的CFD模拟

为了能够描述储罐内部可燃气体爆炸的主要特征并易于求解，对模型做以下假设和简化：① 假设钢储罐内部没有紧密排列的设备和隔板等障碍物，也没有液化天然气或石油等液体；② 点火前钢储罐内部气体为均匀的可燃气体与空气混合物，常温且处于静止状态；③ 可燃气体、燃烧产物以及空气均为理想气体（满足理想气体状态方程）；④ 燃烧气体混合物的比热容随温度变化，满足混合规则；⑤ 可燃气体燃烧爆炸过程属于单步不可逆反应；⑥ 爆炸过程中不考虑储罐内部空间与外界的热交换，罐壁为绝热［11］；⑦ 不考虑储罐壁面与气体流动的流固耦合效应，罐壁作刚性壁面处理，已有研究表明，基于刚性壁面假设的解耦方法在多数情况下可获得精度较高的爆炸流场［12－13］。

以半径R＝10 m，高径比H／R＝1．5，顶盖坡度1／2的锥顶钢储罐为例进行分析。由于圆柱形爆炸容器具有轴对称性，模型采用1／2实体建模。模型分为两部分：（1）为储罐内部流体单元，充满处于爆炸极限浓度内的乙炔／空气预混气体，如图3（a）所示，其中O为爆源位置，A为顶盖中心位置，B为顶盖与罐壁周向连接位置，C为与爆源O齐平的近壁面位置；（2）为罐壁单元，图3（b）为罐壁网格划分图。由于单元的网格划分对计算结果有一定影响，通过比较不同网格间距（0．25～1 m）模型的计算结果，本文选择了计算精度与计算效率都能得以保证的网格划分方式，即在前处理软件GAMBIT中对整个计算域进行四面体／混合（Tet／Hybrid）网格划分，网格间距为0．5 m，网格单元总数为126 474。

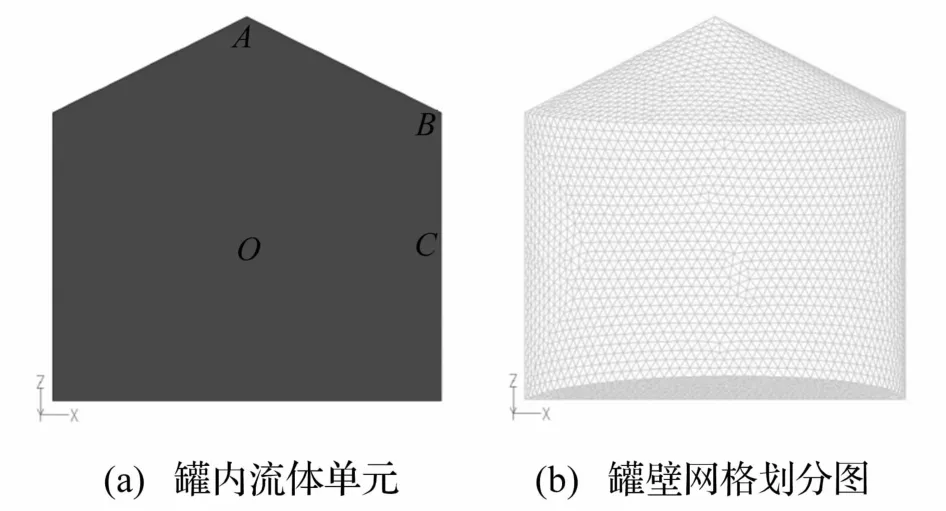
图3 锥顶罐CFD模型Fig．3 CFD model of cone-roof tank

对于储罐内部均匀混合的乙炔／空气，流场初始化条件如下：初始时刻储罐内部温度T（t0）＝300 K，初始压力P（t0）＝0．1 MPa（初始超压为0，即扣除标准大气压），乙炔体积分数为10%；点火时刻，点火区域温度T（t1）＝2 500 K，处于圆柱壳中心位置。

2.1 罐内可燃气体爆炸流场变化情况

表2为不同时刻储罐内部爆炸温度场的变化情况，温度云图中红色区域为高温已燃区，蓝色区域为低温未燃区，红色与蓝色区域之间的黄色区域为反应区（即火焰锋面）。随着时间的推移，火焰锋面以爆源为中心，呈褶皱的球形火焰面向四周扩张，这是因为燃烧反应区是具有一定厚度的区域且处于湍流状态，所以其最前端是弯曲褶皱甚至为已撕裂了的火焰面。当火焰面到达罐壁后，罐内气体已燃烧充分，爆炸冲击波与罐壁发生碰撞反射，反射波折向内部传播；在储罐内部相互碰撞后又折返传向罐壁，发生第二次反射；经过多次反复后，罐内最后达到一个分布较为均匀的爆炸温度场。表3为不同时刻储罐内部爆炸速度场的变化情况，由表3可知，20 ms时罐内爆炸冲击波的速度由0增至145 m／s，40 ms时冲击波以536m／s速度到达罐壁并发生反射，反射波折向储罐内部传播，在储罐内部相互碰撞之后又折返传向罐壁。随着碰撞反射的多次发生，爆炸冲击波的速度也逐渐衰减，80 ms时最大波速为96 m／s，最后达到一个分布较为均匀的爆炸速度场。

表2 储罐内部爆炸温度场的变化Tab.2 Variation of tem perature fields in the tank under internal explosion

表3 储罐内部爆炸速度场的变化Tab.3 Variation of velocity fields in the tank under internal exp losion

2.2 CFD模型与TNT当量模型模拟结果的对比分析

可燃气体的TNT当量WTNT可由式（2）计算［14］：

式中：Wc为蒸气云中参与反应的可燃气体的质量，由本文计算条件可得Wc＝443．1 kg；Qc为可燃气体的燃烧热，对于乙炔取49．85 MJ／kg；QTNT为TNT的爆炸热，可取为4．23 MJ／kg；α为可燃蒸气云爆炸效率因子，对于乙炔取0．19［15］。由此计算可得，WTNT＝992．2 kg。

图4（a）、（b）分别为CFD模型与TNT当量模型模拟得到的储罐内部离爆源O水平距离为2 m、10 m位置处的超压时程曲线，可以看出，两种模型的超压时程曲线均在在第1次反射时达到最大超压峰值，后续波形的超压峰值明显降低；但由于爆源性质的不同，超压时程曲线也存在一定的差异。图4（c）为两种模型模拟得到的从爆源O到罐壁C水平距离的10个等分位置处的最大超压峰值。可以看出，对于TNT当量模型，炸药在点火后瞬间完成爆炸，产生的初始爆炸冲击波速度与超压均为最大，并随着传播距离的增加而迅速衰减；当冲击波到达罐壁时，因壁面反射作用和波的汇聚效应，罐壁附近位置处的超压会有所增大。对于CFD模型，各等分位置处的最大超压峰值变化趋势较为平缓。这是由于可燃气体被点燃后形成的冲击波是随着火焰锋面的发展逐渐加速的，当到达罐壁时爆炸冲击波的速度与超压峰值到达最大；然后经壁面反射折向内部传播并在圆柱壳中心附近区域出现波的汇聚，使得该区域的超压峰值也有所增大。另外，CFD模型在能量方程（见式（1）与表1）中考虑了爆炸过程中的温度效应，因此在爆炸流场处于平稳状态后罐内爆炸压力仍然较高（0．98 MPa左右）；而TNT当量模型未考虑爆炸温度场的变化情况，当爆炸流场处于平稳状态后罐内爆炸压力衰减为初始压力。总体而言，本文采用CFD模型模拟得到的爆炸流场与超压时程与TNT当量模型相比更接近储罐内部可燃气体爆炸的实际情况。

图4 CFD模型与TNT当量模型的模拟结果Fig．4 Simulation results of CFDmodel and TNT equivalentmodel

3 参数分析

影响钢储罐内部爆炸冲击荷载的主要因素有：储罐高径比H／R、可燃气体浓度与种类以及罐内初始压力，下面分别考察这些因素对爆炸冲击荷载的影响。

3.1 高径比的影响

大型钢储罐的高径比H／R一般在0．5～2．0之间，分别取H／R＝0．5，1．0，1．5，2．0进行CFD模拟。储罐内部初始压力为标准大气压0．1 MPa、乙炔体积分数为10%，爆源处于圆柱壳中心位置，考察罐壁附近3个典型位置单元A、B和C（见图3（a））的超压时程，见图5。比较图5中各曲线可知，不同高径比时，各典型位置处的超压－时间曲线变化情况大致相同，均在第1次或第2次反射时达到最大值，后续波形的超压峰值明显降低，且由于尖角约束导致的火焰加速效应，罐内最大反射超压一般出现在顶盖中心区域（A）或者罐壁与罐顶的周向连接处（B）。图6为不同高径比时各典型位置处的最大超压峰值，分析可知，随着高径比的增大，A、B位置处的最大超压峰值均随之增大，这是因为储罐越高，爆源离A、B位置越远，火焰加速时间越长，在火焰锋面到达罐壁时爆炸冲击波的速度越大，从而产生的反射超压就越大。

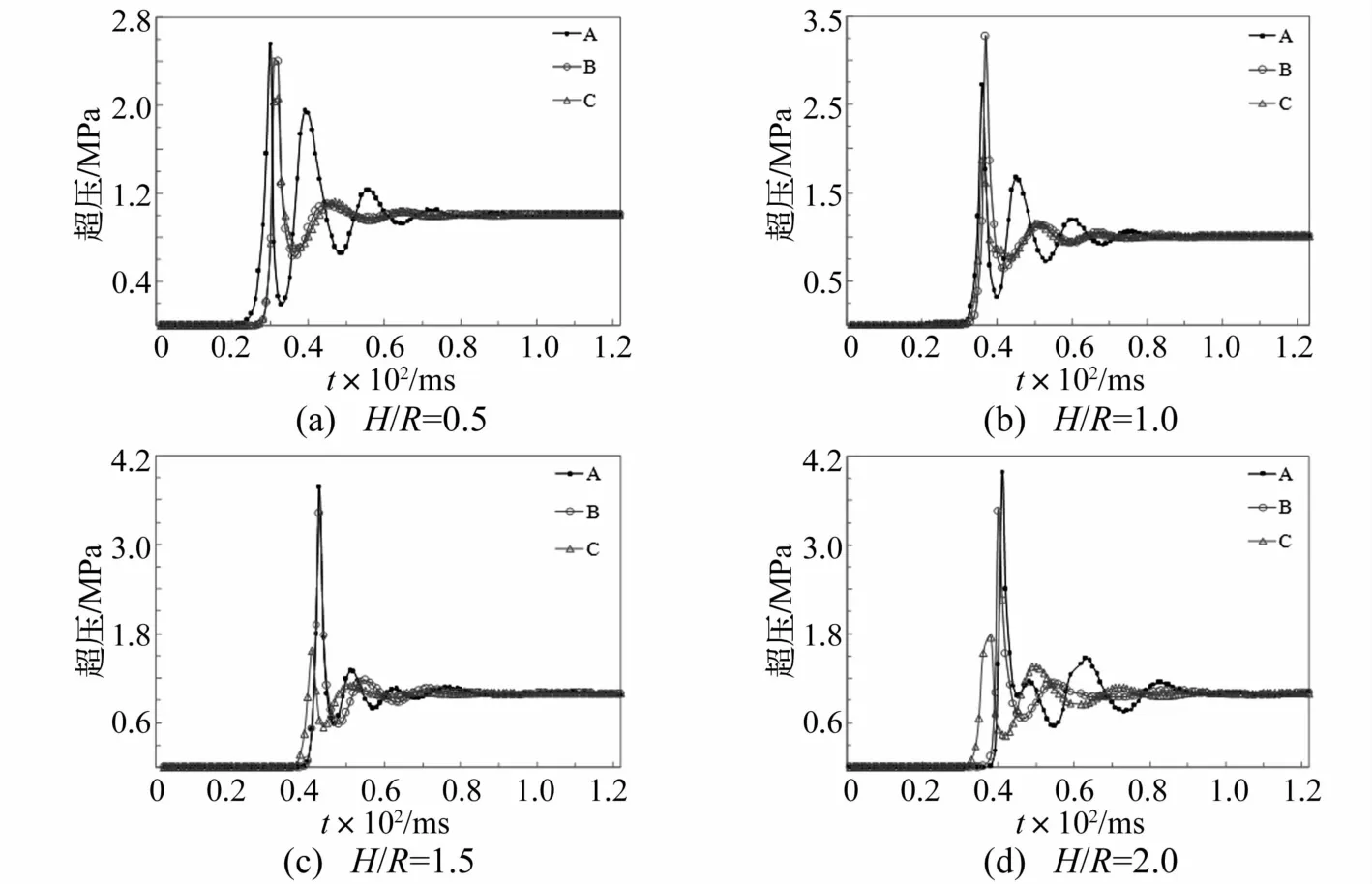
图5 不同高径比时各典型位置处的超压时程曲线Fig．5 Overpressure time history for different values of H／R

3.2 可燃气体浓度的影响

燃料与空气的混合物并非在任何混合比例下都能发生爆炸，而只是在可燃气体浓度合适时，即在爆炸极限之间才能发生爆炸。虽然乙炔在空气中的爆炸极限范围很宽（2．5%～80%），但混合比例不同，燃烧反应速率与爆炸强度也不同。本文对储罐内部不同浓度下的乙炔－空气混合气体的爆炸过程进行CFD模拟，乙炔体积分数分别为5%、8%、10%、15%、20%、30%、40%、50%，储罐高径比H／R＝1．5，内部初始压力为标准大气压0．1MPa，爆源处于圆柱壳中心位置。图7为不同浓度时各典型位置处的最大超压峰值与出现时间。由图7可知，当可燃气体浓度越接近爆炸上、下极限时，气体燃烧反应速率越小，爆炸强度越小；当可燃气体浓度越接近化学计量浓度（对应体积分数为8%）时，气体燃烧反应速率越大，火焰速度越快，壁面反射超压峰值越大。

图6 不同高径比时各典型位置处的最大超压峰值Fig．6 Maximal overpressure peak value for different values of H／R

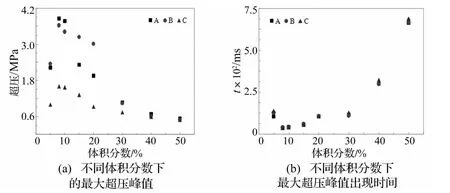
图7 不同浓度时各典型位置处的最大超压峰值与出现时间Fig．7 Maximal overpressure peak value and corresponding time for different values of concentration

3.3 可燃气体种类的影响

储罐内部可燃气体由燃烧发展为爆炸的难易程度以及爆炸后产生的破坏作用在很大程度上取决于气体的性质。气体活性越强，分子扩散越快，则爆炸时产生的爆炸强度就越大，产生爆轰的可能性也越大。文献［16］根据反应活性将气体分为低、中、高三类，见表4。

表4 可燃气体反应活性分类Tab.4 Classification for reactivity of flammable gases

表5 可燃气体的爆炸参数Tab.5 Explosion parameters of flammable gases

本文选取代表高活性气体的乙炔、中活性气体的丙烷以及低活性气体的甲烷作为考察对象，均按照其化学计量比与空气混合，对这三种可燃气体在储罐内的爆炸过程进行CFD模拟，储罐高径比H／R＝1．5，内部初始压力为标准大气压0．1 MPa，爆源处于圆柱壳中心位置。表5为这三种可燃气体在化学计量比与空气混合后的爆炸参数［17］。图8为储罐内充满不同种类的可燃气体时各典型位置处的超压时程曲线。从图中可以看到，乙炔的超压时程曲线十分陡峭，而丙烷和甲烷的超压时程曲线比较平坦且壁面反射超压峰值远小于乙炔。所以，可燃气体活性越高，其燃烧反应速率越大，火焰速度越快，壁面反射超压峰值也越大。

3.4 初始压力的影响

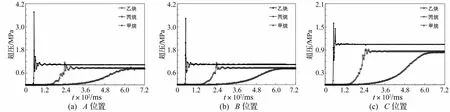
图8 不同种类可燃气体时各典型位置处爆炸超压时程曲线Fig．8 Overpressure time history for different flammable gas

密闭容器内可燃气体发生爆炸时，爆炸压力取决于初始压力、气体摩尔数的变化以及温度的变化。当烃类与空气的混合物发生爆炸时，反应前后气体摩尔数变化很小，爆炸压力主要取决于温度的上升与初始压力的变化。本文分别模拟了初始压力为0．1 MPa、0．2 MPa、0．3 MPa、0．4 MPa时储罐内部可燃气体的爆炸过程，储罐高径比H／R＝1．5，乙炔体积分数为10%，爆源处于圆柱壳中心位置。图9为不同初始压力时各典型位置处的最大超压峰值与出现时间，可见，初始压力越大，气体燃烧反应速率越大，储罐内部爆炸压力越大。

图9 不同初始压力时各典型位置处的最大超压峰值与出现时间Fig．9 Maximal overpressure peak value and corresponding time for different values of initial pressure

4 结 论

采用计算流体动力学数值模拟的方法，利用软件FLUENT建立了CFD模型，实现了储罐内部可燃气体燃烧爆炸过程的模拟，获得以下主要结论：

（1）采用k－ε湍流模型和EDC燃烧模型建立的CFD模型可以较好地模拟罐内爆炸流场的变化情况，能够获得罐壁上任意位置处完整的超压时程曲线。

（2）罐内最大超压值一般出现在罐壁尖角处（如顶盖中心或罐壁－罐顶周向连接处），且在第1次反射超压峰值达到最大。

（3）储罐高径比越大，则火焰加速时间越长，爆炸冲击波到达顶盖或罐壁时的速度越大，壁面反射超压也就越大。

（4）罐内初始压力越大、可燃气体活性越高、浓度越接近化学计量比浓度时，气体燃烧反应速度越快，罐内爆炸压力越大。

［1］Wharton R K，Formby S A，Merrifield R．Airblast TNT equivalence for a range of commercial blasting explosives［J］．Journal of Hazardous Materials，2000，79（1／2）：31－39．

［2］高建丰，杜扬，蒋新生，等．模拟油罐油气混合物爆炸实验与数值仿真研究［J］．后勤工程学院学报，2007，23（1）：79－83．

GAO Jiang-feng，DU Yang，JIANG Xin-sheng，etal．Experimental and numerical investigations of the fuel-airmixture explosion in simulative metal oilcan［J］．Journal of Logistical Engineering University，2007，23（1）：79－83．

［3］Tauseef SM，Rashtchian D，Tasneem A，etal．Amethod for simulation of vapour cloud explosions based on compu-tational fluid dynamics（CFD）［J］．Journal of Loss Prevention in the Process Industries，2011，24：638－647．

［4］Bielert U，Sichel M．Numerical simulation of pre-mixed combustion processes in closed tubes［J］．Combustion and Flame，1998，114（3）：397－419．

［5］Fairweather M，Hargrave G K，Ibrahim SS，et al．Studies of premixed flame propagation in explosion tubes［J］．Combustion and Flame，1999，116（4）：504－518．

［6］李小东，刘庆明，白春华，等．管道中瓦斯爆炸超压场的数值模拟［J］．煤矿安全，2008，39（1）：5－7．

LIXiao-dong，LIU Qing-ming，BAIChun-hua，etal．Numerical simulation of gas explosion overpressure field in tube［J］．Safety in Coal Mines，2008，39（1）：5－7．

［7］王志荣，蒋军成，郑杨艳．连通容器气体爆炸流场的CFD模拟［J］．化工学报，2007，58（4）：854－861．

WANG Zhi-rong，JIANG Jun-cheng，ZHENG Yang-yan．CFD simulation on gas explosion field in linked vessels［J］．Journal of Chemical Industry and Engineering，2007，58（4）：854－861．

［8］王秋红，孙金华，何学超．20L近球形密闭罐内可燃气体流动和火焰传播的数值模拟．南京工业大学学报：自然科学版，2011，33（2）：74－79．

WANG Qiu-hong，SUN Jin-hua，HE Xue-chao．Numerical simulation of combustible gas flow and the flame propagation in 20L nearly spherical and closed tank［J］．Journal of Nanjing University of Technology：Natural Science Edition，2011，33（2）：74－79．

［9］王福军．计算流体动力学分析：CFD软件原理与应用［M］．北京：清华大学出版社，2004．

［10］Kindracki J，Kobiera A，Rarata G，et al．，Influence of ignition position and obstacles on explosion development inmethane-air mixture in closed vessels［J］．Loss Prev．Process Ind，2007，20：551－561．

［11］Fairweather M，Hargrave G K，Ibrahim SS，etal．Studies of premixed flame propagation in explosion tubes［J］．Combustion and Flame，1999，l16（4）：504－518．

［12］Adishchev V V，Kersey V M．Calculation of the shells of explosion chambers［J］．Combustion，Explosion，and Shock Waves，1979，15（6）：108－114．

［13］王震，胡可，赵阳．拱顶钢储罐内部蒸气云爆炸冲击荷载的数值模拟［J］．振动与冲击，2013，32（20）：35－40．

WANG Zhen，HU ke，ZHAO Yang．Numerical simulation of internal vapor cloud explosion loading in dome-roof steel tanks［J］．Journal of Vibration Engineering，2013，32（20）：35－40．

［14］Van Den Berg A C，Lannoy A．Methods for vapor cloud explosion blastmodeling［J］．Journal of Hazardous Materials，1993，34（2）：151－171．

［15］傅智敏，黄金印，臧娜．爆炸冲击波伤害破坏作用定量分析［J］．消防科学与技术，2009，28（6）：390－395．

FU Zhi-min，HUANG Jin-yin，ZANGNa．Quantitative analysis for consequence of explosion shock wave［J］．Fire Science and Technology，2009，28（6）：390－395．

［16］Mercx W PM，Van Den Berg A C．The explosion blast prediction model in the revised CPR14E（yellow book）［J］．Process Safety Progress，1997，16（3）：152－159．

［17］赵衡阳．气体和粉尘的爆炸原理［M］．北京：北京理工大学出版社，1996．

CFD simulation of internal flammable gas exp losion loading in cone-roof steel tanks

HU Ke1，ZHAO Yang1，WANG Zhen1，2
（1．Space Structures Research Center，Zhejiang University，Hangzhou 310058，China；2．Zhejiang Prov．Institute of Architectural Design and Research，Hangzhou 310006，China）

Steel tanks are widely used for the storage of liquefied natural gas，petroleum and other flammable explosive substance．The detonation of these explosives generates high intensity shock wavewithin a short time，which will cause serious damage to storage tanks and bring catastrophic results．A rational evaluation of the explosion loading is the foundation for structure failure analysis and safety designing of tanks．A CFD model was built up based on turbulence model and eddy dissipation concept（EDC）combustion model by use of computational fluid dynamics software Fluent，which can simulate the changes of explosion flow field in tanks and obtain the overpressure time history at typical positions．Compared with TNT equivalentmethod，the result by CFD model is closer to the actual situation of flammable gas explosion in tanks．Furthermore，the influences of height-to-diameter ratio，concentration and species of flammable gas and initial pressure were taken into account．It is shown that，the gas reaction rate and explosion loading enhance along with the increase of height-to-diameter ratio，initial pressure and activity of flammable gas．Moreover，a stoichiometric concentration will also cause a higher explosion pressure and gas reaction rate．

steel tanks；flammable gas；explosion loading；overpressure；computational fluid dynamics（CFD）

TU33；O382

A

10．13465／j．cnki．jvs．2015．12．026

国家自然科学基金项目（51378459）

2013－07－02 修改稿收到日期：2014－05－14

胡可男，博士生，1989年生

赵阳男，博士，教授，1970年生