计入重力弦向分量影响的斜拉索非线性自由振动分析

袁从森，沈锐利，周凌远，李伟东，官 快

（西南交通大学土木工程学院桥梁系，成都 610031）

计入重力弦向分量影响的斜拉索非线性自由振动分析

袁从森，沈锐利，周凌远，李伟东，官 快

（西南交通大学土木工程学院桥梁系，成都 610031）

为了进一步准确计算斜拉索的自振频率，考虑斜拉索的重力在弦向的分量对斜拉索非线性振动的影响，分别建立了斜拉索的垂度微分方程和非线性自由振动方程，采用幂级数法求解垂度微分方程，采用伽辽金法把偏微分方程转化为常微分方程，运用摄动法求得该方程的近似解，并制定了相应的数值计算方法，与理论解进行了比较。研究了考虑索力变化影响后拉索的振动特性，采用了更精确的函数来逼近垂度悬链线，解决了考虑重力在弦向的分量时，用抛物线来逼近垂度悬链线时的精度不足的问题。随着索的长度增加，索的总质量也越来越大，因此要考虑斜拉索的重力弦向的分量对斜拉索的振动的影响。

斜拉桥；斜拉索；非线性振动；弦向分量

Max Irine［1］对索结构的动力理论做了较为详尽的讨论。De SáCaetano［2］对拉索振动理论方法做了较为全面的总结。吴晓［3］建立了斜拉桥拉索大幅振动的非线性动力方程，采用傅里叶级数法研究求解了斜拉索非线性固有振动方程。刘志军［4］研究了斜拉索在平面内的非线性固有振动特性，从考虑抗弯刚度和垂度影响的斜拉索在平面内发生横向振动的非线性自由振动方程出发，对斜拉索发生单模态振动进行了分析。赵跃宇［5］计入斜拉索的抗弯刚度、垂度和几何非线性的影响，利用哈密顿原理建立了斜拉索的非线性振动微分方程。李金海［6］在考虑斜拉索非线性静平衡曲线、抗弯刚度、黏滞阻尼影响的斜拉索平面内非线性振动的基础上，建立了斜拉索非线性运动方程。付英［7］在考虑拉索垂度的情况下建立了深圳湾公路大桥的动力学模型。李寿英［8］推导了覆冰拉索的一阶模态驰振的运动微分方程，并采用龙格－库塔法进行求解，得到了拉索的驰振响应规律。以上学者在研究过程中用二次抛物线代替垂度悬链线，在建立动力微分方程时，没有考虑重力在弦向的分量对斜拉索的振动的影响。周晓东［9］研究了弹性斜拉索内共振非线性特性，在求斜拉索的垂度曲线时，考虑了斜拉索重力在平行于弦向方向上分量的作用；由于该分量的作用，拉索的初始形态不再是关于弦的中垂线对称的、近似抛物线的形状，而是非对称的形态；但是其在建立动力平衡方程时没有考虑斜拉索重力在平行于弦向方向上分量的作用。

一般斜拉桥的拉索在发生大幅横向振动时，应该考虑斜拉索在振动过程中索力的变化，并且考虑非线性项。随着索的长度增加，索的总质量也越来越大，受重力影响，拉索的张力沿弦向变化较大，有必要计入重量弦向分量的影响，更加精确地研究长大斜拉索的非线性振动。

本文假定：只考虑拉索xy平面内的振动，且拉索在x方向的振动很小，可以忽略不计；斜拉索受到的重力沿弦长均匀分布。图1所示为研究对象的坐标体系和结构模型。

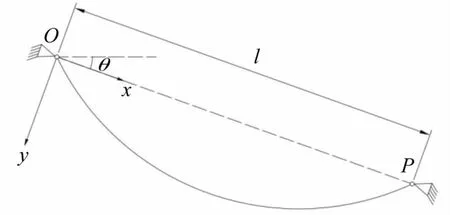
图1 斜拉索示意图Fig．1 The sketch of an inclined cable

由于考虑了重力在弦向的分量，用抛物线来逼近垂度悬链线，精度不够，采用幂级数法求解垂度微分方程，得到更精确的函数来逼近垂度悬链线。

1 斜拉索非线性自由振动微分方程的导出

图1所示的斜拉索，坐标系取弦向op方向为x轴，以垂直于弦向为y轴且以朝下方为正，坐标原点取支撑点O。图中θ和l分别表示斜拉索的倾角和弦长。斜拉索的质量是均匀分布的，单位长度的质量为m，y（x）为拉索静态的垂度函数。在拉索作横向振动时，其弦向拉力增值为S；η（x，t）为拉索横向振动位移函数，其方向沿y轴方向，索的弯曲刚度为EI。

考虑重力在弦向（即为x轴方向）的分量，则拉索的静态弦向拉力将不再是常数，设静态弦向拉力为Sc，其表达式为

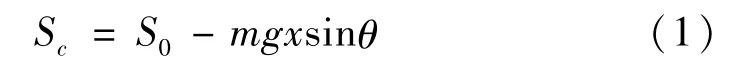
式中：S0为原点O处拉索的静态弦向拉力。

在自重作用下，首先不考虑斜拉索的抗弯刚度，取斜拉索的微段来研究，该微段弧长微分为d s，忽略高阶项，拉索的竖向静力平衡方程为：

式（2）即为垂度微分方程，在此考虑了重力弦向分量的影响。

参照静力平衡方程的推导，斜拉索在平面内作横向振动时，有动力平衡方程：

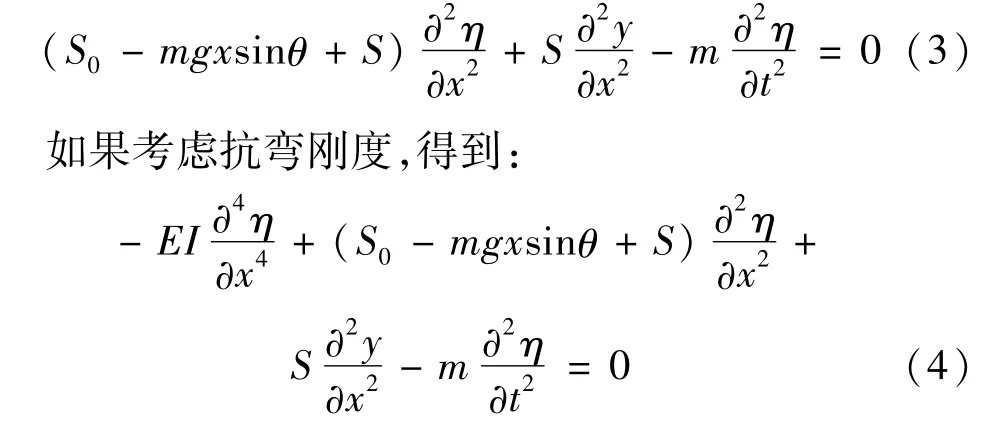
式（4）即为索的动力平衡微分方程。与以前的研究相比，此微分方程考虑了重力在弦向的分量对斜拉索的振动的影响。

变形协调方程为：

或者也可以采用文献［10］的变形协调方程，其本质是一样的。

2 微分方程的近似解析解

2.1 垂度微分方程的求解

我们得到的垂度微分方程式（2）可以采用幂级数法求得近似解：

上式是恒等式，因此方程左端各项的系数全部为零，于是有

2.2 索的动力平衡微分方程的摄动解

假设拉索横向振动位移

把式（5）、式（9）和式（10）代入式（4）中，再利用伽辽金原理，则式（4）就从关于空间的四阶和关于时间的二阶偏微分方程转化为关于时间的二阶常微分方程：

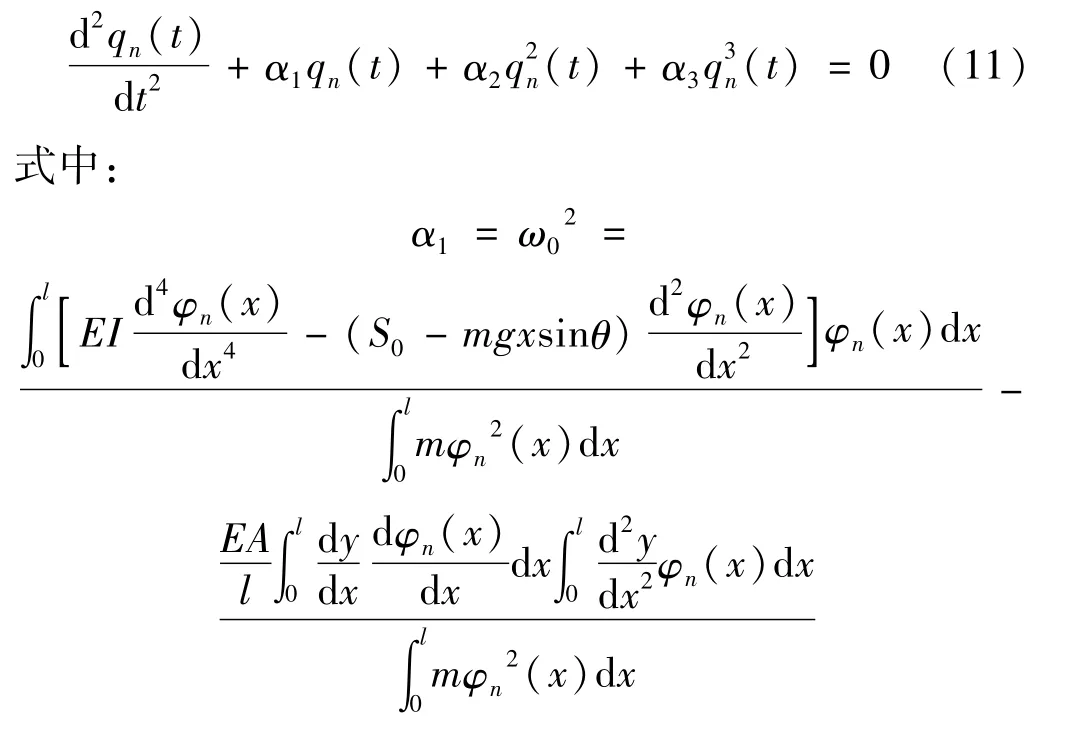
α1为线性影响因素，包括抗弯刚度的影响因素、初拉力（即初始的拉索静态弦向拉力）的影响因素、重力弦向分力影响因素、索力变化和垂度的线性影响因素。其中抗弯刚度的影响因素为：

索力变化和垂度的线性影响因素为：

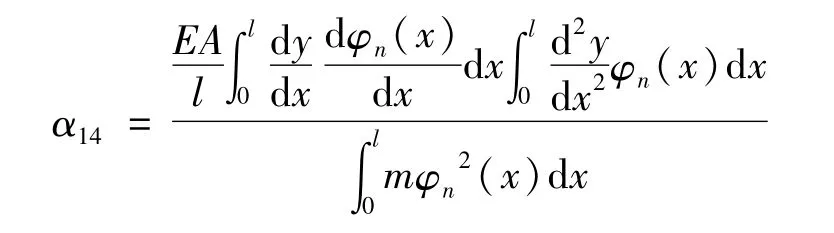
式中：α1＝α11+α12+α13+α14

α2和α3为索力变化和垂度的非线性影响因素：

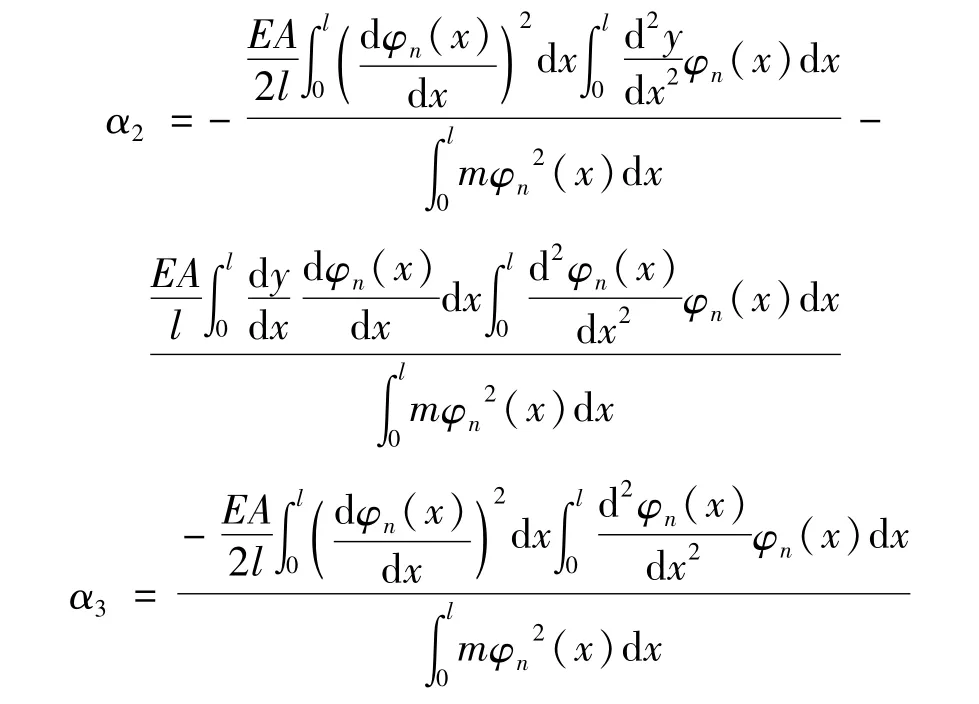
L-P法是一种一致有效的摄动法，我们利用L-P法［11－12］来解式（11）。引进一个无量纲的小参数ε和一个新的自变量τ＝ωt，其中ω为非线性自振频率，是在开始时尚未确定的ε的函数。

假定式（11）的解可以表示成形式为

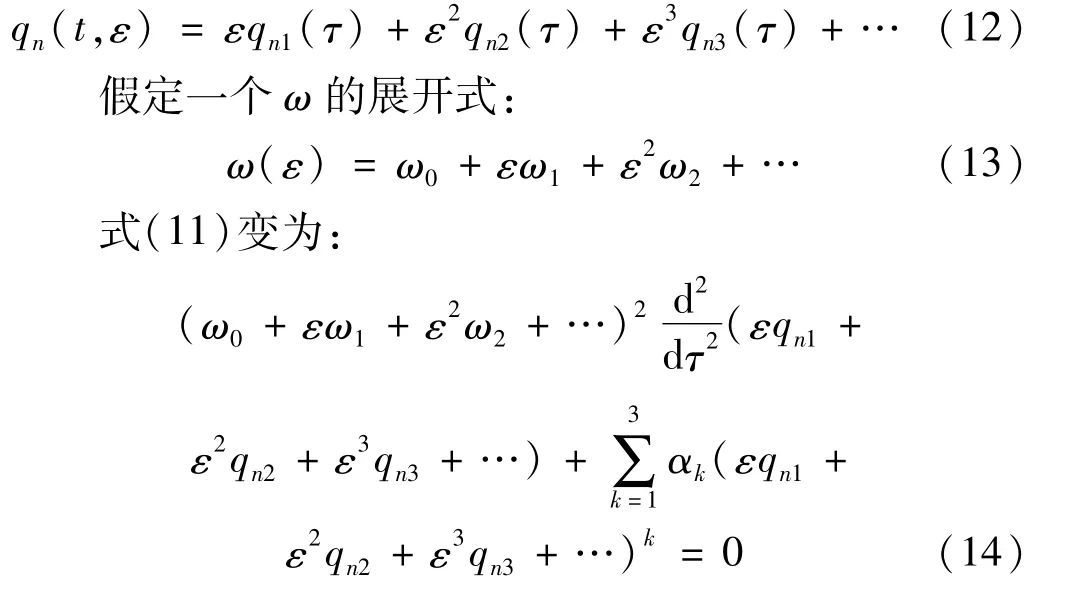
根据ε的各幂次的系数都等于零，可把非线性微分方程化为线性的微分方程组，就得到如下微分方程组：

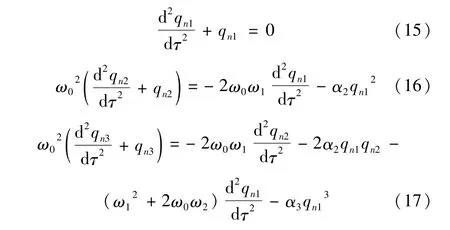
对于初始条件，为简化并且不失一般性，假设初速度为零，只有初位移。

可见斜拉索的非线性自振频率与振幅有关，当振幅较大时要考虑非线性。

3 微分方程的数值解

对于式（11），我们可以把二阶微分方程的初值问题转化为一阶方程组来进行数值求解。利用四阶Runge-Kutta-Gill法［13］，可以编写C++控制台程序，进行求解。

4 算 例

取武汉白沙洲长江大桥C24号斜拉索作为算例，进行分析。该斜拉索的主要参数为［4］：索长为331．013 6 m，弹性模量E＝1．95×105MPa，横截面积A＝6．273×10－3m2，单位长度质量m＝51．8 kg／m，拉索的倾斜角度θ＝24．397 6°，初始张力为2 002 kN，截面惯性矩为3．5×10－6m4。假设：对于一阶振型，跨中的初始振幅是0．95 m；对于二阶振型，1／4跨的初始振幅是0．95 m；对于三阶振型，1／6跨的初始振幅是0．95 m；对于四阶振型，八分之一跨的初始振幅是0．95 m；初始速度为零。

通过计算得知，对于一阶自振，抗弯刚度的影响因素、初拉力的影响因素、重力弦向分力影响因素、索力变化和垂度的线性影响因素分别为α11、α12、α13见表1。

可见初拉力的影响最大，其次是索力变化和垂度的线性影响，再次是重力弦向分力影响，远大于抗弯刚度的影响因素。

各阶自振的影响因素系数见表1。

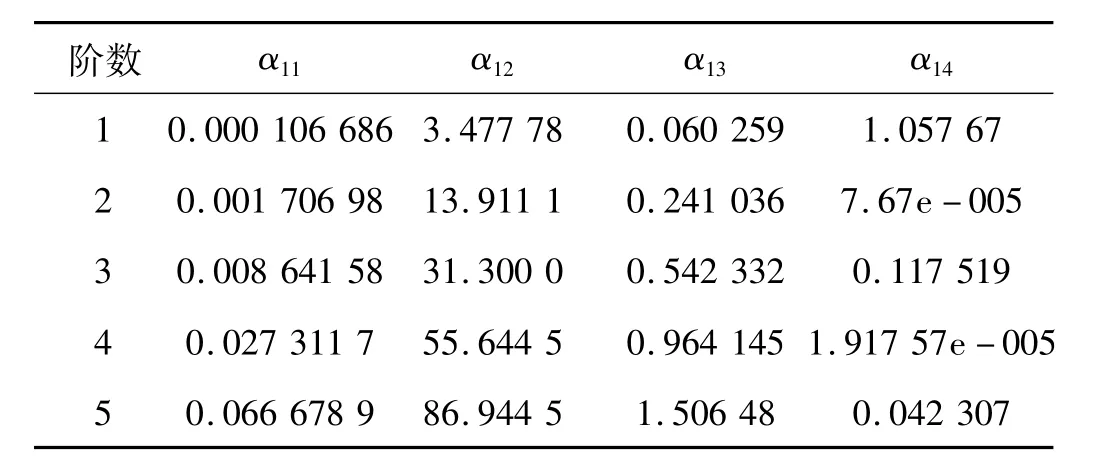
表1 影响因素Tab.1 Influence factor

由表1可知，重力弦向分力影响因素一直都大于抗弯刚度的影响因素，并且从第二阶自振开始，重力弦向分力影响因素已经大于索力变化和垂度的线性影响，因此为了提高斜拉索自振分析的精度，应该要考虑斜拉索的重力弦向分力影响因素。

利用不考虑垂度、索力变化和抗弯刚度影响的标准弦的线性振动理论和本文非线性理论以及数值方法，得到跨中位置一阶自振位移图见图2。

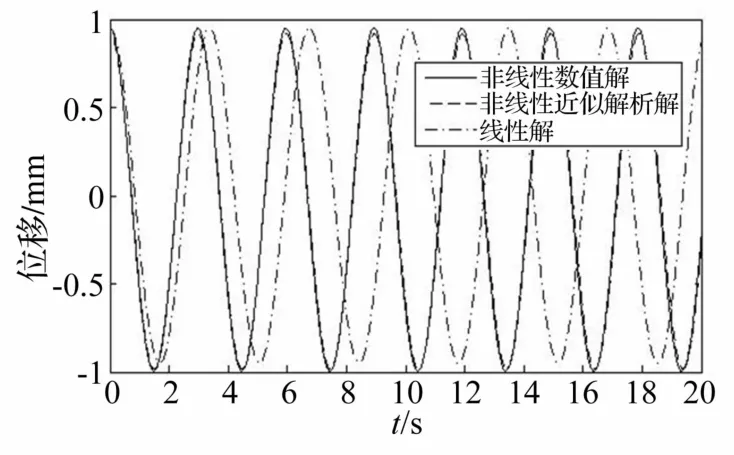
图2 拉索的一阶自振位移图Fig．2 The first order natural vibration displacement of inclined cables

从图2可知，对于一阶自振，非线性近似解析解和非线性数值解基本一致，可见非线性近似解析解是比较精确的。线性解与非线性解有一定的差别，并且由于重力和非线性的影响，非线性解正振幅值为0．950 m，负振幅值为－0．994 9 m，上下不对称，波峰明显小于波谷；而线性解正振幅值为0．950 m，负振幅值为－0．950 m，波峰等于波谷。

本文的非线性为几何非线性，细长杆件（细长梁和索）的几何非线性效应主要包括曲率变化引起的非线性，杆件伸长造成轴力变化引起的非线性和惯性力造成的非线性。本文只考虑一个方向的振动，故没有惯性非线性。曲率变化引起的非线性对应于非线性有限元中的切线刚度矩阵中的大转角矩阵，杆件伸长造成轴力变化引起的非线性对应于几何刚度矩阵。对于两端固定的非线性细长杆件，杆件伸长造成轴力变化引起的非线性占主导地位。索做大幅自由振动时，索必然会伸长，引起非线性。此外索的非线性振动公式考虑了垂度的影响，在重力引起的垂度基础上做振动，从能量的角度来说，索非线性振动考虑了重力势能的影响。线性解没有考虑索的伸张造成的索力变化，也没有考虑垂度，忽略了重力势能的影响。故线性解与非线性解有一定的差别。

用同样的方法得到二阶到五阶自振位移图，见图3～图6。对于二阶振型，图3中的振幅对应于拉索的1／4跨的位置；对于三阶振型，图4中的振幅对应于拉索的1／6跨的位置；对于四阶振型，图5中的振幅对应于拉索的1／8跨的位置。

图3 拉索的二阶自振位移图Fig．3 The second order natural vibration displacement of inclined cables

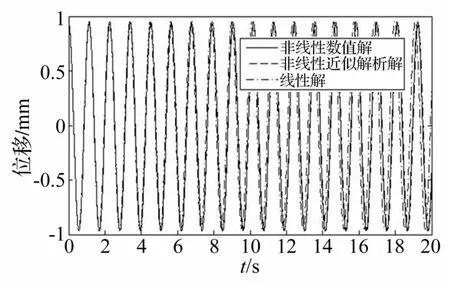
图4 拉索的三阶自振位移图Fig．4 The third order natural vibration displacement of inclined cables

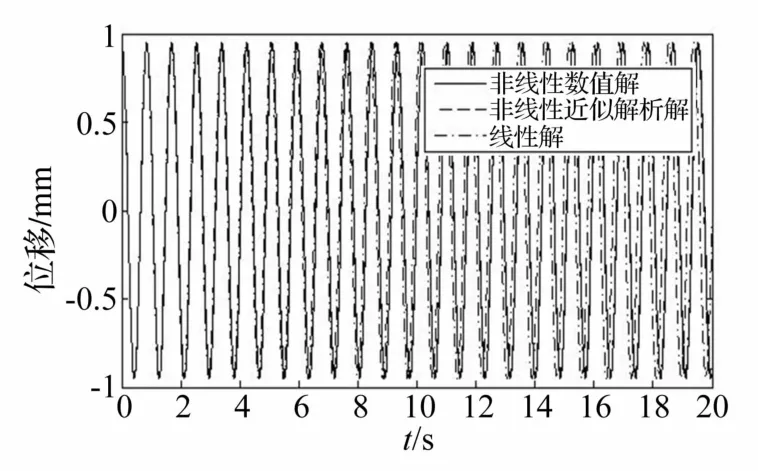
图5 拉索的四阶自振位移图Fig．5 The fourth order natural vibration displacement of inclined cables

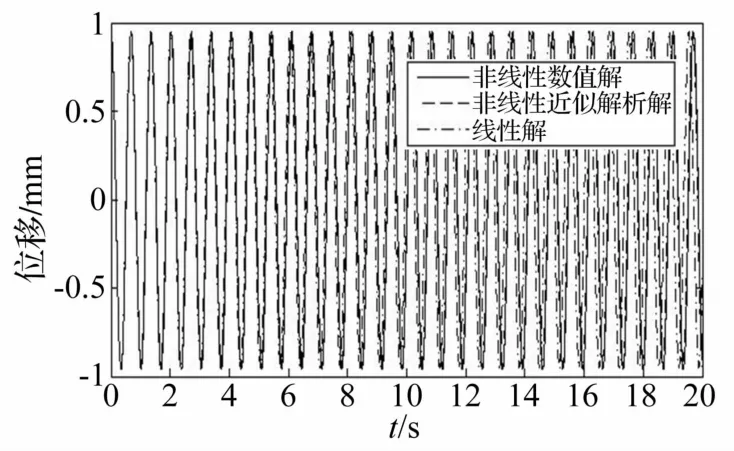
图6 拉索的五阶自振位移图Fig．6 The sixth order natural vibration displacement of inclined cables

从图3～图6可知，对于二阶及其以上阶自振，非线性近似解析解和非线性数值解几乎完全重合，非线性近似解析解是足够精确的；此外，非线性解和线性解差别已经不大了，位移波峰基本等于波谷。

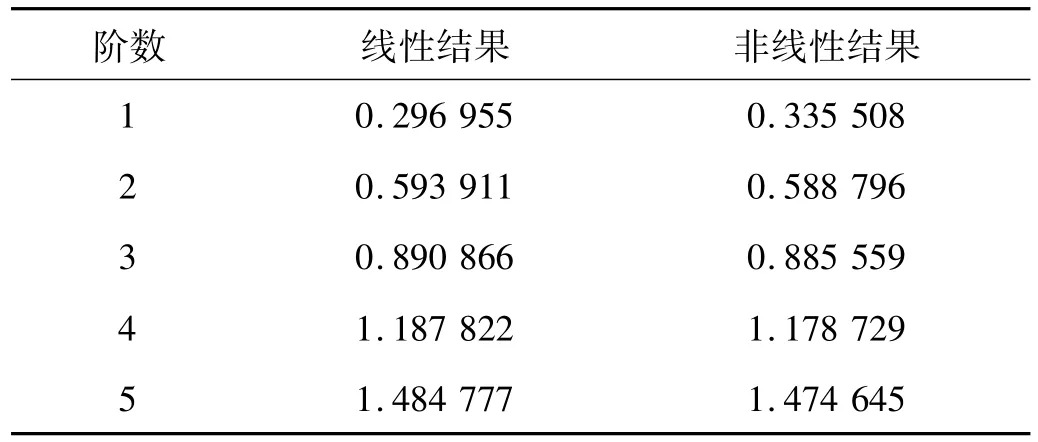
表2 频率对比（Hz）Tab.2 Comparison of frequency

利用标准弦的线性理论和本文的非线性理论以及数值方法，振幅采用上文给出的振幅数值，得到的自振频率见表2。

由表2可以看出，一阶频率的线性解与非线性解差别较大，二阶及以上频率的线性解与非线性解差别较小。该差别原因与图2的线性解和非线性解的差别原因是一样的。

5 结 论

本文通过解析方法和数值方法研究了拉索的大幅横向振动，得出如下结论：

当斜拉索自振振幅较大时要考虑几何非线性对斜拉索自振频率的影响，自振振幅较小时可以不考虑几何非线性。

重力弦向分力影响因素一般都大于抗弯刚度的影响因素，因此为了提高斜拉索自振分析的精度，应该要考虑斜拉索的重力弦向分力的影响。

由于考虑了拉索重力在弦向的分量对斜拉索的振动的影响，采用抛物线来表示垂度悬链线，精度显然不够，故利用幂级数法求解了更精确的垂度微分方程的近似解。

非线性近似解析解和非线性数值解基本一致，所以非线性近似解析解是比较精确的。线性解与非线性解有一定的差别，并且由于重力和非线性的影响，非线性解的位移波峰不等于波谷，这与线性的结果是不一样的。

［1］Max Irine H．Cable structure［M］．Cambridge：The MIT Press，1981．

［2］De SáCaetano E．Cable vibrations in cable-stayed bridges［M］．Zurich：IABSE，2007．

［3］吴晓，黎大志，罗佑新．斜拉索非线性固有振动特性分［J］．振动与冲击，2003，22（3）：37－39．

WU Xiao，LI Da-zhi，LUO You-xin．Nonlinearly natural vibration characteristic analysis of inclined cable［J］．Journal of Vibration and Shock，2003，22（3）：37－39．

［4］刘志军，陈国平．斜拉索在平面内的非线性固有振动特性分析［J］．南京航空航天大学学报，2007，39（1）：65－70．

LIU Zhi-jun，CHEN Guo-ping．Nonlinearly natural vibration characteristic analysis of inclined cable in plane［J］．Journal of Nanjing University of Aeronautics＆Astronautics，2007，39（1）：65－70．

［5］赵跃宇，周海兵，金波．弯曲刚度对斜拉索非线性固有频率的影响［J］．工程力学，2008，25（1）：196－201．

ZHAO Yue-yu，ZHOU Hai-bing，JIN Bo．Influence of bending rigidity on nonlinear natural frequency of inclined cable［J］．Engineer Mechanics，2008，25（1）：196－202．

［6］李金海，李世兵，张松林．考虑斜拉索刚度、垂度、阻尼的非线性运动方程研究［J］．防灾减灾工程学报，2010，30：222－225．

LIJin-hai，LIShi-bing，ZHANG Song-lin．The research on the nonlinear motion equation taking into accounting the stiffness，sag，damp of the inclined cable［J］．Journal of Disaster Prevention and Mitigation Engineer，2010，30：222－225．

［7］付英．基础激励下桥梁斜拉索的非线性振动［J］．动力学与控制学报，2010，8（1）：57－61．

FU Ying．The nonlinear vibration of the inclined cables under the basic stimulation［J］．Journal of Dynamics and Control，2010．8（1）：57－61．

［8］李寿英，黄韬．覆冰斜拉索驰振稳定性的理论研究［J］．振动与冲击，2013，32（1）：122－127．

LIShou-ying，HUANG Tao．Theoretical analysis of galloping stability for stay cables with iced accretions［J］．Journal of Vibration and Shock，2013，32（1）：122－127．

［9］周晓东，阎绍泽，诸福磊．斜拉索1：2内共振非线性特性分析［J］．清华大学学报，2011，51（5）：607－611．

ZHOU Xiao-dong，YAN Shao-ze，ZHU Fu-lei．Nonlinear dynamic analysis of one-to-two internal resonance in taut elastic inclined cables［J］．Tsinghua Univ．2011，51（5）：607－611．

［10］Wagg D，Neild S．Nonlinear vibration with control［M］．New York：Springer，2010．

［11］Nayfeh A H，Mook D T．Nonlinear oscillations［M］．New York：John Wiley＆Sons Interscience，1979．

［12］黄安基．非线性振动［M］．成都：西南交通大学出版社，1993．

［13］高希．数值方法［M］．北京：清华大学出版社，2008．

［14］吉姆辛N J．缆索支承桥梁概念与设计［M］．2版．金增洪，译．北京：人民交通出版社，2002．

Nonlinear free vibration of inclined cables taking into account the effect of chord component of gravity

YUAN Cong-sen，SHEN Rui-li，ZHOU Ling-yuan，LIWei-dong，GUAN Kuai
（School of Civil Engineering，Southwest Jiaotong University，Chengdu 610031，China）

Taking into account the effect of chord component of gravity on the nonlinear free vibration of inclined cables，the nonlinear equations of motion of an inclined cable were developed．The sag differential equation and the nonlinear free vibration equation of the sag were established．The sag differential equation was solved with themethod of power series．Galerkin'smethod was used to convert the nonlinear partial differential equations into ordinary differential equations．The approximate solutions of the equations were obtained with the perturbation method．A corresponding numericalmethod was developed and the resultswere compared with the theoretical solution．The vibration characteristics of inclined cableswere studied considering the variation of cable forces．A new function was chosen to approximate the catenary sag，which is more precise than the parabola function．The total mass of inclined cable increases with the increasing of the length，so the effectof chord componentof gravity on the vibration of inclined cablesmustbe considered．

cable stayed bridges；inclined cables；nonlinear vibration；chord component

TU317

A

10．13465／j．cnki．jvs．2015．12．034

国家自然科学基金资助项目（51178396）

2013－11－01 修改稿收到日期：2014－06－24

袁从森男，博士生，1983年生

沈锐利 男，博士，教授，博士生导师，1963年生