扇形铅粘弹性阻尼器恢复力模型及设计方法研究

吴从晓，徐 昕，周 云，张 超

（广州大学土木工程学院，广州 510006）

扇形铅粘弹性阻尼器恢复力模型及设计方法研究

吴从晓，徐 昕，周 云，张 超

（广州大学土木工程学院，广州 510006）

依据扇形铅粘弹性阻尼器组成材料的特性，给出了阻尼器的构造参数与恢复力学模型之间的关系，推导出该阻尼器恢复力模型公式，给出了阻尼器的设计方法。基于扇形铅粘弹性阻尼器的性能试验结果，对比分析了理论推导结果与试验结果，分析结果表明：扇形铅粘弹性阻尼器的力学性能主要取决于橡胶和铅芯两种材料，可用双线性恢复力学模型对其进行描述；该阻尼器滞回曲线及设计值与试验值吻合度较好，推导的恢复力模型公式合理可行。

扇形；铅粘弹性阻尼器；恢复力模型；设计方法

扇形铅粘弹性阻尼器（SLVD）是一种构造合理，耗能机理明确，滞回性能稳定，耗能能力强的新型复合型耗能阻尼器［1］，该阻尼器利用铅剪切或挤压屈服后产生的塑性变形和粘弹性材料的剪切滞回变形进行耗能，充分利用粘弹性阻尼器在小变形下的耗能作用和铅剪切、挤压型阻尼器屈服位移小、屈服后刚度小、自恢复性能好的优点，可用于结构的地震反应控制和风振反应控制。通过对扇形铅粘弹性阻尼器的有限元分析和滞回性能试验，得出该阻尼器耗能机理明确，构造合理，滞回性能稳定［2］。

扇形铅粘弹性阻尼器可直接安装在结构框架柱与梁之间的节点部位，不需使用额外的连接支撑，体积小，不影响建筑使用空间。该阻尼器的耗能性能、承载力、刚度及阻尼特性等受铅芯橡胶材料性能和构造设计参数的影响较大，准确掌握该阻尼器的恢复力模型，用简捷合理的公式描述其力与位移的关系，是该阻尼器设计的一个重要问题。在扇形铅粘弹性阻尼器耗能性能数值模拟和试验研究的基础上，依据扇形铅粘弹性阻尼器组成材料的特性，给出了阻尼器的构造参数与恢复力学模型之间的关系，推导出该阻尼器恢复力模型公式，最后通过试验验证了该力学模型的正确性和合理性。

1 扇形铅粘弹性阻尼器构造

扇形铅粘弹性阻尼器由粘弹性材料（橡胶）、薄钢板、剪切钢板、约束钢板、铅芯和连接板所构成［3］。橡胶层和薄钢板经高温高压硫化成复合弹性体，复合弹性体、约束钢板和剪切钢板均为同心的扇形，两连接板外侧面的延长线交于该圆心。铅芯的数量和直径大小的设置根据阻尼器性能要求确定，其构造见图1所示。

图1 扇形铅粘弹性阻尼器构造Fig．1 Constitution of SLVD

2 扇形铅粘弹性阻尼器受力变形

2.1 铅芯受力变形

扇形铅粘弹性阻尼器中的铅芯在小变形时就会发生剪切屈服，并且屈服后刚度很小可忽略不计，为此，铅芯可看成理想弹塑性固体，其本构模型如式（1）所示，可采用理想弹塑性模型［4－5］对铅芯的力学关系进行描述（见图2）。

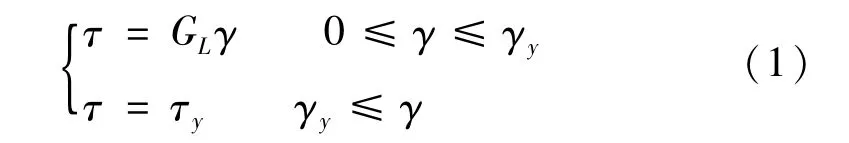
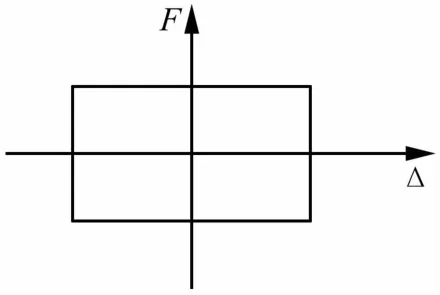
图2 理想弹塑性力学模型Fig．2 Ideal elastic-plastic mechanicsmodel

式中：GL为铅芯剪切模量；γy为铅芯屈服剪应变。

扇形铅粘弹性阻尼器中的铅芯两端嵌入约束钢板中并由中间剪切钢板带动剪切变形耗能，图3为圆柱型铅芯受力变形图，基于铅芯的理想弹塑性模型，假设横截面各点处剪切变形均匀相等，即铅芯横截面各点处材料屈服同时发生，且在小变形下，忽略弯曲应力和轴向应力的影响。

根据能量守恒原理，外力F所做的功W等于铅芯变形所耗散的能量U，即W＝U：

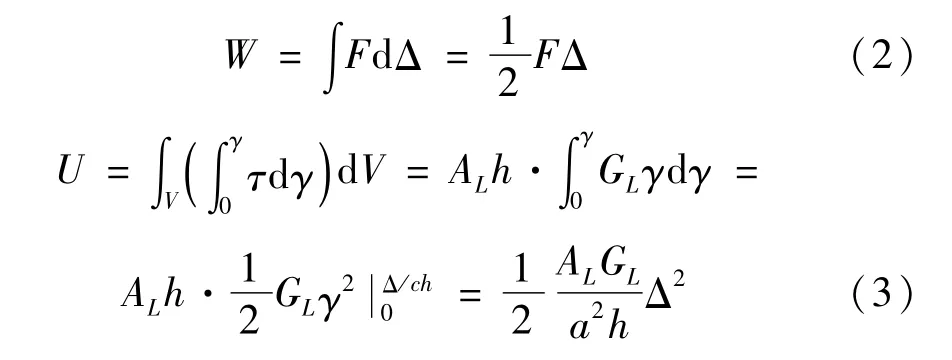
式中：W为剪力F所做的外力功；U为铅芯变形耗能；F为铅芯剪力；Δ为剪切位移，D为铅芯直径；H为铅芯总高度；Hs为剪切钢板或约束钢板厚度；h为铅芯屈服位移计算高度；γ为剪应变；KL为铅芯剪切刚度；AL为铅芯横截面积；GL为铅芯剪切模量；ρ为变形影响系数；τy为铅芯屈服应力。

由近似几何关系可得γ＝tanγ，铅芯在变形过程中，铅芯的直径D和高度H之比（D／H＝径高比）对铅芯变形有一定的影响，为此，引入该影响系数a，即：γ＝tanγ＝Δ／aH；扇形铅粘弹性阻尼器中铅芯上下两端嵌固在约束钢板中，并不产生塑性变形，所以计算屈服位移时铅芯高度取值应为h＝（H－2Hs）。

由W＝U，并设ρ＝a2，可得：

由式（4）和式（5）可得单铅芯扇形铅粘弹性阻尼器剪切刚度和屈服位移：

图3 铅芯构造及剪切变形受力图Fig．3 The structure and shear force diagram of lead core

2.2 橡胶受力变形

扇形铅粘弹性阻尼器中的粘弹性材料采用了天然橡胶，橡胶材料受力以后，其本构关系呈非线性［6］。

图4为扇形铅粘弹性阻尼器中剪切钢板在梁柱节点区剪切变形受力示意图，梁柱节点侧向变形带动在安装在梁底部的扇形剪切钢板剪切变形，将图中扇形剪切钢板与复合弹性体粘结区域（图中扇形实线部分）近似等效为面积相等的矩形区域（图中矩形虚线区域），等效的矩形钢板带动复合弹性体沿其长度和宽度方向的剪切力均为F＝βKvΔ，所以可合成扇形剪切钢板的剪切力为式（8），方向如图4所示。

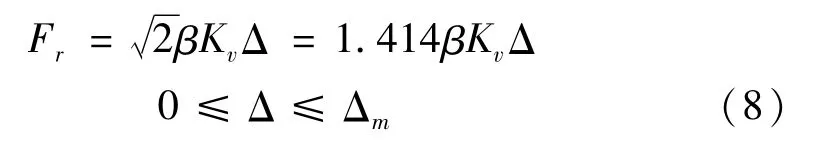
式中：β为橡胶材料硬度修正系数，F为矩形剪切钢板沿长度或宽度方向剪切力；Fr为扇形剪切钢板剪切力的合成。

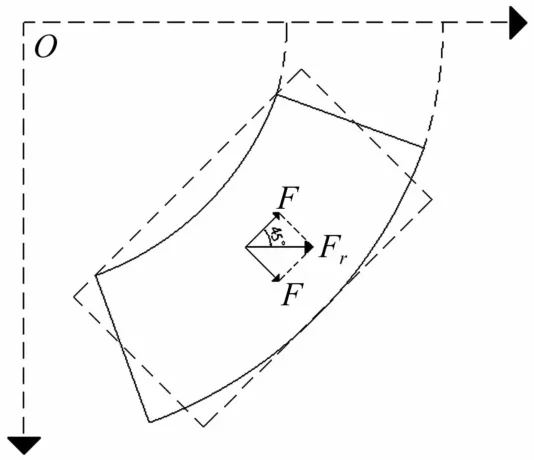
图4 扇形剪切钢板所受剪切力的合成Fig．4 Shear force of sector shear plate

由于复合弹性体的剪切刚度Kr受诸多因素影响，考虑到复合弹性体主要以剪切变形为主的变形特征，可按纯剪切情况计算其剪切刚度［7］，并结合式（8）得到其复合弹性体剪切刚度计算公式为：

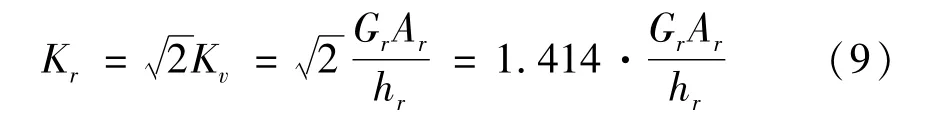
式中：F为橡胶剪切力；Kv为复合弹性体单向剪切刚度；Kr为扇形复合弹性体剪切刚度；Δ为剪切位移；β为橡胶材料硬度修正系数；Ar为复合弹性体有效剪切面积；Gr为橡胶剪切模量；hr为单块复合弹性体橡胶层总高度。

3 扇形铅粘弹性阻尼器恢复力模型

由扇形铅粘弹性阻尼器的滞回曲线和骨架曲线的模拟和试验分析可知，扇形铅粘弹性阻尼器的力学性能主要取决于橡胶和铅芯两种材料的性质及组合性能，其滞回环相当于两种材料力学模型的叠加，呈现平行四边形（见图5）。

在一定的荷载范围内，扇形铅粘弹性阻尼器在循环荷载作用下，铅芯发生理想弹塑性变形，而橡胶保持超弹性变形，所以该阻尼器的力学行为可近似的看成是双线性［8］（见图6）。

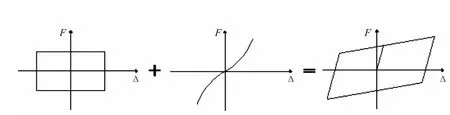
图5 扇形铅粘弹性阻尼器滞回模型Fig．5 Hysteretic model of the SLVD

图6 SLVD双线性力学模型Fig．6 Bilinearmodel of the SLVD

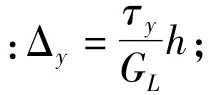
弹性阶段（0≤Δ≤Δy）：

式中：K1为单铅芯初始刚度；K2为屈服后刚度；Ke为等效刚度；hr为单块复合弹性体中橡胶层总厚度，hr＝nrtr；nr为单块复合弹性体中橡胶层层数；tr为单层橡胶层厚度；Ar为复合弹性体有效剪切面积，Ar＝（R2－r2）－nLAL；β为橡胶材料硬度修正系数，其取值按表1取值［10］。

表1 橡胶材料硬度系数（β值）Tab.1 Hardness coefficient of Rubber material

4 扇形铅粘弹性阻尼器设计方法

4.1 设计荷载

设计承载荷载是用于验算结构在小震作用下阻尼器是否处于弹性状态，在小震作用下阻尼器所受的荷载小于阻尼器的设计承载荷载就说明处于弹性状态。考虑到阻尼器钢材供应的公差、钢材及铅芯屈服点的离散、其他材料性能的退化、存在的摩擦、泊松效应和包辛格效应等因素的影响，该阻尼器设计承载荷载采用阻尼器0．9倍的屈服荷载，即：

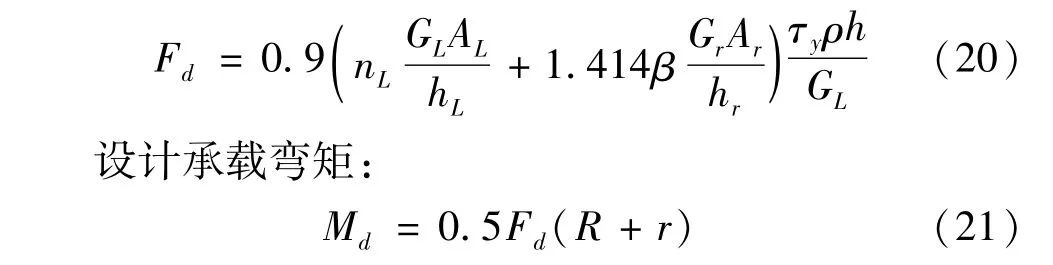
在风荷载或小震与其它静力荷载组合下最大剪力F或弯矩设计值M应满足下式：

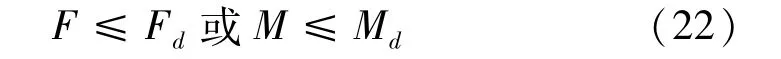
式中：Fd为设计承载剪力；Md为设计承载弯矩；R为扇形外径；r为扇形内径。

4.2 屈服荷载

屈服承载荷载是用于保证结构在中震作用下阻尼器进入耗能状态，在中震作用下阻尼器所受的荷载大于阻尼器的屈服承载荷载就说明处于耗能状态，屈服承载荷载用于结构的弹塑性分析，是阻尼器首次进入屈服耗能的荷载值。其屈服承载剪力：

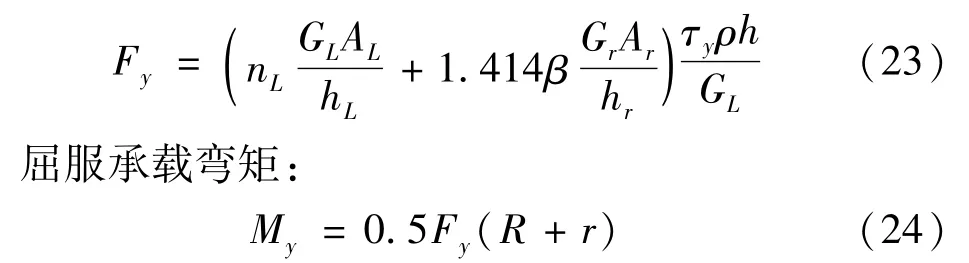
式中：Fy为屈服承载剪力；My为屈服承载弯矩。

4.3 极限荷载

极限承载荷载是用于验算结构在大震作用下阻尼器是否破坏退出工作，也可用于验算阻尼器的节点及连接设计。根据分析和试验研究的结果，考虑以该阻尼器1．25nrtr（1．25倍的单层复合弹性体厚度）应变幅值作为其极限位移值，在此状态下阻尼器提供的即为极限承载荷载。

式中：Fu为极限承载剪力；Mu为极限承载弯矩。

4.4 阻尼器刚度

扇形铅粘弹性阻尼器的初始刚度主要取决于铅芯和橡胶的刚度总和，铅芯的直径对其影响较大，初始刚度可由式（27）和式（28）确定。其剪切初始刚度：

扇形铅粘弹性阻尼器的屈服后刚度主要取决于橡胶的剪切刚度，橡胶的剪切模量对其影响较大，屈服后刚度可由式（29）和式（30）确定。其剪切屈服刚度：

5 扇形铅粘弹性阻尼器性能试验及设计方法验证

根据以上设计方法设计了二组扇形铅粘弹性阻尼器试件（见图7），设计参数见表2，对其进行性能试验，试验结果如文献［11］。

试验所得滞回曲线和理论分析结果见图8。通过对比分析试验滞回曲线及理论分析可知，试验和理论设计所得滞回曲线吻合较好，理论设计结果未考虑材料变形疲劳积累效应、性能退化等因素，试验结果在正反向卸载段均有光滑的过渡段，而理论设计结果无过渡段。总体分析可知试验研究和理论设计的结果吻合较好，设计结果基本能够反映该阻尼器的滞回性能特点，说明采用该理论设计方法对扇形铅粘弹性阻尼器进行设计是可行合理的。

图7 扇形铅粘弹性阻尼器试件实体图Fig．7 Sector Lead Viscoelastic Damper（SLVD）specimens

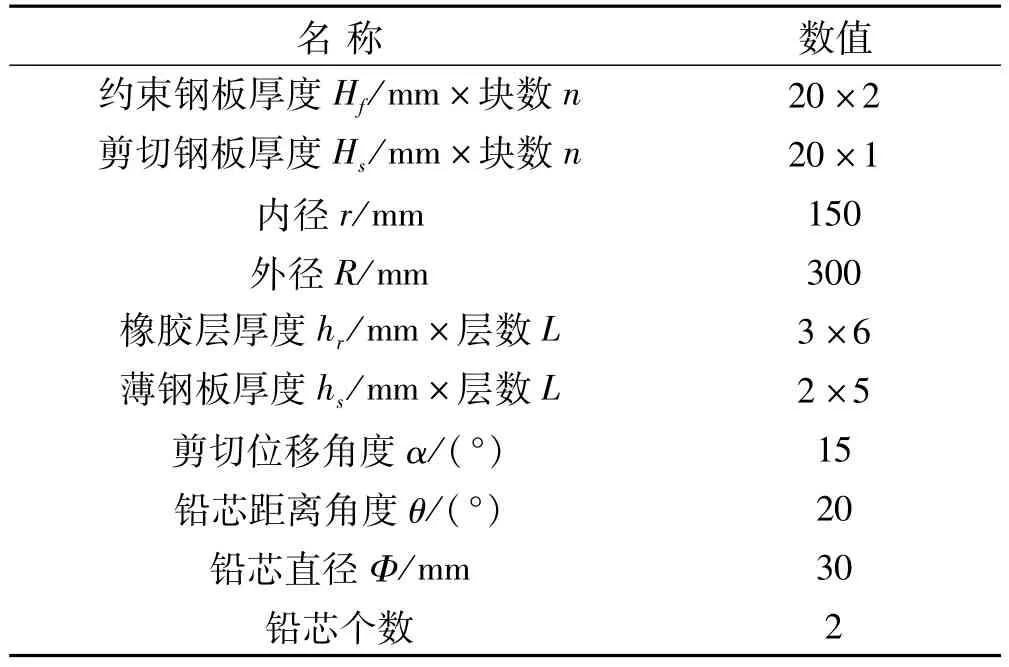
表2 扇形铅粘弹性阻尼器设计构件的设计尺寸及参数Tab.2 Design parameters of SLVD

图8 SLVD构件试验结果与理论设计结果对比Fig．8 Comparison of test results and the theoretical design results of SLVD component

6 结 论

通过对扇形铅粘弹性阻尼器的恢复力模型及设计方法进行研究，得出以下结论：

（1）扇形铅粘弹性阻尼器的力学性能主要取决于橡胶和铅芯两种材料，可用双线性恢复力学模型对其进行描述；

（2）扇形铅粘弹性阻尼器试验所得的滞回曲线与理论分析结果吻合度较好，推导出的恢复力模型公式合理可行。

［1］周云，邹征敏，邓雪松．梁柱节点加固扇形铅粘弹性阻尼器：中国，CN201560506U［P］．2010．

［2］吴从晓，周云，徐昕，等．扇形铅黏弹性阻尼器滞回性能试验研究［J］．建筑结构学报，2014，35（4）：199－207．

WU Cong-xiao，ZHOU Yun，XU Xin，et al．Experimental investigation on hysteretic performance of sector lead viscoelastic damper［J］．Journal of Building Structures，2014，35（4）：199－207．

［3］周云，徐昕，邹征敏，等．扇形铅粘弹性阻尼器的设计及数值仿真分析［J］．土木工程与管理学报，2011，28（2）：1－6．

ZHOU Yun，XU Xin，ZOU Zhen-min，et al．Design and numerical simulation analysis of sector lead viscoelastic damper［J］．Journal of Civil Engineering and Management，2011，28（2）：1－6．

［4］李冀龙，欧进萍．铅剪切阻尼器的阻尼力模型与设计［J］．工程力学，2006，23（4）：67－73．

LI Ji-long，OU Jin-ping．Damping force models and designs of lead shear dampers［J］．Engineering Mechanics，2006，23（4）：67－73．

［5］李冀龙．金属阻尼器的阻尼力模型［D］．哈尔滨：哈尔滨工业大学，2002．

［6］张少实，庄茁．复合材料与粘弹性力学［M］．北京：机械工业出版社，2007．

［7］周福霖．工程结构减震控制［M］．北京：地震出版社，1997．

［8］周云，徐赵东，邓雪松．铅粘弹性阻尼器的计算模型．地震工程与工程振动［J］．2000，20（1）：120－124．

ZHOU Yun，XU Zhao-dong，DENG Xue-song．Calculating models of lead viscoelastic dampers［J］．Earthquake Engineering and Engineering Vibration，2000，20（1）：120－124．

［9］周云．粘弹性阻尼减震结构设计［M］．武汉：武汉理工大学出版社，2006．

［10］唐家祥．建筑结构基础隔震［M］．武汉：华中理工大学出版社，1993．

［11］徐昕．新型扇形铅粘弹性阻尼器性能及应用研究［D］．广州：广州大学，2012．

Restoring forcemodel and design method of sector lead viscoelastic damper

WU Cong-xiao，XU Xin，ZHOU Yun，ZHANGChao
（School of Civil Engineering，Guangzhou University，Guangzhou 510006，China）

Based on the material characteristics of the sector lead viscoelastic dampers（SLVD），the relationship between appropriate structural parameters and restoring force equation was given，and the restoring forcemodel of SLVD was derived．The design method of the damper was given out．The performances of the damper were tested under low frequency cyclic load．The results were compared with those of the numerical simulation and the test．The investigation results indicate that：themechanical properties of the sector lead viscoelastic damper aremainly depended on rubber and lead and the symmetric bilinearmodel can be used to describe the restoring force of the damper．The experimental and numerical simulation results of SLVD hysteretic curve are in good agreement．It is feasible to adopt the given model to simulate the damper element．

sector；lead viscoelastic damper；restoring forcemodel

TU352．1

A

10．13465／j．cnki．jvs．2015．12．004

国家自然科学基金（51208128）；广东省高等学校科技创新项目（2013KJX0145）；城市与工程安全减灾教育部重点实验室项目；广州市场珠江科技新星专项（1517000272）

2014－03－10 修改稿收到日期：2014－06－13

吴从晓 男，博士，讲师，1981年生