一种新型调谐质量阻尼器的试验研究

施卫星，何 斌，李晓玮，鲁 正

（1．同济大学结构工程与防灾研究所，上海 200092；2．同济大学建筑设计研究（集团）有限公司，上海 200092）

一种新型调谐质量阻尼器的试验研究

施卫星1，何 斌1，李晓玮2，鲁 正1

（1．同济大学结构工程与防灾研究所，上海 200092；2．同济大学建筑设计研究（集团）有限公司，上海 200092）

用填充颗粒群的盒子代替调谐质量阻尼器的质量块，形成一种新型调谐质量阻尼器。通过对比单自由度排架不附加、附加该新型调谐质量阻尼器的自由振动，白噪声激励以及实际地震输入下的振动台试验，考察了该新型阻尼器对结构的减振控制效果。试验研究表明：颗粒的填充率对振动衰减影响明显，表现出双峰值的曲线特征；颗粒质量对衰减率的影响不明显，实际工程可以采用轻质颗粒材料；输入地震波能量与衰减率呈抛物线形。试验还从振型特性方面表明采用调谐颗粒阻尼器有利于减轻结构振动响应。

新型调谐质量阻尼器；振动台试验；结构振动控制；影响因素

单摆式调谐质量阻尼器（TMD）主要由摆绳、质量块和阻尼器组成。其工作原理是：调整单摆的摆长使其自振频率接近主结构被控频率，当外力作用在主结构上，单摆随之产生与主结构相反的运动，施加反作用力于主结构上，从而控制结构的振动。输入结构的振动能量通过单摆TMD的阻尼器消散［1］。单摆式TMD已经越来越多地应用于高耸结构如超高层、风力发电塔等，以及细长结构如人行桥。传统TMD的阻尼系统大多采用黏滞阻尼器。黏滞阻尼器的出力与活塞孔直接相关，长时间使用会使活塞孔扩大影响阻尼系数，而且黏滞阻尼器使用中经常漏油。所以黏滞阻尼器并不是为TMD提供阻尼最好的方法。

颗粒阻尼器将装有金属或者其他材料颗粒的容器附着在结构振动较大的部位，利用颗粒之间以及颗粒与容器壁之间的碰撞、摩擦以及声音辐射等机理来消耗系统振动能量。该技术具有减振频带宽、温度不敏感、耐久性好、易于应用在恶劣环境等优点，在土木工程界有良好的应用前景［2－3］。本文尝试将填充有颗粒群的盒子代替单摆TMD的质量和黏滞阻尼器，形成一种新型调谐颗粒式质量阻尼器［4］，并试验验证其减振效果，研究减振率影响因素的规律。

1 试验模型及试验过程

试验主体结构采用单自由度排架，为了调节结构的自振频率至1 Hz左右，在结构的顶部配加6 kg的质量块，见图1。经测试，该排架结构自振频率为1．37 Hz。填充颗粒的盒子通过四根细线垂直悬吊在结构顶部。盒子横截面尺寸相同，均为60 mm×60 mm，长度分别为80 mm、100 mm、120 mm、140 mm和160 mm。颗粒采用10 mm的不锈钢球、15 mm的玻璃球、20 mm的陶瓷球以及20mm的钢球。5个尺寸的盒子和四种颗粒（见图1）。

图1 振动台试验主体结构、盒子、颗粒以及振动台面Fig．1 Themain structure，boxes，particles and the surface of platform in the shaking table tests

试验采用的Quanser振动台主要由PC控制系统、电源驱动系统（UPM）、振动台面以及数据采集卡（DAC）组成。台面可以沿两个金属轴单方向移动，当台面在金属轴的中间位置时，向两边移动的位移限值为7．26 cm。振动台的监测系统包括急停器、台面加速度传感器和位移传感器。将地震波或者正弦波扫频数据输入振动台控制软件，软件可以自动转化为台面位移来驱动台面运动，不同能量的地震波需要以位移幅值来控制。振动台面见图1。

为了研究新型调谐质量阻尼器的减振效果，以及颗粒质量、颗粒填充率、激励频谱特性和激励能量大小对减振效果的影响［5］，分别对不附加阻尼器和附加不同种类阻尼器的排架模型进行了自由振动试验、白噪声［6］和实际地震波输入下的振动台试验［7］。试验中采用了三种地震波，分别是El Centro波（1940，SN）、Kobe波（1995，SN）和上海人工波（SHW2，1996）［8］。不同工况下盒子尺寸和颗粒形式见表1，输入的白噪声和地震波位移幅值见表2。

2 试验结果

2.1 自由振动试验

自由振动试验采用给结构施加初始位移的方法，主要目的是为了采集自由振动加速度时程数据，进而分析各工况下的频率特性，并大致了解调谐颗粒阻尼器的工作状态，为振动台试验做准备。图2所示为原排架结构、悬吊单摆质量（128 g）以及悬吊填充颗粒（4个20 mm钢球）的盒子之后结构自由振动的加速度时程曲线。该时程曲线均是在排架顶部具有相同初始位移条件下测得，可以看出悬挂质量块之后的结构振动衰减好于不加阻尼器的原结构，而悬挂颗粒填充的盒子之后的结构振动具有明显的衰减。说明当选用适当参数的新型调谐质量阻尼器后，结构的振动响应可以得到明显降低。由图2可知，悬吊质量之后的结构具有明显两个频率，符合两自由度体系的周期与振型特征，即附加调谐质量阻尼器之后，结构会在原频率附近拆分成两个频率。但是悬吊调谐颗粒阻尼器之后，两自由度周期的特征却不明显。当两个振型的频率过于接近时，或者某个频率下的振型输入能量过小不足以激发其振动时，便只能识别出某一个频率。图2中悬挂新型调谐质量阻尼器的结构第二周期明显，第一周期没能识别出来，说明盒子的运动方向与主体结构相反的第二阶振型占绝对优势，而盒子与结构同向运动的第一阶振型十分微弱。调谐质量阻尼器的减振原理正是利用了阻尼器与主体结构的反相位运动，以达到减振效果，所以填充颗粒之后的新型调谐质量阻尼器对减振效果更有利。

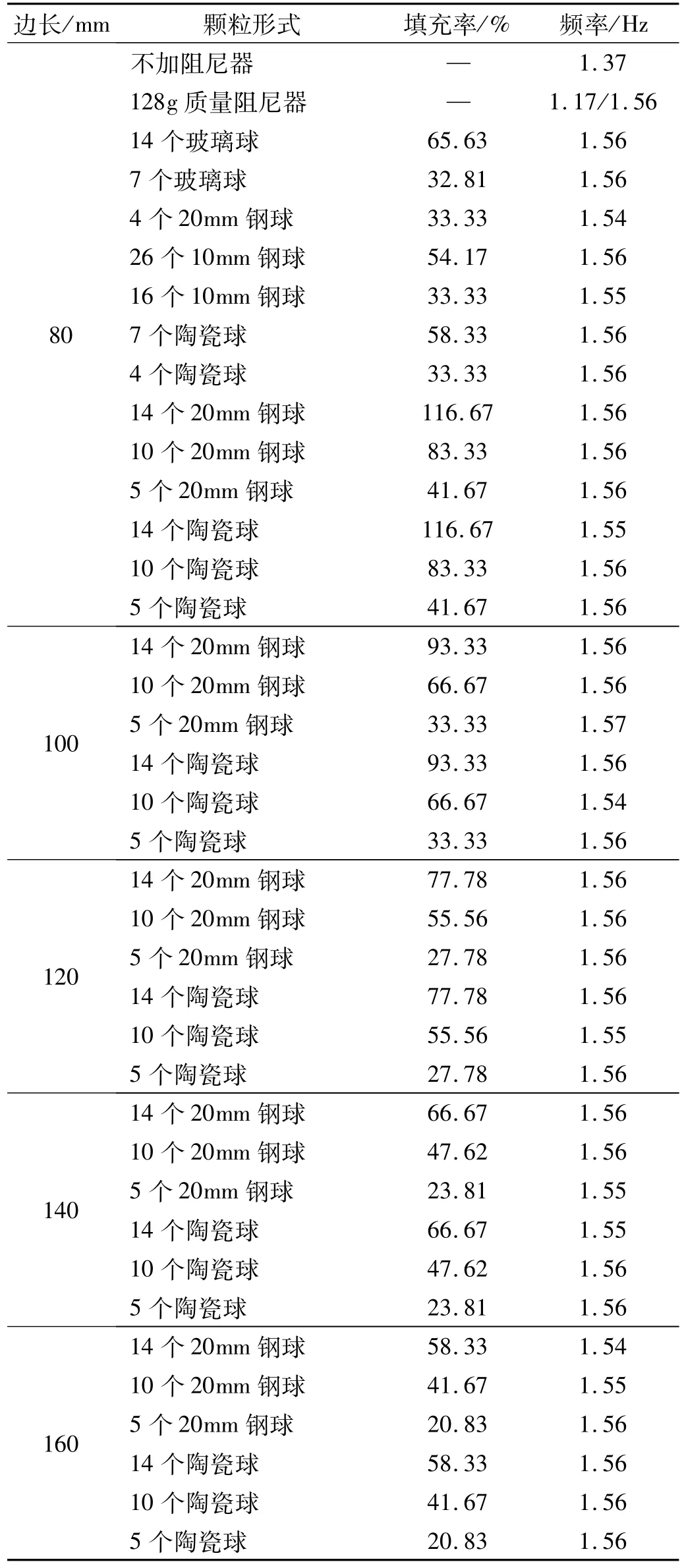
表1 振动台试验的不同工况（盒子尺寸：60mm*60mm*边长）Tab.1Working conditions of the shaking table tests（Box Size：60mm*60mm*length）

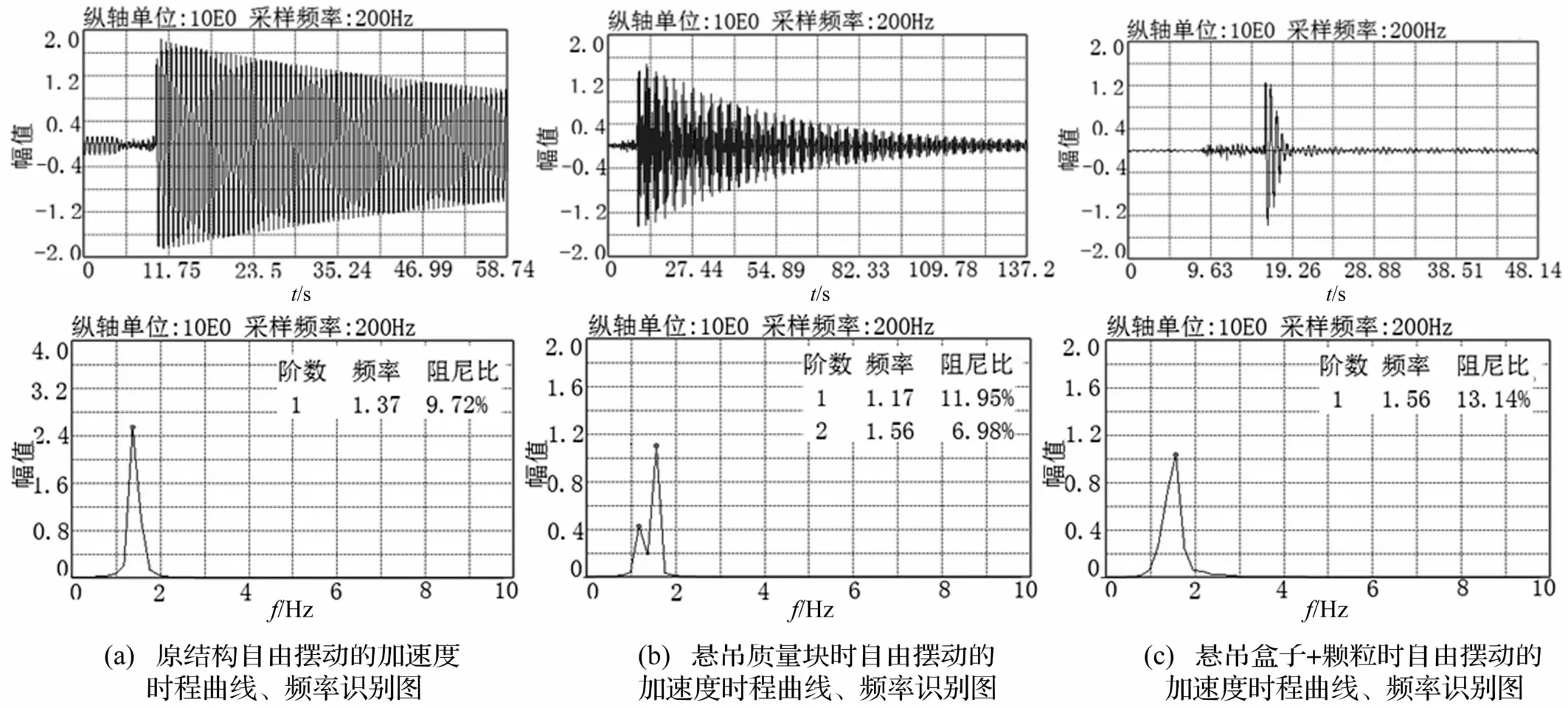
图2 加速度时程曲线及频率识别Fig．2 Acceleration time history and frequency identification chart

2.2 地震波激励试验

排架顶部加速度时程曲线中的最大加速度值仅代表某一时刻结构的动力响应，而振动衰减率是能量减小的概念。均方根加速度比较真实的表现了结构振动能量的大小，所以本文采用均方根加速度用于计算衰减率。衰减率定义为：

如果对比某一种颗粒形式（比如14个、10个、5个20mm钢球或者陶瓷球这6种形式），分别使用长度为80 mm，100 mm，120 mm，140 mm和160 mm的盒子时，可以保证质量不变而填充率变化。对每种阻尼器形式进行不同幅值的白噪声和地震波试验（25种输入激励），可以得到150组数据。每组数据有5个数据点，是在相同质量和激励作用下不同填充率对应的衰减率。对这5个数据点从1～5进行排序：1表示在本组数据中衰减率最高，5表示在数据组中衰减率最低，2、3、4依次表示为在本组中衰减率较高、居中以及较低。最后对这150×5个数据点按照填充率范围分类（0%～20%、20%～30%、30%～70%、70%～80%和80%以上6个填充率范围），统计每个填充率范围内衰减率排序1、2、3、4、5出现的次数和该排序在本范围内出现的概率，得到结果见图3。填充率为颗粒群的竖向投影面积与盒子底部面积的比值，当颗粒数量较多而堆叠时，填充率大于100%。

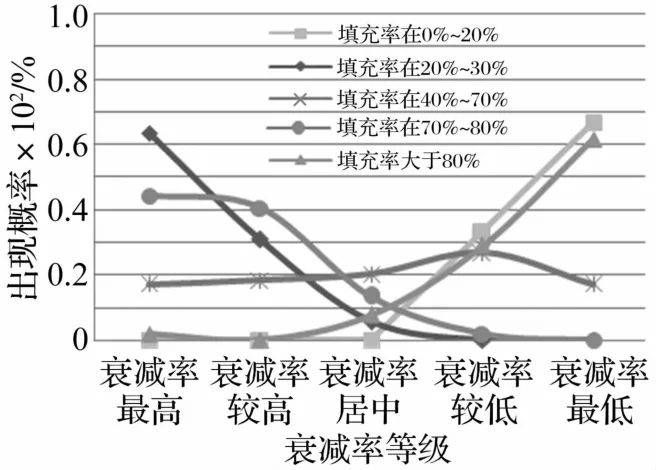
图3 填充率对振动衰减的影响规律Fig．3 The effect of filling ratio on vibration reduction

图4 填充率在55%～60%之间时，质量与衰减率的关系Fig．4 The effect of particlemass on vibration reduction while the filling ratio is between 55%～60%

由图3可见当填充率处于20%～30%和70%～80%之间时，衰减率最高的可能性大，所以颗粒的填充率应尽量处于其中。当填充率处于0%～20%、30%～70%和80%以上时，衰减率最低的概率比较大，所以颗粒的填充率应尽量避免处于这些范围。试验中发现，当填充率较小（20%～30%）时，颗粒在相互碰撞之前有较大的运动空间。碰撞时小球具有较高的速度，即碰撞能量较大，充分的有效碰撞是提高颗粒阻尼器减振效率的有效方法，所以此时趋向具有较大的衰减率。但是当填充率过分小时，颗粒之间大部分时间花在运动过程中，而碰撞次数较少，会影响衰减率。如图3，填充率处于0%～20%时衰减率会很低，但是填充率处于20%～30%填充率可能会比较高。当填充率比较大（70%～80%）时，颗粒之间只要满足有足够的空间满足其初始运动，但是间距又不是太大，在相同的时间内碰撞次数增加，从而消耗能量较多，衰减率较大。但是填充率太大，颗粒之间在碰撞之前没有足够的运动空间，反而不能产生有效碰撞。如图3，当填充率大于80%以上，衰减率会很低，但是如果衰减率处于70%～80%之间，衰减率却会比较高。试验中同样发现，相比其他情况填充率处于30%～70%中间时颗粒运动更显混乱。即不同颗粒的运动相位不同，难以形成颗粒流的形式，则有效碰撞次数会大大减少，造成衰减率较低。总之，填充率过小或者过大，或者处于这两种最优填充率之间时都会对衰减率造成不利影响，应加以避免。

当填充率的变化处于较小范围时，比如20%～30%或55%～60%，可以认为填充率的变化不影响结构振动的衰减率。控制填充率不变可以观察其他因素对衰减率的影响规律。由图4、图5可见，质量对填充率的影响不明显，即并不是单纯增大或者减小质量可以增加衰减率。忽略试验误差后，在相近的填充率下，质量和衰减率基本呈一条平直线关系，个别试验工况下会呈不规则的波浪线形。而且，当地震激励强度较小时，这种不规则的线形越明显，随着地震激励强度的增大，质量与衰减率关系越发趋于一条直线。原因可能是激励过小时，尚不足以激发颗粒的充分运动和碰撞，所以表现出强烈的不确定性。当激励强度增大后，小球碰撞足够充分，阻尼器的作用尽量发挥出来以后，质量与衰减率的规律才能完全表现出来。

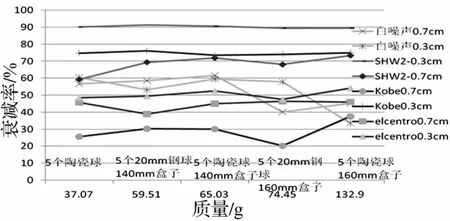
图5 填充率在20%～30%之间时，质量与衰减率的关系Fig．5 The effect of particlemass on vibration reduction while the filling ratio is between 20%～30%

图6 地震波能量谱Fig．6 Energy spectrum of seismic wave

在相同填充率（33%和58%）时，不同地震工况的衰减率排序大致相同。表2所示为某种地震波，不同位移幅值下衰减率的排序。可以看到，输入激励的位移幅值与衰减率是非线性的关系，即激励能量大并不意味着衰减率大，反而最大的衰减率发生在某个处于中间能量的激励处。试验中发现，当激励较小时，外界输入阻尼器的能量过小不足以激发颗粒的运动，颗粒阻尼器不能够充分发挥其减振的作用。但是当激励过大时，盒子发生大角度摆动。由于采用了只受拉绳索悬吊，盒子摆动剧烈时绳子并不是一直拉紧的，此时已不再符合单摆的运动形式。这种反常运动对衰减率的影响是不利的。如果激励能量再大，盒子会与两侧壁碰撞，短时间内盒子的运动变的混乱，更不利于振动的衰减。

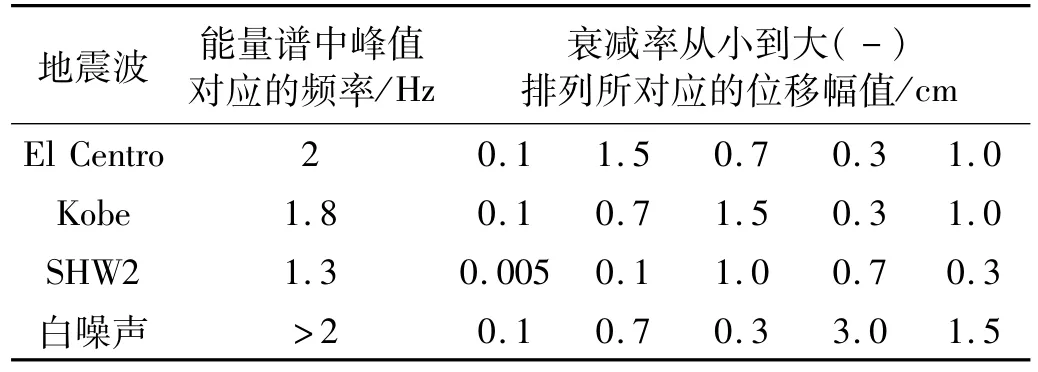
表2 填充率接近33%、58%时，地震波能量与衰减率关系Tab.2 The relationship between the energy and vibration reduction while havi

从图5（a）、图5（b）还可得到，对于相同的颗粒形式，相同的地震波位移幅值，不同的地震波对衰减率的影响也是不同的。例如地震波位移幅值为0．1 cm时，结构衰减率排序为SHW2＞白噪声＞El Centro＞Kobe；当地震波位移幅值为0．3 cm时，结构衰减率排序SHW2＞白噪声＞El Centro＞Kobe；当地震波位移幅值为0．7cm时，结构衰减率排序为SHW2＞Kobe＞白噪声＞El Centro。总的来说，对于相同的地震波位移幅值，输入SHW2和白噪声的波形，结构的衰减率比较高，而输入El Centro波和Kobe波时衰减率比较低。从图6能量谱中观察到SHW2的峰值主要集中在1．3 Hz左右，与结构的自振频率1．37 Hz比较接近，而El Centro波和Kobe波的能量谱峰值集中在2 Hz和1．8Hz左右，稍偏离了结构的自振频率，说明当外界激励的频率越接近结构的自振频率，阻尼器的减振效果越好。这一结论正好与传统调谐质量阻尼器的结论相同，说明调谐颗粒阻尼器具有与调谐质量阻尼器相同的频率特性。白噪声的能量谱峰值处的频率离结构频率也较远，但是衰减率较大的原因可能是相同地震波位移幅值下，白噪声输入结构的能量更多，进而颗粒的运动得到了充分激发，使得减振率增大。

3 结 论

通过以上试验结果的分析可以得出：安装新型调谐质量阻尼器能减小主体结构在不同动力作用下（包括自由振动，实际地震波激励和白噪声激励）的均方根加速度响应。选用合适的填充率对调谐颗粒阻尼器的减振效果影响最大。填充率与衰减率的关系曲线具有两个峰值，当填充率处于这两个峰值附近时更可能达到较高的衰减率。当填充率固定，改变颗粒的质量对衰减率影响不大，这说明实际使用中只要满足一定填充率，可以使用较轻的材料代替较重的材料。地震波输入的能量与振动衰减率并不呈现线性关系。地震波频率特性对衰减率也有影响，当地震波能量谱集中在结构自振频率附近时，结构衰减率较高。总体来说，调谐颗粒质量这一新型阻尼器能够有效减小主体结构在动力作用下的响应，具有在土木工程应用的良好前景。

［1］李晓玮，施卫星．人行天桥MTMD减振控制的鲁棒性研究［J］．结构工程师，2012，28（4）：7－12．

LI Xiao-wei，SHI Wei-xing．Research on robustness of vibration control of pedestrian bridges using multi degree of freedom passive tuned mass-dampers［J］．Structure Engineers，2012，28（4）：7－12．

［2］鲁正，吕西林．缓冲型颗粒阻尼器减振控制的试验研究［J］．土木工程学报，2013，46（5）：1－6．

LU Zheng，LÜXi-lin．Experimental investigation into the vibration control effects of buffered particle dampers［J］．China Civil Engineering Journal，2013，46（5）：1－6．

［3］闫维明，黄韵文，何浩祥，等．颗粒阻尼技术及其在土木工程中的应用展望［J］．世界地震工程，2010，26（4）：18－24．

YAN Wei-ming，HUANG Yun-wen，HE Hao-xiang，et al．Particle damping technology and its application prospect in civil engineering［J］．World Earthquake Engineering，2010，26（4）：18－24．

［4］Eren Semercigil S，Collette F，Huynh D．Experiments with tuned absorber-impact damper combination［J］．Journal of Sound and Vibration，2002，256（1），179－188．

［5］ZhiWei-xu，Chan KW，Liao W H．An empiricalmethod for particle damping design［J］．Shock and Vibration，2004，11：647－664．

［6］Papalou A，Masri S F．Response of impact dampers with granular materials under random excitation［J］．Earquake Engineering and Structural Dynamics，1996，25：253－267．

［7］李创第，黄天立，李暾，等．TMD控制优化设计及振动台试验研究［J］．土木工程学报，2006，39（7）：19－25．

LIChuang-di，HUANG Tian-li，LITun，et al．Optimal TMD design and shaking table test［J］．China Civil Ebgineering Journal，2006，39（7）：19－25．

［8］鲁正，吕西林，闫维明．颗粒阻尼器减震控制的试验研究［J］．土木工程学报，2012，45（S1）：243－247．

LU Zheng，LÜXi-lin，YAN Wei-ming．Experimental investigation into the vibration control effects of particle dampers［J］．China Civil Engineering Journal，2012，45（S1）：243－247．

Experimental study on a new type of tuned mass dam per

SHIWei-xing1，HE Bin1，LIXiao-wei2，LU Zheng1
（1．Research Institute of Structural Engineering and Disaster Reduction，Tongji University，Shanghai200092，China；2．Tongji Architectural Design（Group）Co．，Ltd．，Shanghai200092，China）

A new type of tunedmass damperwas generated by taking advantage of a box filled with particles instead of solid mass．The vibration reduction effectswith orwithout this new damper under free vibration，white noise stimulation and onsite earthquake excitations were investigated by a series of shaking table tests．A bent frame with single degree of freedom was selected as themain structure in the experiments．It is shown that the filling ratio of particles has a significant influence on the vibration control，revealing the characteristics of bimodal curve；lightweightmaterials could be applied in practice owing to the slight effect of the particle mass on vibration reduction；a parabolic curve reveals the relationship between the input energy of seismic waves and the vibration damping．Also，the tests verify the effective vibration reduction performance of the new type of tuned mass damper from the aspect of vibration mode control．

new type of tuned mass damper；shaking table test；structural vibration control；influential factor

TU352；TB535

A

10．13465／j．cnki．jvs．2015．12．035

2013－05－23 修改稿收到日期：2014－05－29

施卫星 男，博士，教授，1962年生

邮箱：swxtgk＠tongji．edu．cn