含植物明渠流动分区和特征尺度研究进展

闫 静，陈 扬，唐洪武，戴 坤，张 明

（1.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学 水利水电学院，江苏 南京 210098）

含植物明渠流动分区和特征尺度研究进展

闫 静1，2，陈 扬2，唐洪武1，2，戴 坤2，张 明2

（1.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学 水利水电学院，江苏 南京 210098）

植物是生态河流必不可少的要素之一。植物的存在，改变了水流的紊流结构。由于流动沿垂向具有较强的不均匀性，对于含植物明渠紊流统计特性的描述，至今未有公认的、统一的沿水深分布表达形式。因此，对含植物明渠流动分区和各区特征尺度的研究越来越受到重视。本文回顾了无植物明渠和含植物明渠流动分区及特征尺度研究的主要成果，重点对基于流速分布和紊流结构两种方法确定的分区和特征尺度进行了分析和总结。指出将涡结构与流动特性参数分布规律相结合进行流动分区，在各区确定合适的特征尺度，进一步探究分区界限及流动特征尺度的影响因素及具体影响，建立普适的紊流统计特性分布规律是今后含植物明渠紊流结构研究的重要内容和趋势。

含植物明渠；紊流结构；流动分区；流动类型；流动特征尺度

1 研究背景

植物作为河流生态系统的重要组成部分，具有不可替代的作用［1］。宏观上，植物的存在有利于减缓水土流失，稳固岸坡和边滩。微观上，植物不仅能够直接吸收包括氮磷等植物性营养物在内的污染物，而且可以通过改变微生物环境，促进污染物的氧化分解，给生物提供养分，提高河流的自净能力［2-3］。为了实现水环境、水生态的可持续发展，越来越多的河流管理和生态修复工作者们认识到了植物在河流中的重要性，倡导建设含植物的生态河道。

由于植物粗糙元的特殊性，与传统无植物明渠水流相比，含植物明渠的流动特性和紊流结构发生了显著变化，传统光滑明渠紊流理论不能直接应用于含植物明渠水流中。明渠紊流基本统计特性参量如平均流速（流速一阶矩）、紊动强度（流速二阶矩）、雷诺应力（流速二阶矩）、偏态系数（流速三阶矩）、峰态系数（流速四阶矩）的分布，是刻画紊流结构的基础。早在1993年，Nezu等［4］就总结了光滑明渠的经典流速对数分布律、紊动强度指数分布律、雷诺应力的线性分布律，这些结论得到公认，各种光滑明渠流动，其紊流统计参量分布形式一致、参数几乎为同一常数（如流速对数分布律中卡门常数约为0.4，积分常数约为5.5；紊动强度的指数分布中，经验常数大致为固定值）。而研究发现，在植物条件下的明渠中，即使是对于简单的流速一阶统计矩—平均流速分布，都不存在统一的普适表达形式。

研究者认为是由于植物种类、密度、刚度、几何形状、淹没度、水流强度不同，才导致了流动参量分布形式的不同［5-8］。但是随着研究的深入，笔者发现其本质原因：没有选取合适的、涵盖了上述诸多因素的流动特征尺度，即长度尺度（length scale）和速度尺度（velocity scale）（尺度也称为比尺［9］，为了和物理模型上的“比尺”区分，本文统一定义为尺度），来对流动参数进行有效的无量纲化，因此无法得到公认的、统一的流动参数分布规律。

植物条件下的明渠流动沿垂向存在较强的不均匀性，流动特征尺度沿水深应有较大差异。因此，需要对流动进行分区，在不同的流动区域，为长度和速度选择相应的流动尺度，借助这些合适的特征尺度将紊动特征量进行有效的无量纲化，进而得到普适规律。

2 明渠流动分区和特征尺度研究

2.1 经典分区和尺度对于光滑明渠紊流，流动特征尺度的研究比较成熟。光滑明渠流动沿水深自床面向自由表面可以分为3个区域：

近壁区域，y＜（0.15～0.2）H，y为距床面距离，H为水深。这一区域对应于经典边界层理论分析中的内层，包括黏性底层、过渡层和对数区，其长度和速度尺度分别是黏性长度ν/u*和摩阻流速u*。

中间层，0.2 H＜y＜0.6 H。长度尺度和速度尺度分别为y和u*。

自由水面区，0.6 H＜y＜H。长度尺度和速度尺度分别为水深H和最大纵向流速Umax。

在近壁区，纵向平均流速U分布服从壁面定律（the law of the wall），无量纲化流速U＋＝U/u*与无量纲化长度y＋＝y u*/ν，在黏性底层为线性关系，在对数区满足对数分布。

Keulegan提出在明渠流动中可以假定沿全水深满足对数流速分布，这一假定在实际中一直得到应用。但20世纪80年代的研究表明，经典的标准对数分布律只在壁面层内成立，实测流速分布与对数分布公式之间的差别不应通过调整常数来消除，而是必须加入尾流函数，因此外区（中间层与自由水面区）的流速分布公式为对数－尾流定律（log-wake law）［4，9］。

对于高阶紊流统计特性，如紊动强度和雷诺应力，一般采用H和u*作为尺度，前者得到了半理论的指数分布律，后者得到了经验的线性分布律。偏态系数和峰态系数，根据定义，本身为无量纲参量，在描述其分布规律时，一般采用黏性长度作为长度尺度刻画其沿水深的分布［10］。

在粗糙床面明渠流动中，流速分布的长度尺度和速度尺度分别为表观糙率［9］（与粗糙高度ks、黏性底层计算厚度δv、Einstein校正系数χ有关）和摩阻流速u*。紊动强度和雷诺应力分布的尺度与光滑明渠相同。

2.2 其他尺度Zagarola等（1998）［11］类比管流研究，采用边界层厚度δb作为长度尺度，U∞δ*/δb（其中U∞为自由表面水流流速，δ*为位移厚度）作为速度尺度，对外区流速分布进行无量纲化，与采用u*和U∞作为速度尺度进行了对比研究，实验数据分析表明使用新的特征尺度对流速分布进行无量纲化，数据曲线更为集中。同时，他采用传统的黏性长度和摩阻流速作为尺度，研究了叠加区（overlap region，黏性底层之上、边界层厚度以内的区域）的流速分布，认为雷诺数较大时，流速分布仍符合对数律，而雷诺数较小时，流速分布更符合幂律。Cheng（2007）［12］采用内区的高度和内区上边界处的流速作为特征尺度，认为流速较好的符合幂律分布，适用的水深范围更大，且幂指数可以表达为雷诺数、水动力粗糙高度的函数。这些研究表明雷诺数对流速分布律具有影响。

3 含植物明渠流动分区和特征尺度研究

植物非淹没条件下，各阶紊流统计特性沿水深分布近似为常数，平均流速可以表达为流量、过水断面及植物分布密度的函数（闫静，2008）［13］。

植物淹没条件下，流动分区一般基于流速分布基础之上，基于紊流结构对流动进行分区的研究近几年开始发展起来。流动特征尺度的研究处于探索阶段，研究者一般类比有砂砾床面明渠流动，进行经验性或半经验性的研究。

3.1 基于流速分布的流动分区和特征尺度研究对同一实验条件下的流速，采用不同的特征尺度进行无量纲化，往往得到的分布规律差异很大［14］，且不同的无量纲化尺度具有不同的适用条件［15］。流经淹没植物的水流，一个明显的特征是纵向流速沿水深分布在植物顶端附近出现拐点，并存在流速分区现象，很难用统一的公式对整个水深的流速分布规律进行描述。基于流速分布特点，国内外学者对流速的划分存在两区和三区的观点。

3.1.1 流速的两区划分及特征尺度 支持两区划分的学者大都将流速分布分为植物层内部和植物层上部两个区域。Kouwen等［16］采用植物高度Hv作为长度尺度，传统摩阻流速u*作为速度尺度；Stephan等［17］将植物床面类比为沙粒床面，采用植物弯曲后的平均高度Hiv作为长度尺度，u*作为速度尺度，两者均认为植物层上部流速分布符合对数律，并提出了相应的对数分布公式。部分学者也基于粗糙床面明渠流动类比，采用其他尺度，得到了植物层上部流速的不同对数分布律［18-20］。

有学者基于掺混长度理论或类比混合层理论，对流速分布进行了研究。槐文信等［21］将理论分析和水槽实验相结合，采用Hiv为长度尺度，植物层顶部的摩阻流速其中S为水槽坡度）（Järvelä提出［22］）作为速度尺度，提出了基于掺混长度理论的适用于植物层上部的流速分布公式。Cheng等［14］对淹没度≤2的刚性植物淹没水流进行研究，类比平面混合层，从理论上提出一种新的长度尺度—半厚度y1/2（流速为（Umax-Uv）/2处至自由水面的距离，Uv是植物顶部处流速），采用Umax-Uv作为速度尺度，对植物层上部的流速进行无量纲化，与对数律、幂律、流速亏损律相比，效果较好。基于流速确定的两区划分及特征尺度见图1。

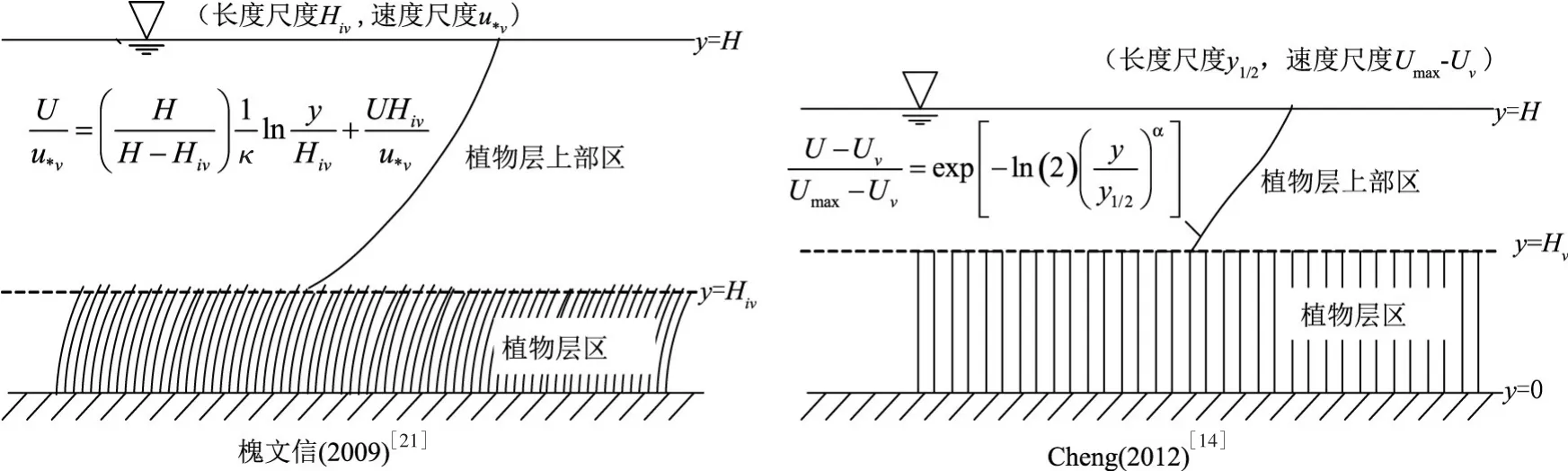
图1 基于流速两区划分及特征尺度

3.1.2 流速的三区划分及特征尺度 与两区相比，对三区划分的各区边界位置与各区遵循的流速分布律并未达到统一［5］。

Gourlay［23］采用天然柔性植物进行水槽实验，根据流速测量数据，将含淹没植物水流沿垂线分为三个区域：区域1（0＜y≤k）（k为流速分布满足对数律的起点位置），即近床面植物层底部，流速较小、为一常数，且与传统摩阻流速成正比；区域2（k＜y≤Hiv），流速沿水深符合对数分布；区域3（Hiv＜y≤H），流速符合另一对数分布。他并未对流速分布的长度和速度尺度进行研究。同时，他指出底坡对流速分布具有影响：当底坡大于0.05时，第二区和第三区合并为一个区域。

Ei-Haikim等［24］用带有枝杈的塑料条模拟天然植物，在梯形水槽中进行实验，将流动沿水深分为3个区域：区域1（0＜y≤Hiv），以Hiv和Uv作为特征尺度，流速分布符合幂律；区域2（Hiv＜y≤Hv1，Hv1为略高于植物顶部的一个高度），流速符合线性分布；区域3（Hv1＜y≤H），此区域流动与植物糙元无关，当以H和Umax作为特征尺度时，流速分布符合幂律；当以Hiv和u*或ν/u*和u*作为特征尺度时，流速分布符合对数律。

Carollo等［25］利用ADV测量含淹没柔性植物水流垂线上纵向流速分布，提出以Y1和Y2为界限的三区划分（其中Y定义为y/H（垂向位置/水深），Y1和Y2分别位于植物顶端上方和下方），并以水深H为长度尺度，传统摩阻流速u*为速度尺度，结合混合长度理论和测量数据结果，得出反正切函数速度分布形式。

Shi等［26］根据柔性植物水槽实验测得的流速分布曲线，将流动分为三个区域，他们认为摩阻流速在植物层内部，不是一个合适的速度尺度，而上层流动需要摩阻流速作为速度尺度，并总结了各种计算摩阻流速的方法：重力法，对数分布法，近床面雷诺应力法，紊动能法等。

此外，闫静［13，15］总结和讨论了6种速度尺度的计算方法和适用条件，在研究流速分布时，选取了综合摩阻流速其中R′为考虑植物的综合水力半径），并采用H、Hv和ν/u*分别作为长度尺度，对流速分布沿整个水深进行无量纲化，结果表明流速分布规律互为相似，但分布曲线互不重合，即为无效的普适无量纲化。

3.2 高阶紊流统计特性的流动尺度研究López［27］使用Hv为长度尺度，尝试将4种植物顶端处物理量（流速Uv，纵向紊动强度垂向紊动强度用雷诺应力计算的作为相应物理量的速度尺度。该类尺度以植物顶部处的物理量作为参照，所有工况下不同无量纲物理量在y/Hv＝1处重合于一点，能够清楚的反映各物理量在植物内层和上方区域与植物顶部处之间的偏离程度，但对于得到普适的分布规律意义不大。

闫静［13］分别采用H和Hv作为长度尺度，最大雷诺应力计算的摩阻流速为速度尺度，对紊动强度和雷诺应力分布进行无量纲化，研究发现，各种实验工况下，采用H作长度尺度时，植物层上部实验数据较为集中，而植物层内部数据分散；采用Hv为长度尺度时，规律恰好相反。因此分别采用Hv、H作为植物层内部和上部的长度尺度，为速度尺度，建立了紊动强度、雷诺应力分布公式。紊动强度在植物层上部和内部均符合各自特征尺度下的指数分布。淹没度较小时，雷诺应力在植物层上部符合指数分布，淹没度较大时，符合线性分布；而在植物层内部，雷诺应力近似符合指数分布。

Yang等［28］采用雷诺应力最大值处高度为长度尺度，为速度尺度，认为植物层上下紊动强度均满足不同系数的指数分布，且刚性植物比柔性植物条件下数据曲线与公式更吻合。Nikora等［29-30］对比分析了对其计算方法及物理意义进行了详细的讨论，认为后两者更适合作为高阶紊流统计特性的无量纲化尺度，这一观点和闫静［13，15］相同。

对于偏态系数和峰态系数，由于其本身为无量纲数，对于特征尺度研究仅限于长度尺度。Poggi等［31］、闫静［13］使用Hv作为长度尺度，均发现植物层内部偏态系数Sku＞0（纵向流速偏态系数），Skv＜0（垂向流速偏态系数）；植物层上部则与之相反。峰态系数Kuu和Kuv在植物顶端达到最小值，向渠底和自由水面逐渐增大，分析表明，植物顶端附近纵向流速概率密度符合正态分布。

总结前人研究成果，常见的长度尺度包括：植物高度Hv、柔性植物弯曲后的平均高度Hiv，黏性长度ν/u*，水深H等；常用的速度尺度包括：断面平均流速Um、植物顶端处物理量（流速Uv，纵向紊动强度垂向紊动强度雷诺应力计算的其他各种方法计算的摩阻流速等。但无论上述何种单一尺度，都无法使得紊流统计特性的表达统一起来。

3.3 基于紊流结构的流动分区和特征尺度研究目前分区大多基于各家得到的流速分布，因此造成了（1）分区具有特定性，即某种分区和特征尺度仅对某一研究适用；（2）无法用基于流速分区确定的特征尺度对高阶紊流统计特性进行有效的无量纲化。鉴于含植物明渠流动沿垂向较强的不均匀性和复杂性，应从紊流内部结构考虑对流动进行分区，在各区寻找合适的流动特征尺度。

Raupach等［32］对流经陆生植物的大气流动进行了研究，根据紊动能的产生项G和耗散项ε的关系，将冠层流动分为3个区域：粗糙次层（Roughness Sublayer）（床面至植物层上部某一区域，G＞ε）、惯性区（粗糙次层以上满足G≈ε的区域），自由表面区（惯性区以上区域，G＜ε）。Poggi等［31］利用水槽实验和理论分析，认为含淹没植物明渠分区与之相似，将粗糙次层定义为冠层次层（Canopy Sublayer），各区的界限尚不清楚。

Nepf团队［33-38］结合理论分析和水槽实验，对含淹没植物明渠水流进行了系列研究。他们指出植物密度对流动分区和流动类型有影响。在植物密度较小的情况下，水流为边界层流动；在植物密度较大的情况下，流动沿垂向分为3个区域：低冠层区（0≤y≤Hv-δe）、混合层区（Hv-δe＜y≤Hv-δe＋tml）、自由水面区（Hv-δe+tml＜y≤H），其中δe是KH涡渗透深度，tml是混合层厚度（KH涡的垂向尺度）［39］。对于混合层区流速分布的特征尺度，他们认为可以使用动量厚度θ（通过混合层上下边界的流速计算得到）作为长度尺度，混合层上下边界的速度差ΔUml作为速度尺度，流速可以用双曲正切函数来描述。将Tang［40］由局部紊流结构确定的植物局部阻力系数cd分布结果，与Nepf［37］的KH涡渗透深度位置进行对比，发现Hv-δe处正是cd由近似常数区变为增大区的拐点。在低冠层区，cd和雷诺应力近似保持为一常数，说明低冠层区流动和非淹没流动类似，不存在KH涡的扰动。

Nezu等人［41-43］利用象限分析和时空相关分析等紊流结构研究方法和水槽实验，将整个水深沿垂向划分为3个区域：类非淹没区（0≤y＜hp），混合层区（hp≤y＜hlog）和对数层区（hlog≤y≤H，类边界层流动），其中hp是植物层内雷诺应力为最大值10%时对应的高度，hlog约为1.7 Hv，混合层区的厚度hloghp与淹没度相关。他们也认为混合层区流速可以用双曲正切函数进行描述。基于紊流结构的流动分区见图2。

图2 基于紊流结构的三区划分

闫静等［39］将Poggi、Nepf、Nezu的研究成果进行了对比分析，总结了植物密度变化下紊流结构变化的过程：植物很稀疏条件下，植物对水流结构扰动较小，流动类型仍为壁面边界层流动，随着植物密度增大，植物影响增大，流动类型完成了从边界层到混合层的过渡，而植物密度再增大到一定程度时，极密的植物层形成了新的壁面边界，新的边界层流动形成。

戴坤等［44］利用流动显示技术，对含植物条件下明渠紊流拟序结构进行了观察和分析，将流动分为三个特征区域：植物内层区，主要表现为弱猝发现象并形成类卡门涡街，涡结构受植物直径和植物排列方式影响较大；植物顶部附近区，紊流结构复杂，表现为猝发现象和自由混合层中大涡配对现象的叠加；植物外层区，类似于传统壁面边界层外区中所表现出的顺水流方向水体拉伸以及紊流的间歇性。

4 结论与展望

综上，目前各种长度和速度尺度的确定主要基于流速分布和紊流结构。基于流速分布选取特征尺度的研究相对成熟，但具有较强的特定性，使用这些特征尺度和建立的流速与高阶紊流统计特性参数分布公式只适用特定的植物或者水流条件。基于紊流结构的流动分区，更具理论性，但目前分区界限值、各区流动类型和流动特征尺度，以及影响因素的具体影响并不是很清楚。对含植物明渠流动分区和特征尺度的研究，提出如下建议：（1）从紊流机理出发，结合流动结构的内在本质特点，综合考虑涡结构（如KH涡）沿程发展变化和流动特性参数分布规律对流动进行分区，判断各区流动类型。这是确定能综合涵盖植物和水流因素的长度和速度尺度的基础。（2）探究植物条件（植物种类、刚柔性、密度、排列方式、几何特性）和水流条件（水流强度、淹没度）等影响因素对流动分区界限的具体影响。通过综合比较分析，确定其影响权重的大小，找出主要的影响因素。（3）借鉴各区流动类型相应的尺度理论，在各区探求流速、紊动强度、雷诺应力等紊流统计特性的特征尺度，以获得普适表达式。

［1］罗朝晖.生态河道构建技术及净污效果实验研究［D］.南京：河海大学.2005.

［2］王国祥，濮培民，张胜照，等.用镶嵌组合植物群落控制湖泊饮用水源区藻类及氮污染［J］.植物资源与环境，1998，7（2）：35-41.

［3］王旭明，匡晶.水芹菜对污水净化的研究［J］.农业环境保护，1999，18（1）：34-35.

［4］Nezu I，Nakagawa H.Turbulence in open-channel flows［M］.Netherlands：Balkema Publishers，1993.

［5］唐洪武，闫静，吕升奇.河流管理中含植物水流问题研究进展［J］.水科学进展，2007，18（5）：785-792.

［6］闫静，唐洪武，田志军，等.植物对明渠流速分布影响的实验研究［J］.水利水运工程学报，2011，4：138-142.

［7］何晔.植物条件下明渠紊流特性的研究［D］.南京：河海大学，2013.

［8］Chen Yang，Yan Jing，He Ye，et al.Experimental study on flow characteristics of open-channel flow with flexible vegetation［C］//Proceedings of 2014 International Conference on Mechanics and Civil Engineering.Wuhan：Atlantis Press，2014，428-432.

［9］王兴奎，邵学军，李丹勋.河流动力学基础［M］.北京：中国水利水电出版社，2002.

［10］章梓雄，董增南.粘性流体力学［M］.北京：清华大学出版社，1998.

［11］Zagarola M V，Smits A J.A new mean velocity scaling for turbulent boundary layers［C］//1998 ASME Fluids Engineering Division Summer Meeting.Washington DC：1998.

［12］Cheng N S.Power-law index for velocity profiles in open channel flows［J］.Advances in Water Resources，2007，30：1775-1784.

［13］闫静.含植物明渠水流阻力及紊流特性的实验研究［D］.南京：河海大学.2008.

［14］Cheng N S，Nguyen-H T，Tan S K，et al.Scaling of velocity profiles for depth-limited open channel flows over simulated rigid vegetation［J］.Journal of Hydraulic Engineering，2012，138（8）：673-683.

［15］闫静，唐洪武，田志军，等.淹没植物条件下的明渠流速比尺研究［ED/OL］.北京：中国科技论文在线［2012-02-16］.http：//www.paper.edu.cn/releasepaper/content/201202-500.

［16］Kouwen N，Unny T E，Hill H M.Flow retardance in vegetated channels［J］.Journal of the Irrigation and Drainage Division，1969，95（IR2）：329-342.

［17］Stephan U，Gutknecht D.Hydraulic resistance of submerged flexible vegetation［J］.Journal of Hydrology，2002，269：27-43.

［18］Christensen B A.Open channel and sheet flow over flexible roughness［C］//21st IHAR Congress，Melbourne：1985，462-467.

［19］Murota A，Fukuhara T，Sato M.Turbulence structure in vegetated open channel flows［J］.Journal of Hydroscience and Hydraulic Engineering，1984，2（1）：47-61.

［20］Temple D.Velocity distribution coefficients for grass-lined channels［J］.Journal of Hydraulic Engineering，1986，112（3）：193-205.

［21］槐文信，韩杰，曾玉红，等.基于掺长理论的淹没柔性植被水流流速分布研究［J］.应用数学和力学，2009，30（3）：325-332.

［22］Järvelä J.Effect of submerged flexible vegetation on flow structure and resistance［J］.Journal of Hydrology，2005，307（1）：233-241.

［23］Gourlay M R.Discussion of‘Flow resistance in vegetated channels’by Kouwen et al，［J］.Journal of the Irrigation and Drainage Division，1970，96（IR3）：351-357.

［24］Ei-hakim O，Salama M M.Velocity distribution inside and above branched flexible roughness［J］.Journal of the Irrigation and Drainage Engineering，1992，118（6）：914-927.

［25］Carollo F G，Ferro V，Termini D.Flow velocity measurements in vegetated channels［J］.Journal of Hydraulic Engineering，2002，128（7）：664-673.

［26］Shi Z J，Li Yanhong，et al.Hydrological characteristics of vegetated river flows：a laboratory flume study［J］.Hydrological Sciences Journal，2013，58（5）：1047-1058.

［27］López F.Open-channel flow with roughness elements of different spanwise aspect ratios：turbulence structure and numerical modeling［D］.Urbana-Champaign：University of Illinois.1997.

［28］Yang W J and Choi S U.Mean and turbulence structures of open-channel flows with submerged vegetation［C］// 16th Asia and Pacific Division Congress of the International Association of Hydraulic Engineering and Research& 3rd IAHR International Symposium on Hydraulic Structures，Springer Berlin Heidelberg，2008：20-23.

［29］Nikora N，Nikora V.Flow penetration into the canopy of the submerged vegetation：definitions and quantitative estimates［C］//International Conference on Fluvial Hydraulics（River Flow2010），2010：8-10.

［30］Nikora N，Nikora V，O Donoghue T.Velocity profiles in vegetated open-channel flows：combined effects of multiple mechanisms［J］.Journal of Hydraulic Engineering，2013，139：1021-1032.

［31］Poggi D，Porporato A，Ridolfi L.The effect of vegetation density on canopy sub-layer turbulence［J］.Boundary-Layer Meteorology，2004，111：565-587.

［32］Raupach M R，Antonia R A，Rajagopalan S.Rough-wall turbulent boundary layers［J］.Applied Mechanics Review，1991，44（1）：1-25.

［33］Nepf H M，Vivoni E R.Flow structure in depth-limited，vegetated flow［J］.Journal of Geophysical Research，2000，105（C12）：28547-28557.

［34］Ghisalberti M，Nepf H M.Mixing layers and coherent structures in vegetated aquatic flows［J］.Journal of Geophysical Research，2002，107：3-11.

［35］Ghisalberti M，Nepf H M.The limited growth of vegetated shear layers［J］.Water Resources Research，2004，40：W07502.

［36］Luhar M，Rominger J，Nepf H.Interaction between flow，transport and vegetation spatial structure［J］.Environmental Fluid Mechanics，2008，8：423-439.

［37］Nepf H M，Ghisalberti M.Flow and transport in channels with submerged vegetation［J］.Acta Geophysica，2008，56（3）：753-777.

［38］Nepf H M.Flow in aquatic vegetation［J］.Annual Review of Fluid Mechanics，2012，44：123-142.

［39］闫静，戴坤，唐洪武，等.含植物河道紊流结构研究进展［J］.水科学进展，2014，25（6）：926－933.

［40］Tang Hongwu，Tian Zhijun，Yan Jing，et al.Determining drag coefficients and their application in modelling of turbulent flow with submerged vegetation［J］.Advances in Water Resources，2014，69：134-145.

［41］Nezu I，Sanjou M.Turburence structure and coherent motion in vegetated canopy open-channel flows［J］.Journal of Hydro-environment Research，2008，2（2）：62-90.

［42］Nezu I，Okamoto T.Effect of vegetation density on coherent structure on turbulence in flexible vegetated openchannel flows［C］//33rd IAHR Congress，2010：5615-5619.

［43］Okamoto T，Nezu I.Spatial evolution of coherent motions in finite-length vegetation patch flow［J］.Environmental Fluid Mechanics，2013，13：417-434.

［44］Dai Kun，Yan Jing，Chen Yang，et al.Application of flow visualization and image processing techniques to the study of coherent structure in vegetated canopy open-channel flows［C］//2015 International Conference on Testing and Measurement：Techniques and Applications，CRC Press，2015.

Advances in research on sub-division and characteristic scales of open channel flows with vegetation

YAN Jing1，2，CHEN Yang2，TANG Hongwu1，2，DAI Kun2，ZHANG Ming2
（1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Nanjing 210098，China；2.College of Water Conservancy and Hydropower，Hohai University，Nanjing 210098，China）

Vegetation is an essential element in most natural ecological rivers.Its biological characteristics change turbulent structures of the river significantly.Due to the strong inhomogeneity of flow in the vertical direction，there still are no universal expressions of the turbulent statistical properties along water depth in vegetated open-channel flows.Therefore，flow sub-division and corresponding characteristic scales of these regions have gained more focuses.In this paper，the research achievements of sub-division and characteristic scales are reviewed in terms of traditional and vegetated open-channel flows.The results based on the velocity distribution and turbulent structures are analyzed and summarized respectively.The paper proposes that to partition the flow into different sub-regions by combining the vortex structure with the distribution of flow characteristic parameters，determine the appropriate characteristic scales of each sub-regions and investigate the influence factors of sub-division and characteristic scales are the main research contents and tendencies.

open channel flow with vegetation； turbulence structure； flow sub-division； flow regime；characteristic scales of flow

TV131.2；G353.11

A

10.13244/j.cnki.jiwhr.2015.06.005

1672-3031（2015）06-0428-08

（责任编辑：韩 昆）

2015-05-19

国家自然科学基金资助项目（51125034，51579079，51239003，51109066）；重大科学仪器设备开发专项（2011YQ070055）

闫静（1980-），女，新疆石河子人，博士，副教授，主要从事明渠紊流力学及河流动力学研究。E-mail：yanjing@hhu.edu.cn

唐洪武（1966-），男，江苏盐城人，博士，教授，主要从事水力学及河流动力学研究。E-mail：thwhongwu@163.com