基于改进监督LLE算法的故障特征提取方法
胡 峰,王传桐,吴雨川,范良志,余联庆
(武汉纺织大学机械工程与自动化学院,武汉 430074)
基于改进监督LLE算法的故障特征提取方法
胡 峰,王传桐,吴雨川,范良志,余联庆
(武汉纺织大学机械工程与自动化学院,武汉 430074)
针对现有监督局部线性嵌入算法在低维输出向量重构过程中监督学习能力弱,不利于故障特征提取的问题,通过利用训练样本类标签信息扩大不同类样本间平均距离的方式,增加低维输出向量重构模型的监督学习能力,强化同类样本的聚集性和异类样本的互斥性。基于规范切割准则和低维输出向量重构误差,应用离散粒子群优化算法优化折中系数α和β、以及嵌入维数和邻域等参数,提高故障特征提取精度。将改进的监督局部线性嵌入方法应用于轴承故障特征提取,结果表明推荐方法的特征提取精度较高。
故障;特征提取;监督局部线形嵌入;局部几何结构;规范切割
高维度、非线性和强耦合的机械故障信号会严重影响机械故障的诊断正确率[1-2]。监督局部线性嵌入算法(Supervised Locally Linear Embedding,SLLE)通过调节样本间的局部邻域结构实现监督学习,能强化同类样本的聚集性和异类样本的互斥性,实现故障特征流形的解耦与分类及新增样本的增量处理,提高故障辨识精度和计算效率[3-6]。但是,现有SLLE方法存在:①低维输出向量在重构过程中监督学习能力弱;②参数优化能力不足等问题。导致SLLE对故障特征提取精度差。针对上述问题,需要对SLLE进行改进。
1 SLLE算法
SLLE根据类标签寻找每个训练样本xi∈X的k个同类邻近点,采用放大异类样本间欧式距离,保持同类样本间距离不变的方法来拉大异类样本之间的距离,用公式[3-7]
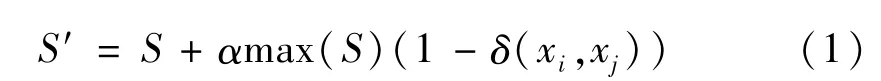
将不同类样本分别映射到低维空间,保证邻域中同类点占多数的状态。其中S=‖xi-xj‖为未考虑类标签信息时的欧式距离,max(S)=maxi,j‖xi-xj‖为样本间的最大距离,S′为融入类标签信息的距离。若xi和xj属于异类,则δ(xi,xj)=0;否则,δ(xi,xj)=1。α∈[0,1]为折中系数,用于控制类信息的融入程度。
采用式(1)构造训练样本集中每个样本点xi的k个最近邻点集合,运用
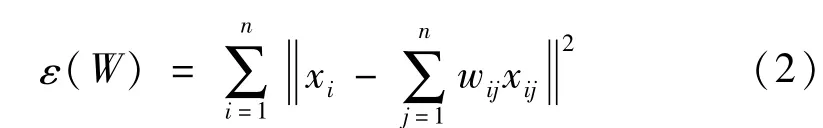
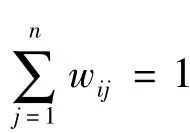
为使输出向量yi在低维空间尽量保持高维空间的拓扑结构,代价函数[8]
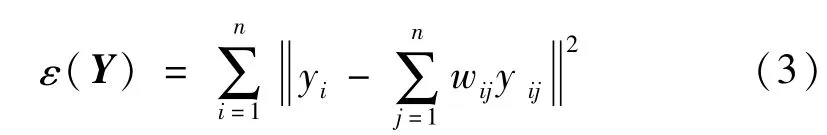
必须最小。yi是矩阵Y的列向量;式中yij(j=1,2,…,k)是yi在嵌入空间的k邻近点。且必须满足
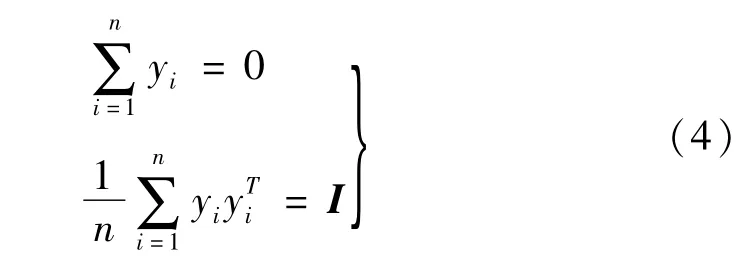
式中I是单位矩阵。在计算式(3)的最优解时,ε(Y)可写成[8]
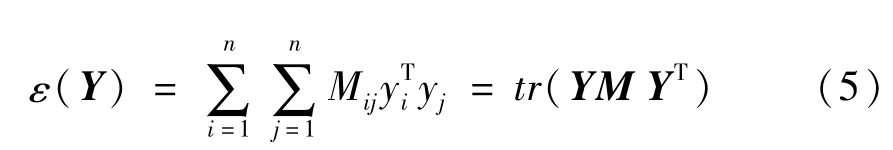
式中M是一个n×n的对称矩阵,其表达式[8]为
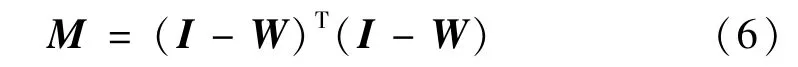
式(3)最小解为矩阵M的d个最小特征值所对应的特征向量构成的矩阵Y,则Y的列向量维数为d。
2 改进低维输出向量重构模型
针对现有SLLE方法在低维输出向量重构过程中监督学习能力不足的问题,利用训练样本类标签信息扩大不同类样本之间平均距离的方式构造监督学习机制,增强SLLE的特征提取精度。

图1 改进SLLE监督学习原理示意图Fig.1 Learningmechanism of improved supervised locally linear embedding algorithm


式(3)与式(10)具有相同表达形式。通过最小化两式的和,求取低维输出向量。但是,两式目标值大小和数量级存在差异,故设立折中系数β进行协调。


式中φ(y,β)最小时,即式(3)与式(10)两式分别最小时,获得的低维输出向量y即为所求。式(12)进一步改写为

3 改进新样本特征提取方法
设新样本为xnew,它在训练样本集中的k个最近邻点为xj,j=1,2,…,k。yj为xj的低维输出向量。令X=[xi,x2,…,xk],Y=[y1,y2,…,yk]。现有SLLE方法利用公式[3-4,9]:

计算映射矩阵A。然后通过矩阵A计算新样本的低维输出向量。但是,当XT为不满秩矩阵时,如:邻近点数目k小于高维空间维数D时,矩阵A计算困难。
LLE方法必须满足两个前提假设:在高维空间满足[8]
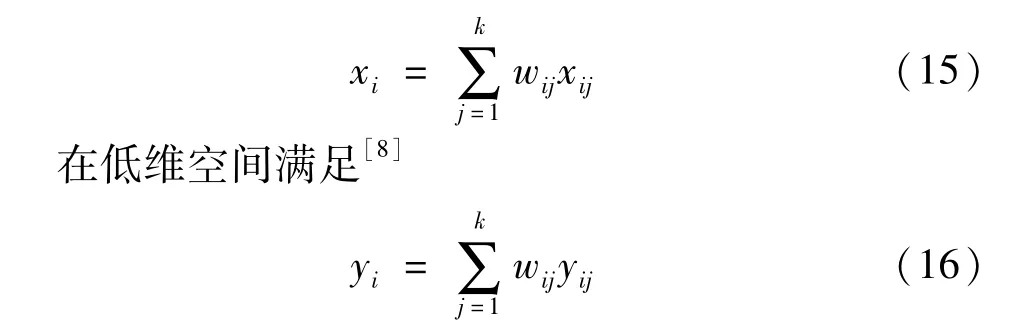
本文推荐的方法是先找出新样本在训练样本集中的k个邻近点xj,j=1,…,k,计算xnew和xj间的权值wij。由于yj已经利用改进SLLE计算得到,使用式(16)可计算出ynew,注意使用式(16)时,要求重构误差较小。
4 改进SLLE参数的优化方法
式(1)和式(13)中的折中系数α和β,以及嵌入维数d和邻域大小k都会影响故障特征的提取精度[10],需要进行优化。
4.1 改进SLLE参数的优化准则

本文推荐采用规范切割(简称Ncut)准则和重构误差作为参数优化准则。Ncut准则能用于衡量类可分性的优劣。设样本点能划分为K类,Ci是属于类i的样本点集合,则Ncut准则[11-13]为
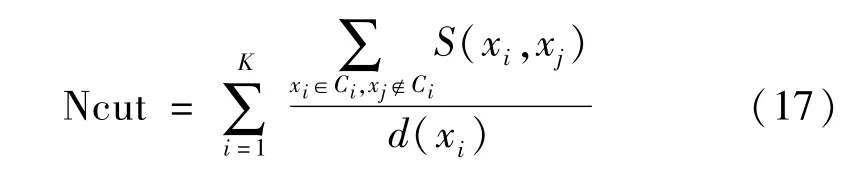

式中d(xi,xj)是顶点xi和xj间的欧式距离,σi(σj)是顶点xi(xj)与邻域点的平均距离。如果边(xi,xj)∉E,则S=0。由式(18)可知S∈[0,1],使不同维度空间计算得到的边权值具有可比性,进一步使衡量类可分性的Ncut值在不同子空间具有可比性。
新样本通过式(16)提取故障特征,为了使新样本具有较高的故障特征提取精度,式(3)中重构误差ε越小越好。
4.2 基于离散粒子群的参数优化算法


式中:i=1,2,…,L,j=1,2,…,N;r1j,r2j和ρ是[0,1]上均匀分布的随机数;ω,c1和c2是权重及加速度系数。
基于离散粒子群的参数优化算法如下:
步骤1 初始化粒子群参数。设置种群大小、粒子维数;
步骤2 计算每个粒子适应度值。将二值粒子转化为十进制参数值,利用改进SLLE算法计算训练样本的低维输出向量。将式(3)和式(17)同时作为适应度函数,分别计算两式的值。步骤3 计算个体适应度最好位置第t+1次迭代后,粒子xi(t+1)的适应度值比它历史最好位置的适应度值小时,即:目前计算得到的重构误差和Ncut值同时小于或等于历史最好位置的重构误差和Ncut值的情况下,更新粒子xi的历史最好位置xpi。
步骤4 计算全局最好位置。利用全局最好位置计算得到的重构误差和Ncut值要同时小于或等于个体最好位置的重构误差和Ncut值。
步骤5 利用式(18)~式(20)更新粒子速度和位置。
步骤6 检测是否达到终止条件。如果达到则停止,否则返回步骤2。
5 实验研究
5.1 实验目的和方法
在相同条件下,与现有方法进行对比实验研究,证明改进SLLE方法提取的故障特征向量灵敏度更高;特征向量维数更小。
对比实验中涉及的方法有:①改进SLLE方法。该方法在轴承故障特征提取中同时应用重构误差和Ncut准则作为适应度函数,应用离散粒子群算法优化折中系数α和β、以及嵌入维数和邻域大小,应用式(16)提取新样本故障特征。②SLLE方法[3-4]。该方法在轴承特征提取过程中应用局部协方差矩阵的特征值来确定嵌入维数,用十折交叉验证法确定邻域大小和折中系数α,应用式(14)提取新样本的故障特征。③LLE方法和基于相关熵的局部线形嵌入算法(CCLLE)[13]。两种方法在轴承故障特征提取中应用Ncut准则优化嵌入维数和邻域大小,应用式(16)提取新样本故障特征。
5.2 实验数据来源
实验数据来源和原始特征集的构造方法与文献[13]相同。选择美国Case Western Reserve University电气工程实验室提供的SKF6205型深沟球轴承在正常和不同故障状态下的振动信号数据进行分析研究。从轴承振动信号中提取波峰指标、峭度指标、偏度指标、裕度指标、标准差、均方根和峰值等7个时域特征。采用小波包函数将不同状态下的滚动轴承振动信号进行p层正交小波包分解,得到由全频带均匀划分的2p个子频带的滤波信号,将各频带信号的能量作为原始特征集[13]。原始特征集由时域特征和频域特征共同构成,共计7+2p个特征。
5.3 实验过程
在不同转数、采样频率和故障尺寸情况下,选取正常状态、滚珠故障、内圈故障和外圈故障等4种状态下的轴承振动信号。
(1)实验一
信号采样频率为48 kHz,转速1 750 r/min,故障尺寸0.036 cm,进行p=7层正交小波包分解,得到135个特征。每种状态样本数为29,样本长度为16 384,计算原始特征集。首先,在每种状态中随机选取15个样本组成训练样本集,其余作测试样本。需要特别指出:应用SLLE方法时,如果按十折交叉验证法要求,将训练样本分成10个测试子集,每个测试子集中每类样本平均只有1.5个,数量太少。为提高每个测试子集不同类样本的数量,实验中将训练样本分成5折。邻域和折中系数α的步长与文献[3-4]一致。改进SLLE算法中离散粒子群的迭代次数为400。然后,计算训练样本的低维输出向量,并将结果用于训练概率神经网络分类器;接下来,提取新样本的低维输出向量;最后,将新样本低维输出向量输入概率神经网络分类器分类。所有实验中,分类器参数不变。识别正确率和优化参数见表1。

表2 实验二结果Tab.2 Classification result of Experiment 2
(2)实验二
信号采样频率为12 kHz,转速1 730 r/min,故障尺寸0.018 cm,每种状态样本数为58,样本长度为2 048。计算原始特征集时,进行p=5层正交小波包分解,小波特征和时域特征共计39个。首先,在每种状态中随机选取40个样本组成训练样本集,其余作为验证样本。应用SLLE方法时,将训练样本分成10个测试子集。其它实验步骤和实验一相同,识别结果见表2。
5.4 实验结果分析
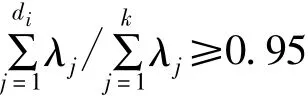
6 结 论
通过改进SLLE方法的低维输出向量重构模型、新样本的特征提取方法和参数优化方法,能提高轴承故障特征的特征提取精度,同时获得较小的维数。通过实验证明相对于局部协方差特征法和十折交叉法,Ncut准则更适合用于对嵌入维数和邻域进行优化,即使没有引入监督学习机制,Ncut准则通过有效测量低维输出向量的类可分离性,也能提高新样本的特征提取精度。同时将重构误差和Ncut值作为参数优化准则,有利于新样本特征的提取精度。
[1]栗茂林,王孙安,梁霖.利用非线性流形学习的轴承早期故障特征提取方法[J].西安交通大学学报,2010,44(5):45-49.
LIMao-lin,WANG Sun-an,LIANG Lin.Feature extraction for incipient fault diagnosis of rolling bearings based on nonlinearmanifold learnging[J].Journal of Xian Jiao Tong University,2010,44(5):45-49.
[2]张绍辉,李巍华.可变近邻参数的局部线性嵌入算法及其在轴承状态识别中的应用[J].机械工程学报,2013,49 (1):81-87.
ZHANG Shao-hui,LIWei-hua.Variable nearest neighbor locally linear embedding and applications in bearing condition recognition[J].Journal of Mechanical Engineering,2013,49 (1):81-87.
[3]李锋,田大庆,王家序,等.基于有监督增量式局部线形嵌入的故障辨识[J].振动与冲击,2013,32(23):82-88.
LI Feng,TIANG Da-qing,WANG Jia-xu,et al.Fault identification method based on supervised incremental locally linear embedding[J].Journal of Vibration and Shock,2013,32(23):82-88.
[4]Li Ben-wei,Zhang Yun.Supervised locally linear embedding projection(SLLEP)for machinery fault diagnosis[J].Mechanical systems and Signal Processing,2011,25:3125-3134.
[5]阎庆,梁栋,张晶晶.基于Fisher变换的植物叶片图像识别监督LLE算法[J].农业机械学报,2012,43(9):179-183.
YAN Qing,LIANG Dong,ZHANG Jing-jing.Recognition method of plant leaves based on fisher projection-supervised LLE algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(9):179-183.
[6]Zhao Ling-xiao,Zhang Zhen-yue.Supervised locally linear embedding with probability-based distance for classification [J].Computers and Mathematics with Applications,2009,57:919-926.
[7]Ridder D D,Kouropteva O,Okun O.Supervised locally linear embedding[C]//Proceedings of the Joint International Conference,ICANN/ICONIP.Lecture Notes in Computer Science,Springer,Heidelberg,2003:333-341.
[8]Roweis ST,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.
[9]Nichols J M,Bucholtz F,Nousain B.Automated,rapid classification of signals using locally linear embedding[J].Expert Systemswith Applications,2011,38:13472-13474.
[10]Kouropteva O,Okun O,Pietikainen M.Selection of the optimal parameter value for the locally linear embedding algorithm[C]//In:Fisrt Internat.Conf.on Fuzzy Systems and Knowledge Discovery,2002.
[11]Shi Jian-bo,Malik J.Normalized cuts and image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(8):888-905.
[12]Tabatabaei S S,Coates M,Rabbat M.GANC:Greedy agglomerative normalized cut for graph clustering[J].Pattern Recognition,2012,45:831-843.
[13]胡峰,苏讯,刘伟,等.基于改进局部线性嵌入算法的故障特征提取方法[J].振动与冲击,2015,34(15):211-215.HU Feng,SU Xun,LIUWei,et al.Fault feature extraction based on improved locally linear embedding[J].Journal of Vibration and Shock,2015,34(15):211-215.
[14]Liu Yan,Gu Xue-ping.Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization[J].IEEE Transactions on Power Systems,2007,22(3):1267-1274.
[15]Alberto G V,Rafael P.Introducing dynamic diversity into a discrete particle swarm optimization[J].Computer and Operation Research,2009,36(3):951-966.
Fault features extraction based on im proved supervised locally linear embedding
HU Feng,WANG Chuan-tong,WU Yu-chuan,FAN Liang-zhi,YU Lian-qin
(School of Mechanical Science and Automation,Wuhan Textile University,Wuhan 430074,China)
Aiming at the shortage of weak learning ability of the supervised locally linear embedding(SLLE)algorithm being unfavorable to fault feature extraction in reconstructing lower-dimensional output vectors,the learning ability of reconstructedmodel of output vectorswas improved via utilizing the information of class labels of training samples to increase the average distance between sampleswith different class labels.The aggregation of the same class samples and themutual exclusion of sampleswith different class labelswere enhanced.In order to enhance extraction precision of fault features,the binary particle swarm optimal(PSO)algorithm,the normalized cut or Ncut criterion and the reconstruction error were employed to optimize compromise coefficients,embedding dimension and neighborhood size.The improved SLLE was employed in the fault feature extraction of rolling bearings.The test results for fault diagnosis of rolling ball bearings showed that compared with other approaches,ISLLE ismore effective to extract the fault features form vibration signals,and enhance the classification ability of failure pattern.
fault;features extraction;SLLE;normalized cut criterion;PSO
TH17
A
10.13465/j.cnki.jvs.2015.21.021
国家自然科学基金资助项目(51205294,61271008,51275363)
2014-09-16 修改稿收到日期:2014-11-19
胡峰男,博士,副教授,硕士生导师,1979年生

