兆瓦级风力发电机组传动系统动态特性研究
罗勇水,周民强,陈 棋,崔 峰,刘伟江
(浙江运达风电股份有限公司,风力发电系统国家重点实验室,杭州 310012)
兆瓦级风力发电机组传动系统动态特性研究
罗勇水,周民强,陈 棋,崔 峰,刘伟江
(浙江运达风电股份有限公司,风力发电系统国家重点实验室,杭州 310012)
基于集中参数质量法建立风力发电机组四质量块柔性传动模型,在综合考虑外部风载、齿轮副啮合刚度、啮合阻尼和综合啮合误差激励条件下建立齿轮箱内部各级齿轮副动力学方程。以1.5MW风力发电机组为计算对象,计算柔性传动系统固有频率和齿轮箱各级齿轮动态啮合力,通过雨流计数法对齿轮动态啮合力进行统计分析,结果显示动态啮合力具有很强的时变特性,此研究方法为齿轮和轴承设计、寿命预估建模提供依据。并对传动系统稳定性进行分析,结果显示传动系统一阶扭振频率与风轮面内一阶摆振频率偏差为7.5%,通过降低主轴重量约8.5%,提高了传动系统一阶扭转频率值5%,提高后的频率值与风轮面内一阶摆阵频率偏差达11.9%,大于规范推荐值10%,为风力发电机组传动系统设计和可靠性研究提供参考。
风力发电;柔性传动系统;动态特性;动力学方程
目前,国内外主流的风力发电机机组为兆瓦级机组,由变桨系统、传动系统、发电系统、偏航系统、液压系统、冷却润滑系统和塔架组成,其中传动系统(桨叶、轮毂、主轴、主轴承、齿轮箱、联轴器和发电机)是吸收风能,将风能转换为旋转机械能,再将机械能转换为电能的核心系统。风力发电机组多处于环境恶劣(高海拔或海岛地形等)、变速变载、高湍流强度等复杂作业环境,传动系统是风电设备故障率高发系统[1],由于风电场地处偏远、维修困难、人员配置少、更换费用高等因素,一旦传动系统故障,将造成长时间非计划停机,严重影响机组运营,故传动系统的稳定性是风力发电机组设备可靠性运行的基石。
近年来,国外专家对齿轮箱进行了大量的研究,如:Kahraman等[2-3]建立了纯扭转振动模型,分析了齿轮箱扭转振动特性,并针对行星轮系的参数影响和稳定性进行了较深入的研究;Lin等[4]建立了行星齿轮传动系统的扭转和横向耦合振动模型,模型中将滚动轴承模拟为线性弹簧并考虑了齿轮的时变啮合刚度,分析了行星齿轮传动系统的固有频率和模态特性。国内专家、学者也开展了风力发电机组齿轮箱传动的动力学研究,如:孙涛等[5-6]建立了2K-H行星轮系弯曲-扭转耦合非线性动力学模型,采用解析谐波平衡法求解行星轮系系统的非线性频响特性;朱才朝等[7]建立了大型风力发电机组齿轮箱的多级齿轮传动系统耦合非线性动力学模型,在考虑系统内部激励的情况下对系统耦合动态特性进行了研究;王旭东等[8]通过计算风力发电机组齿轮箱在刚度激励和误差激励作用下的动态响应,获得齿轮箱的振动烈度。
目前,国际国内的研究工作侧重点为齿轮箱在内部激励条件下的动态特性研究,对行星轮系有较深入的研究,而对整个传动系统耦合状态下的动态特性研究较少,特别是在外载激励和内部激励条件下传动系统和齿轮箱的动态特性研究更少[9-11]。鉴于风力发电机组传动系统运行时动态特性,不能直接简化为刚性传动模型,仅通过分析齿轮箱动态特性代替传动系统动态特性,为了更真实、准确地描述风力发电机组传动系统在实际工况环境下的动态特性[12]。本文首先建立风力发电机组传动系统四质量块柔性模型,并建立动力学方程;在考虑外部风载、齿轮副时变啮合刚度、啮合阻尼和综合啮合误差激励条件下建立齿轮箱内部各级齿轮副啮合动力学方程。以1.5 MW风力发电机组为计算对象,计算传动系统固有频率和齿轮箱各级齿轮动态啮合力,对齿轮箱齿轮啮合力时变特性进行研究,并对传动系统稳定性进行分析,为风力发电机组传动系统设计和可靠性研究提供参考。
1 传动系统柔性传动模型
1.1 动力学模型
风力发电机组传动系统主要由桨叶、轮毂、主轴、主轴承、齿轮箱、联轴器和发电机组成,传动系统采用经典的三点支撑结构,分别由主轴承座和齿轮箱箱体两臂的弹性支撑组成,承受传动系统的倾覆和摆动力矩;风轮、主轴、齿轮箱、联轴器和发电机为传动系统转矩传递部件,也是转矩的承载部件;桨叶为风力发电机组风载吸收的部件,亦是传动系统载荷输入。
根据传动系统的结构特点,将其分解为六质量块柔性传动链模型,分别为三片桨叶等效质量块、轮毂等效质量块、齿轮箱等效质量块和发电机等效质量块组成。见图1。
式中HB1、HB2和HB3为三片桨叶等效质量块,HH为轮毂等效质量块,HGB为齿轮箱等效质量块,HG为发电机等效质量块。KBH1、KBH2、KBH3、KLS和KHS为连接部件之间的等效刚度,而连接部件之间等效阻尼系数分别用DBH1、DBH2、DBH3、DLS和DHS表示。DB1、DB2、DB3、DH、DGB和DG为各部件内部等效阻尼系数,TB1、TB2、TB3和TW分别为单片桨叶的气动转矩和总转矩,TG为发电机电磁转矩。
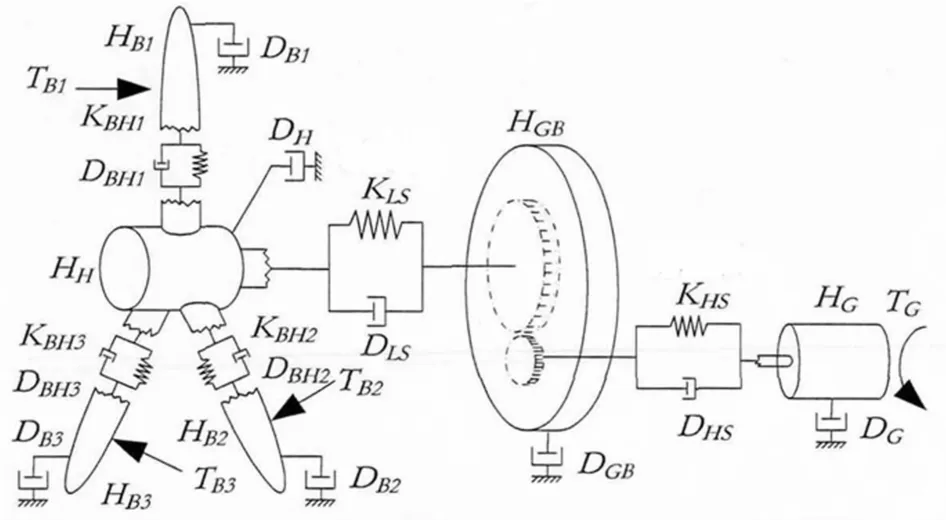
图1 传动系统六质量块模型Fig.1 Six quality blocksmodel of drive system
1.2 动力学方程
由于风力发电机组运行时,三片桨叶扫掠形成一个等效圆盘,故将三片桨叶的模型等效合成为风轮模型,六质量块传动链模型简化为四质量块传动链模型,见图2。
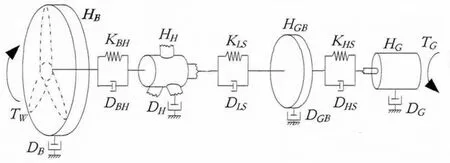
图2 传动系统四质量块模型Fig.2 Four quality blocksmodel of drive system
将HB1、HB2和HB3合成为风轮等效质量HB;KBH1、KBH2和KBH3合成为风轮等效刚度KBH;DBH1、DBH2和DBH3合称为风轮等效阻尼系数DBH;DB1、DB2和DB3合成为风轮内部等效阻尼系数DB。
建立动力学方程,如下:

式中,ωB、ωH、ωGB、ωG分别表示风轮、轮毂、齿轮箱和发电机转子的旋转角速度,ω0表示传动系统角速度基值,θBH表示风轮相对轮毂的角位移,θLS表示轮毂相对齿轮箱的角位移,θHS表示齿轮箱相对发电机转子的角位移。
2 齿轮箱传动模型
2.1 动力学模型
为了研究齿轮箱内部各级齿轮动态啮合力和轴承载荷特性,在传动系统动力学建模的基础上,考虑外部风载激励和内部激励的条件下,对齿轮箱内部传动进行动力学建模。
以额定容量1.5 MW的主流风力发电机组为计算对象,齿轮箱结构形式为一级行星二级平行轴,如图3所示,行星架c与主轴相连,为齿轮箱输入轴,将转矩通过行星级啮合传递给太阳轮s,然后由太阳轮s传递给后箱体平行级g1-g2,最后传递给g3-g4,g4为输出轴,Tin为输入转矩,Tout为输出转矩。

图3 齿轮箱传动简图Fig.3 Gearbox transmission diagram
基于集中参数质量法建立齿轮箱动力学模型,考虑各齿轮副的时变啮合刚度、轴承刚度、啮合误差和阻尼的影响,得到如图4所示。
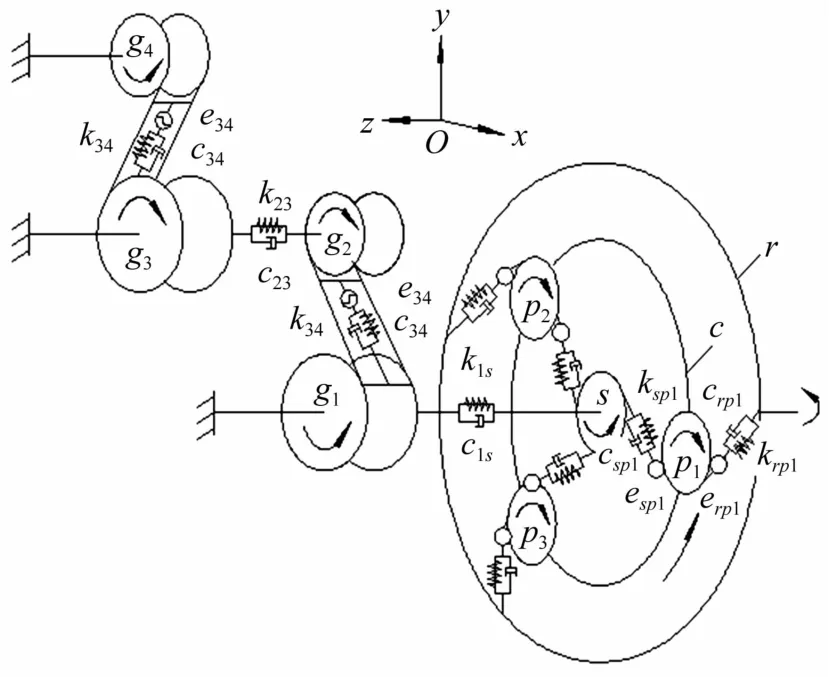
图4 齿轮箱动力学模型Fig.4 Dynamicalmodel of gearbox
太阳轮、行星架和内齿圈采用定坐标系,行星轮采用动坐标系,输入转矩作用下各构件的转动方向为角位移正向,各齿轮副啮合线位移,以齿面受压为正向。图4中,k1s、c1s为太阳轮和齿轮g1连接轴的扭转刚度和阻尼系数,k23、c23为齿轮g2、g3连接轴的扭转刚度和阻尼系数,kxy为齿轮副啮合刚度,cxy为齿轮副啮合阻尼系数,exy为综合啮合误差,(x,y)=(pi,s,r,c,1,2,3,4)。
建立齿轮箱动力学方程如下:
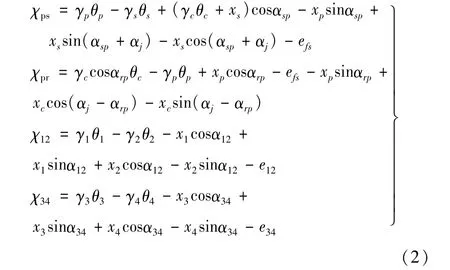
式中,xps为行星轮与太阳轮在啮合线上的变形,xpr为行星轮与内齿圈在啮合线上的变形,x12为齿轮副g1-g2在啮合线上的变形。x34为齿轮副g3-g4在啮合线上的变形。θj为各齿轮扭转角位移,αj为各旋转轴初始相位角,γj为各齿轮基圆半径,xj为各齿轮轴向振动位移,αxy为齿轮节圆啮合角。
2.2 动力学方程
通过拉格朗日方程推导出各级齿轮传动的振动微分方程,Jj、mj分别为各级齿轮转动惯量和等效质量,Fkfs、Fcfs分别为齿轮啮合副的弹性啮合力和粘性啮合力。
齿轮箱传动振动微分方程如下:

3 仿真计算
3.1 外部激励
风力发电机组的外部激励来自外界风载,风速的变化与地形、地势、地貌、海拔高度、季节性、气象等密切相关,根据IEC标准要求,使用专业风电建模软件BLADED模拟机组在额定风速附近的湍流风,并计算出传动系统输入扭矩,见图5和图6。
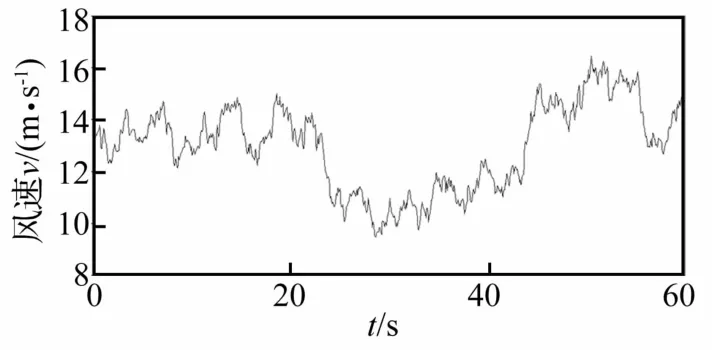
图5 外部风载Fig.5 Externalwind load
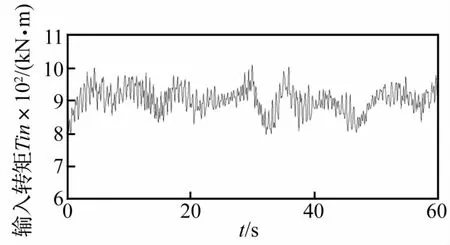
图6 传动系统输入转矩Fig.6 Input torque of the drive system
3.2 内部激励
传动系统内部激励主要来源于齿轮箱,具体为齿轮啮合的刚度激励和综合误差激励。
3.2.1 齿轮啮合的刚度激励
刚度激励是指齿轮啮合过程中啮合综合刚度的时变性引起的动态载荷,齿轮综合刚度定义为一对或几对同时啮合的齿轮在1 mm齿宽上产生1μm挠度所需的载荷,齿轮啮合综合刚度计算式如下:
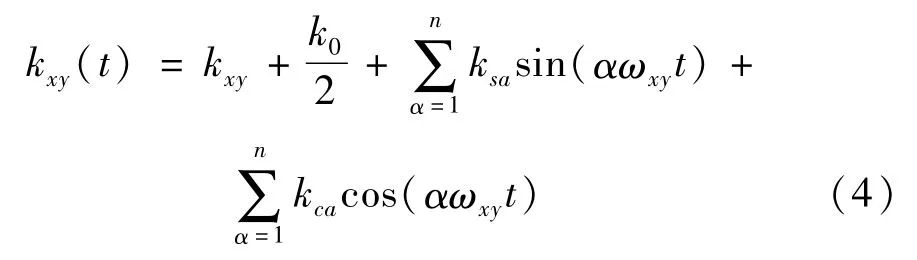
式中,ωxy为啮合频率,n为啮合刚度的谐波阶次,kxy为啮合刚度均值,ksa、kca分别为各啮合齿轮副第α阶正弦交变分量幅值和余弦交变量幅值。
根据啮合刚度公式推导出齿轮副的啮合阻尼计算公式,如下:
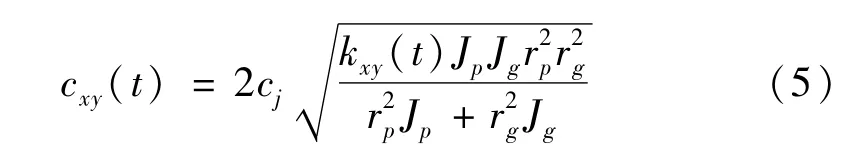
式中,cj为齿轮啮合阻尼比,根据经验一般为0.1左右,Rp、Rg分别为主、从动齿轮的基圆半径,Jp、Jg分别为主、从动齿轮的转动惯量。
3.2.2 综合啮合误差激励
齿轮啮合误差是由齿轮加工误差和安装误差引起,啮合误差使齿轮啮合齿廓偏离理论位置,使齿轮啮合状态发生变化,造成齿与齿之间的碰撞或冲击,产生了齿轮啮合的误差激励。齿轮的综合误差公式为:
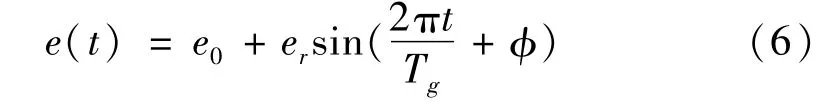
式中,e0、er分别为齿轮副综合误差的均值和幅值,Tg
为齿轮的啮合周期,φ为相位角。
3.3 动态特性计算
以额定容量1.5MW的主流风力发电机组为计算对象,主要参数:风轮直径为82 m,风轮额定转速为17.2 r/min,在标准空气密度(1.225 kg/m3)下额定风速约11.5 m/s,发电机额定转速1 800 r/min,风轮系统(除轮毂)重量约21 000 kg,轮毂和主轴重约18 000 kg,齿轮箱重量约17 000 kg,发电机重量约7 100 kg。齿轮箱增速比104.5,行星级Zr=102,Zp=40,Zs=21;平行级Z1=100,Z2=23,Z3=94,Z4=23,均为斜齿。
在外部风载激励(图6)和内部激励的作用下,计算出式(4)~(6)的齿轮副刚度、阻尼和综合误差值,将计算结果代入式(1)~(3)中,假定传动系统各部件间阻尼系数为0.05,求解传动系统动力学方程,获得传动系统固有频率和齿轮箱齿轮副动态啮合力。
传动系统前8阶固有频率如表1所示。

表1 传动系统固有频率Tab.1 The natural frequencies of the d rive system
如表1所示,系统主要阵型为:系统一阶扭振、系统上下晃动、齿轮箱行星级耦合阵型、齿轮箱低速平行级耦合阵型和齿轮箱高速平行级耦合阵型。通过对模态数据分析可知,系统低频动态响应特性主要与外部激励相关,中高频动态响应特性主要由内部激励主导。
齿轮箱内各级齿轮副动态啮合力曲线见图7。
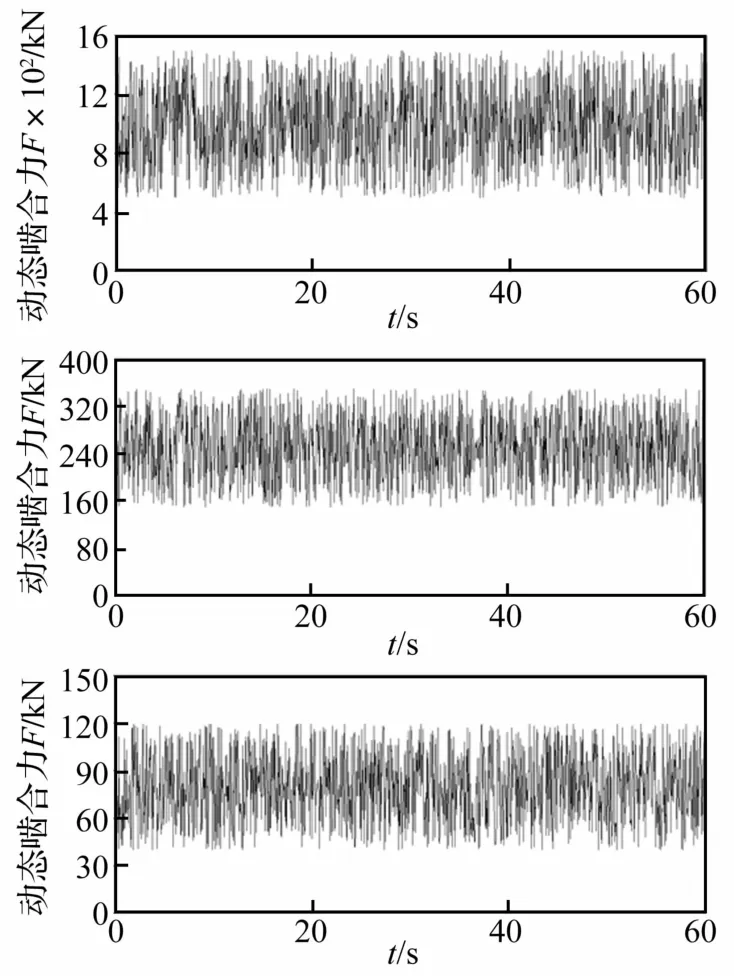
图7 齿轮箱行星级、低速平行级和高速平行级齿轮动态啮合力Fig.7 The dynamic force of gearbox planet gear、low-speed parallel gear and high-speed parallel gear
由于动态啮合力考虑了外部激励、刚度激励、阻尼和误差激励等多个因素,动态啮合力幅值波动较大,且振动频率较高,为了更好的分析动态啮合力的分布规律,以g3-g4齿轮副为例,对其动态啮合力采用雨流记数法处理,并将其转化为均值为零的幅值统计图。见图8。

图8 齿轮箱高速级齿轮动态啮合力幅值统计图Fig.8 The dynamic force statistical diagram of gearbox high-speed parallel gear
从图8可知,高速级齿轮动态啮合力幅值成正态分布,通过曲线拟合得到正态分布曲线(μ=80,σ=30),获得高速级齿轮动态啮合力的分布规律,为齿轮箱齿轮和轴承设计提供依据,并为寿命预估模型提供参考。
4 稳定性分析
根据表1结果显示,传动系统低阶(频率小于10 Hz)振型为一阶扭转振动和上下晃动振动,为了保证传动系统运行时的稳定性,必须保证传动系统前两阶固有频率与风轮工作转频1P、3P、风轮面外一阶挥舞频率、风轮面内一阶摆阵频率避开,偏差不小于10%。
以额定容量1.5 MW的主流风力发电机组为计算对象进行分析,风轮工作转频范围为10.53~17.2 r/min,风轮面外一阶挥舞频率为0.78 Hz,风轮面内一阶摆阵频率为1.48 Hz,坎贝尔图见图9。

图9 坎贝尔图Fig.9 Campbell diagram
从图9中可知,传动系统一阶扭转频率和上下晃动频率与风轮1P、3P、风轮面外一阶挥舞频率、风轮面内一阶摆阵频率在工作转速范围内没有交叉,即没有共振点,但传动系统一阶扭转频率与风轮面内一阶摆阵频率相距较近,偏差为7.5%,小于10%,为了保证传动系统运行的稳定性,考虑通过降低主轴的质量或提高齿轮箱弹性支撑刚度的方式来提高一阶扭转频率。
由于齿轮箱弹性支撑刚度波动较大,控制精度较差,故通过降低主轴质量的方式实现。主轴为空心轴结构,空心孔用于机舱与轮毂之间的电缆铺设,主轴原始设计重量约5 900 kg,空心孔直径为190 mm,现改进设计,将空心圆直径扩大为240 mm,并减小主轴与轮毂连接的法兰盘厚度25 mm,则主轴重量减少约500 kg(占重量的8.5%),利用有限元软件ANSYS对改进后的主轴进行强度分析,在极限工况下最大应力点为313 MPa,远小于材料屈服强度(490 MPa);并进行疲劳计算,累积疲劳损伤小于1,符合设计要求。
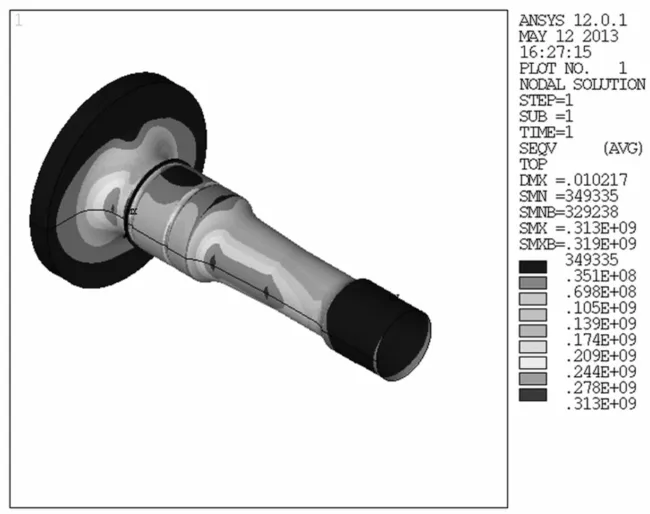
图10 主轴强度分析Fig.10 Strength analysis ofmain shaft
根据动力学方程重新计算传动系统一阶扭转频率,结果为1.68 Hz,与风轮面内一阶摆阵频率偏差为11.9%,超过10%,保证了传动系统运行的稳定性。
另外,风轮转速在升速过程中,当转速为15.6 r/min时,风轮转频3P(0.78 Hz)与风轮面外一阶挥舞频率(0.78 Hz)存在交叉点,利用快速通过控制策略和在发电机端加反向励磁阻尼的方式控制通过时振动能量。
5 结 论
本文通过集中参数质量法建立风力发电机组传动系统四质量块柔性模型,在考虑外部风载、齿轮副时变啮合刚度、啮合阻尼和综合啮合误差激励条件下建立齿轮箱内部各级齿轮副啮合动力学方程。以1.5MW风力发电机组为计算对象,计算传动系统固有频率和齿轮箱各级齿轮动态啮合力,对齿轮箱齿轮啮合力时变特性进行研究,并对传动系统稳定性进行分析,结论如下:
(1)传动系统主要阵型为系统一阶扭转振动、系统上下晃动和齿轮箱行星级耦合阵型、齿轮箱低速平行级耦合阵型和齿轮箱高速平行级耦合阵型,低阶(固有频率小于10 Hz)振型与外部风载激励相关,中高阶振型与内部激励相关。幅值分析,系统主要以一阶扭转振动和上下晃动为主。
(2)齿轮箱内部各级齿轮副在外部激励、时变啮合刚度、和综合啮合误差激励下,齿轮副啮合力呈现高频波动,具有很强的时变特性,通过雨流计数分析,动态啮合力幅值与频次成正态分布规律,为齿轮疲劳受力、轴承承载受力分析提供依据,并为寿命预估建模提供参考。
(3)传动系统一阶扭转振动频率与风轮面内一阶摆阵频率偏差为7.5%,小于规范推荐值10%。通过降低主轴重量约8.5%,提高了传动系统一阶扭转频率约5%,提高后的频率值与风轮面内一阶摆阵频率偏差达11.9%,超过10%,保证了传动系统运行的稳定性,为风力发电机组传动系统设计和可靠性研究提供参考。
[1]Hall JF,Mechklenborg C A,Chen D M,et al.Wind energy conversion with a variable-ratio gearbox design and snalysis [J].Renewalbe Energy,2011,36(3):1075-1080.
[2]Kahraman A,Singh R.Non-linear dynamics of a spur gear pair[J].Journal of Sound and Vibration,1990,142(1):49-75.
[3]Kahraman A,Singh R.Non-linear dynamics of a geared rotorbearing system with multiple clearances[J].Journal of Sound and Vibration,1991,144(3):469-506.
[4]Lin Jian,Parker R G.Analytical characterization of the unique properties of planetary gear free vibration[J].Journal of Vibration and Acousticas,1999,7(121):13-17.
[5]孙涛,沈允文,孙智民,等.行星轮传动非线性动力学建模与方程[J].机械工程学报,2002,38(3):6-10.
SUN Tao,SHEN Yun-wen,SUN Zhi-min,et al.Study on nonlinear dynamic behavior of planetary gear train dynamic model and governing equation[J].Chinese Journal of Mechnical Engineering,2002,38(3):6-10.
[6]孙涛,沈允文,孙智民,等.行星齿轮传动非线性动力学方程求解与动态特性分析[J].机械工程学报,2002,38(3):11-15.
SUN Tao,SHEN Yun-wen,SUN Zhi-min,et al.Study on nonlinear dynamic behavior of planetary gear trainsolution and dynamic behavior analysis[J].Chinese Journal of Mechnical Engineering,2002,38(3):6-10.
[7]朱才朝,黄泽好,唐倩,等.风力发电齿轮箱系统耦合非线性动态特性的研究[J].机械工程学报,2005,41(8):203-207.
ZHU Cai-chao,HUANG Ze-hao,TANG Qian,et al.Analysis of nonliner coupling dynamic characteristics of gearbox systemabout wind-driven generator[J].Chinese Journal of Mechnical Engineering,2005,41(8):203-207.
[8]王旭东,林腾蛟,李润方,等.风力发电机组齿轮系统内部动态激励和响应分析[J].机械设计与研究,2006,22(3):47-49.WANG Xu-dong,LIN Teng-jiao,LI Run-fang,et al.The internal dynamic excitation and response analysis of the gear system for the wind-driven generator[J].Mechnical Design and Research,2006,22(3):47-49.
[9]李润方,陶泽光,林腾蛟,等.齿轮啮合内部动态激励数据模拟[J].机械传动,2001,25(2):1-3.
LI Run-fang,TAO Ze-guang,LIN Teng-jiao,et al.Numerical simulation for inner dynamic excitation of gearing [J].Journal of Mechanical Transmission,2001,25(2):1-3.
[10]李润方,王建军.齿轮系统动力学[M].北京:科学出版社,1996.
[11]王峰,方宗德,李声晋.多载荷工况下人字齿轮传动系统振动特性分析[J].振动与冲击,2013,32(1):49-52.
WANG Feng,FANG Zong-de,LI Sheng-jin.Dynamic characteristics of a double helical gear undermulti-load[J].Journal of Vibration and Shock,2013,32(1):49-52.
[12]何玉林,黄伟,李成武,等.大型风力发电机传动链多柔体动力学建模与仿真分析[J].机械工程学报,2014,50(1):61-69.
HE Yu-lin,HUANG Wei,LI Cheng-wu,et al.Flexible multibody dynamicsmodeling and simulation analysis of largescale wind turbine drivetrain[J].Chinese Journal of Mechnical Engineering,2014,50(1):61-69.
Dynam ic characteristics of a MW class w ind turbine drive system
LUO Yong-shui,ZHOU Min-qiang,CHEN Qi,CUIFeng,LIUWei-jiang
(State Key Laboratory ofWind Power System,Zhejiang Windey Co.,Ltd,Hangzhou 310012,China)
Based on the lumped parametermass standard,a 4-mass wind turbine flexible drive system model was established.Considering externalwind load,gearmesh stiffness,mesh damping and meshing error excitation,its gearbox dynamic equationswere built.A 1.5 MW wind turbine was taken as a calculation object,the natural frequencies of the flexible drive system and the dynamic meshing forces of the gearbox's gear pairs were computed.The statistical analysis wasmad for the gear dynamic meshing forces with the rain flow count method.The results showed that the dynamic meshing forces have strong time-varying characteristics,the proposedmethod provides a guide for gear and bearing design,and their life forecastmodeling.The stability of the flexible drive system was also analysed,the results showed that the deviation between the first order torsional vibration frequency of the drive system and the first order shimmy frequency of the wind turbine rotor is 7.5%,through reducing the weight of the main shaft about 8.5%,the first order torsional vibration frequency of the drive system increases 5%,then the deviation mentioned above is 11.9%,it is 10%larger than the specification value recommended.All results provided a theoretical foundation for wind turbine drive system design and its reliability study.
wind power;flexible drive system;dynamic characteristics;dynamic equation
TK83
A
10.13465/j.cnki.jvs.2015.21.020
2014-08-12 修改稿收到日期:2014-11-06
罗勇水男,硕士生,工程师,1987年7月生

