让“画”深入中职数学课堂
虞倩
【摘 要】在信息高速发展的现代,多媒体辅助数学教学无疑给数学课堂注入了一股“强心剂”。本文就在课堂中利用几何画板创设情境、形成数学概念、启发学生的创新思维等来突破数学教学课堂上的重难点,激发学生学习兴趣;让学生积极参与数学课堂,在做中学,进行讨论。
【关键词】几何画板;中职数学;课堂教学
【现状】:
现状(一):某中职校教室:讲台上老师开始上课“今天我们来学习……”。讲台下学生一片叹息“唉,又要上数学课了。”
现状(二):某中职校教室: “简直天书,我一点都听不懂哦。”“哎,老师这个还是不懂啊!”“烦,烦,烦。”教室里一片抱怨声,学生因为听不懂数学趴着睡觉、讲话、玩手机的现象屡见不鲜。
现状(三):某中职校数学办公室:“唉,现在的学生真难教啊!”“这些学生上课在干嘛都不知道。”“这个题目都讲过的怎么还是不会做哦。”老师们头埋试卷里苦批,一边叹息一边无奈地摇头。
【策略】:
面对这样的现状,作为数学教师的我们应该反思:在传统的数学教学方法中,“一支粉笔写天下,三尺讲台说春秋” 信息的单向传输的教学模式,是不是应该改变了?尤其是学习的主动性以及学习的兴趣上都有待提高的职高的学生。
在课堂教学的形式和内容上都要有所突破,不能一味教师讲解知识和例题。如何设计多样化的数学教学课堂既能关注学生个性差异,又不影响他们的发展呢?笔者认为让学生参与、实践、互动,是有效的方法。用容易学、易操作、功能多的几何画板进行行动导向数学教学,突破难点无疑是个有效的方法。下面结合我的教学实践谈几点运用几何画板进行数学教学整合的体会。
一、运用几何画板,创造数学情境
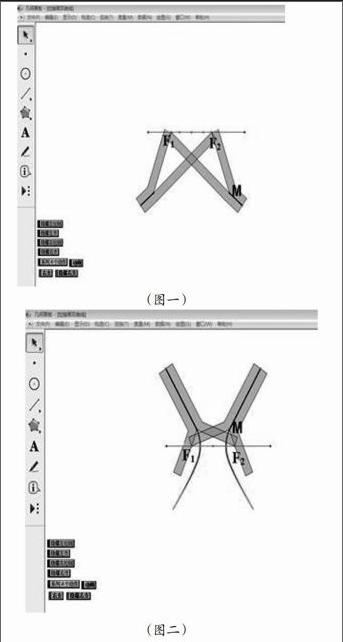
自从有了计算机辅助教学,教师可以更简易丰富生动的为课堂创设一个情境,创设好情境能够促使学生产生学习动力。当然,创设情境的方法也有很多种。而利用几何画板来给学生创设情境给学生的学习提供了直观的数学背景。1.例如在研究“双曲线”的第一课时时,笔者创设了这样的情境:取拉链,拉开一部分,在拉开的A边上取端点固定记作F1,在拉开的B边上在中间部分任取一点固定记作F2(见图一)。注意:F1、F2距离要比拉链上点到F1、F2的距离差要大。把笔尖放在拉链头,随拉链的拉开或者闭合,笔尖就画出一条曲线。接着,固定B变的端点于F1,再任取A边上的中间部分一点固定于F2,同上操作。得到的是什么样的曲线?由于拿实物操作对拉链、笔、按住拉链的位置、时间较难把握因此在课堂上不宜进行实际操作,于是笔者利用几何画板模拟上述过程进行实验得到图二所示,让学生对概念的理解具体形象,而不仅仅只是凭空想象。
(图一)
(图二)
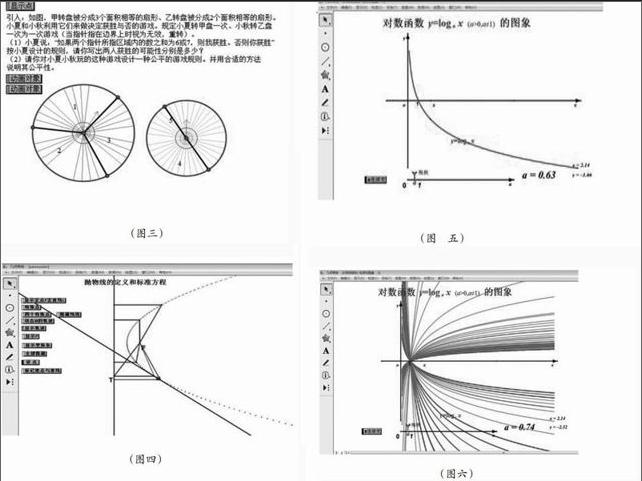
2.如:在学习概率的时候笔者引入了转盘游戏,笔者利用几何画板作了两个转盘提出问题:(如图三)把甲、乙转盘分别分成面积相等的3个扇形及2个面积相等的扇形。小明和小东要来玩转盘比赛。规定小明和小东分别转甲乙盘一次为一次游戏(当指针指在边界上时视为无效,重转)。
(1) 小明说:“如果两个指针所指区域内的数之和为6或
7,则我获胜。如果两指针所指区域内数之和部委6或7则我输”按小明提出意见,请写出小明、小东获胜的可能性是多少?
(2)请对小明小东玩的这个比赛设计公平的规则。并说明原因。让学生亲自动手进行操作实验得到规律。
(图三)
有了这些情景的创设,让学生有更多的机会参与到课堂中来,调动学生的积极性,增加了学生的学习兴趣。
二、运用几何画板,形成数学概念
数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反应形式。利用几何画板使教师能把不容易解释清楚的数学概念解释清楚,是数形结合的一种形式。数学家华罗庚说过:“数缺形时少直觉,形缺数时难入微”。用图形解释抽象的数学概念会更形象、更直观。当抽象的数学概念变为形象的图形时,就能激发学生的学习兴趣,提高学习效率。因此利用几何画板形成概念在解析几何中的使用尤为频繁。例如笔者在讲授抛物线的定义和标准方程的时候也是运用了几何画板进行演示。首先我先显示定点F和定直线L再在平面内选取四个特殊的到点F的距离等于到直线L距离的点,选取其中某个点单击显示菜单的追踪对象(或者按Ctrl+T)开始动画它并追踪点的轨迹。学生恍然大悟原来这个动点的轨迹是抛物线(见图四)。
(图四)
在解析几何中动点形成的轨迹过程是学生最不易理解的,我们可以利用几何画板强大的运算功能和图形图像功能,对动态点进行追踪来显示这个点的轨迹,演示出动点运动的过程,让学生进一步感受到线或轨迹其实是由无数个点组成的。
又如笔者利用课前制作好的几何画板画出y=logax的图像给学生观察下图(见图五):然后拖动点A,改变A在很坐标上的大小也就是改变参数a的大小,这时图像也随之变化起来(适当请学生注意a=1时的图像正好是一条垂直于x轴的直线),接着,还可以选中函数图像,单击显示菜单的
(图 五)
追踪对象(或者按Ctrl+T)再来追踪变化a时图像的变化分布情况。随着多个对数函数图像的显示(如图六),学生就能体会到底数a对函数性态的影响。而当对数函数的图像随着底数的改变而改变时,学生被这个神奇的变化吸引,主动的参与到函数图像的研究中。从图像变化的规律中,学生猜测到函数的性质;接着,笔者引导学生讨论、探索函数的性质顺利的突破本课的难点,突出本课的重点。
(图六)
这两个例子都是利用动态的变化情况来表现静态的数学概念,把抽象的概念具体化,让学生顺利地从感性认识过度到理性认识。克服了以往单调、繁复的教师讲解。使难以理解的概念形象化、具体化,也培养了学生的数形结合的思想。
三、运用几何画板,启发学生的创新思维endprint
创新的敌人是思维定势。爱因斯坦说:“想象力比知识更重要,因为知识是有限的,而想象力概括了世界上的一切,推动着进步,并且是知识进步的源泉。”把几何画板辅助于教学的过程中,几何画板是能够培养学生数学结合思想的,但是否因而阻碍了其他思维能力呢?几何画板作为多媒体辅助教学的工具其实都是为了教学目标和教学重点、难点服务的。因此,只要把几何画板用得适当、适度,也可以培养学生的其他思维能力的。
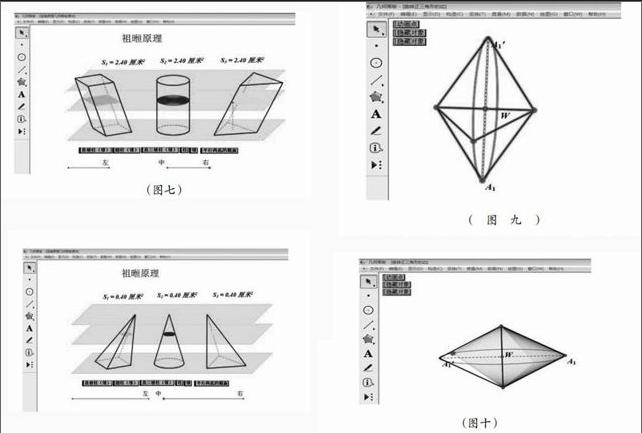
比如在本文的双曲线和抛物线的例子中,动点的轨迹就需要枯燥的代数化以及抽象思维。而几何画板就使得这样的抽象思维具体起来,突破难点 ,达到教学目标。几何画板除了使平面解析几何和函数中抽象概念具体化以外,几何画板还能应用于空间立体几何,培养学生的创新思维。在刚刚接触立体几何时,学生一般都很难想象出空间中的图形,对于学生的空间想象能力的形成就是我们教师急需解决的问题。为了突破这个难点几何画板的动画演示就是我们解决这个问题的利器。1.例如在学习祖暅原理时(见图七)通过课前准备的几何画板课件,动画平行于几何体底面的截面,改变平行于底面
(图七)
的截面的位置(见图八),利用几何画板的测量和计算功能来验
(图八)
证:不管几何体的底面是什么形状,只要几何体之间的高相等、底面面积相等,被平行于底面的平面所截的截面面积相等,则这些几何体的体积就相等。
2.如在某一高职考试的模拟卷中出现了这样的问题(见图九):以边长为4cm的等边三角形,绕其一边旋转一周,则其维持的几何体积为多少cm3?要求几何的体积,就必须知道几何体的形状。对于只接触过以直角边为旋转轴旋转而成的几何体的职高学生无疑这是个难题。单只凭教师的语言表达
( 图 九 )
很难让学生想象出旋转而成的几何体的形状。于是笔者又借助于几何画板强大的动画功能,用追踪线段来演示当以正三角形一边为轴旋转时另外两边所产生的众多画面的变换(见图十),给学生带来视觉感受,这时学生的大脑里就会产生图像空间变化的大致形状,形成了空间想象能力。
综上所述,使用《几何画板》进行数学教学使我们的数学课堂发生了巨大的变化,通过具体的感性的信息呈现,改变了教师的教法,我们的数学课堂不再是“一支粉笔走天下”的教
(图十)
学模式。同时也改善了学生的学法,给学生对课堂中的知识留下更为深刻的印象,使学生通过动手操作、动眼观察、动脑分析对知识留下深刻的印象。从而激发学生的兴趣,提高课堂的学习效率,帮助学生获得更好的学习效果。
【参考文献】
[1]陶维林.《几何画板实用范例教程》[M].北京:清华大学出版社.2001:56-58
[2]张红燕.谈数学课堂的“有效教学”[J].中学数学教与学 2008.1:46
[3]黄新家.概率与游戏问题[J].中学数学月刊2007.2:38
[4]2007年中考自测题——数学[J].今日中学生2007
[5]鞠丹.数学游戏融入初中数学课堂教学的行动研究[J]. 东北师范大学2010endprint