验证“向心力”实验装置的改进

王少鹍

在圆周运动的教学中，难点是对向心力的精确测量。通常情况下教师在教学中只对向心力进行定性研究，教学难点难于有效突破，为此，笔者结合数字化实验，自制了验证“向心力”演示儀，在教学中收到了很好的效果。

向心力数字化实验定量探究在物理教学中，物理概念、物理规律的教学是最核心的内容，而物理实验是物理教学的最重要也是最有效的手段。使用数字化实验来辅助教学，极大地促进了物理新课程改革和教学质量的提高。

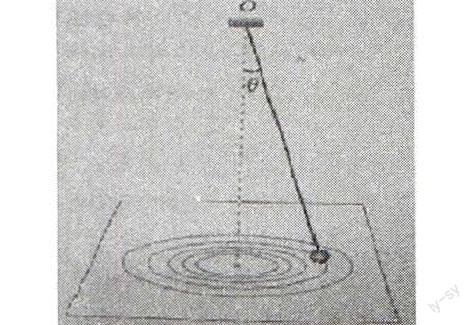
向心力是描述圆周运动的基本物理量，在普通高中课程标准实验教科书物理必修二（人教版）第五章第七节中，演示实验“用圆锥摆粗略验证向心力的表达式”。其实验装置如图1所示：

该装置在验证向心力大小与质量、速度及半径关系时有几点不足：

（1）小球易做椭圆运动，控制小球做圆周运动有难度。

（2）实验操作时，很难做到小球运动的圆周与白纸上的圆周重合，半径的准确测量有困难。

（3）为较准确测量小球圆周运动周期，一般需测量较长时间，小球在运动过程中半径逐渐变小，周期测量误差较大。

（4）可见度小，学生不易观察，实验不具备可重复性。

鉴于以上问题，根据教学实际，笔者结合数字化实验自制了验证“向心力”实验装置的教具，比较有效的解决了上述问题，从而实现了对向心力的准确测量，突破了“准确”验证向心力表达式这一教学难点。现将该实验装置的制作和实验过程介绍如下。

一、实验材料和实验器材

40×70cm钢板一块、固定螺母3个、调平螺丝4个、0.3mm的漆包线、半径2cm，长为60cm的镀锌铁管2根；宽10cm长60cm的横板一块；宽2.5cm，长为60cm的镀锌方管一根。导线若干，开关一个，电源、细绳、橡皮筋、小圆柱体（96.8g）、力传感器、光电门传感器，数据采集器、计算机等。

二、实验装置制作

将两根镀锌铁管与一根方管焊接成“门”字型支架，钢板打孔，用固定螺母把“门”字型支架固定在钢板上；在钢板底部四角安装用以调节水平的底角螺丝，在钢板中央黏合水平仪；将0.3mm的漆包线绕成电磁继电器与电源开关相连并固定于铁管一侧；用细线把小圆柱体与力传感器相连，把传感器固定于“门”字型支架上；两竖杆间架一宽10cm，长60cm的镀锌薄板，两端打孔套于铁管上可沿铁管上下移动，辅以紧固螺丝加以固定；将光电门置于横板上并固定；整个实验装置如图2所示：

三、实验原理

调节力传感器的数据使小圆柱体静止在竖直方向时力传感器的示数为0，这样小圆柱体在摆至最低点时力传感器显示的数值即是摆球在最低点时的向心力。用光电门测出小圆柱体在最低点时经过光电门的时间t。用游标卡尺测出小圆柱体的直径d和高h，用刻度尺测出悬线的长度l。小圆柱体经过最低点时的速度v表示为d/t，小圆柱体圆周运动的半径r表示为l+h/2。小圆柱体的质量m用天平测量。

四、实验过程

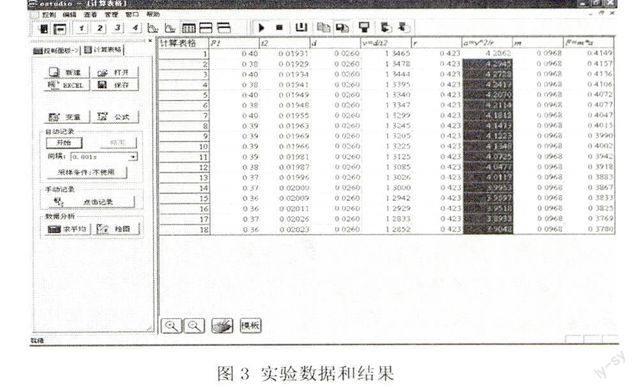
按装置图连接好实验装置；调节力传感器的示数使摆球静止在竖直方向时为0；打开电磁继电器开关，把小圆柱体拉到电磁继电器上被其吸附；断开电磁继电器开关，让小圆柱体在竖直平面内自由摆动；记录小圆柱体摆动稳定后，小圆柱体通过最低点时的力F与时间t的数值；用游标卡尺测出小圆柱体的直径d和高h，用刻度尺测出悬线的长度l；圆柱体经过最低点时的速度v=d/t，小圆柱体圆周运动的半径r=l+h/2；最后用朗威软件来处理数据，如图3所示，得出的结论为：细线的拉力与重力的合力在最低点时与mv2/r相等。

五、教学体会

本实验装置用物体在竖直平面内的圆周运动来代替水平面内的圆锥摆运动，增强了实验的可操作性及可重复性，实验准确验证了向心力的表达式。将物体由电磁继电器吸附，断电使其自由释放，消除了由实验者人工操作时带来的圆周运动的不稳定。本装置采用力传感器、时间传感器可以对F、v进行精确测量，利用数字化实验强大的数据采集能力和灵活的数据处理能力使复杂繁难的实验变得简单易行，有效地突破了教学难点。

传感器、计算机信息技术设备都是物理学发展和进步的成果，将其应用到物理实验教学当中，与时俱进，且能开阔学生的视野，另外学生借助于先进的实验手段，在实验中收获到意想不到的成功，能够激发学生的兴趣和对科学的探索精神。

参考文献：

[1]陈峥嵘.用理想的装备实现教育装备的理想[J].教学仪器与实验，2013，（05）.

[2]冯治山.提高学生物理实验技能浅谈[J].教学仪器与实验，2014，（10）.