加强思维训练 发展思维能力
王花芹
摘要:提高学生的思维能力,是数学教学的首要任务。数学教师在课堂教学中不能只把目光停留在数学知识和解题方法上,而是应该以它们为载体,重点培养学生的思维能力。本文中笔者结合自己的教学实践,谈了两点培养和发展学生思维能力的方法。
关键词:数学教学 思维能力 训练方法
数学是思维的体操,思维是智力的核心。数学离不开思维,离开了思维,数学便失去了意义。所以,数学教学的中心任务就是培养和发展学生的思维能力。下面笔者结合自己的教学实践,着重谈两点培养和发展学生思维能力的训练方法。
一、加强发散思维训练
没有发散思维就没有知识的创新,从某种意义上说,发散思维是创新思维的核心。创新思维要求教师在数学教学中积极地鼓励学生在解题时找出与众不同的解题途径,提出别具一格的解题思路。我认为,在数学教学中培养和发展学生发散思维的方式最重要的莫过于一题多解和一题多变。
1.一题多解。一题多解要求教师在教学中积极地引导学生在剖析数量关系时,用不同的知识进行纵横沟通,以此扩展学生的思维空间,发展学生的思维,这样学生的解题思路就会更加开阔,思维就会更加活跃,十分有利于学生创新。
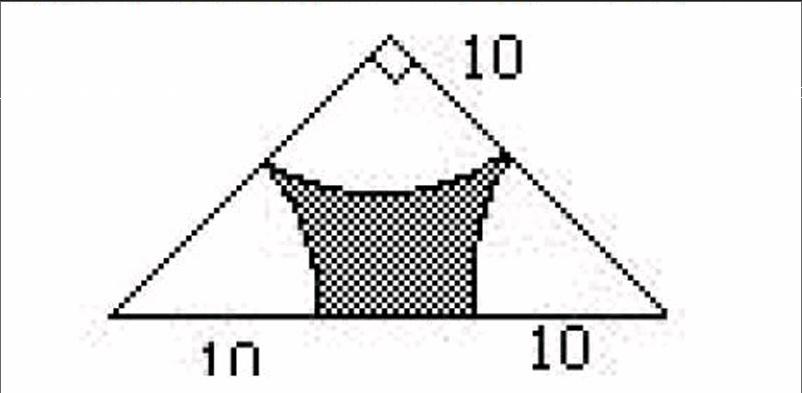
比如,教学六年级的一道几何题:如下图,求阴影部分的面积(单位:厘米)。
分析1:由图我们可以得知此三角形为等腰直角三角形,它的两个锐角都是45°,所以用三角形的面积减去三个扇形的面积之和,就能得到阴影部分的面积。
解法1列式:
分析2:由图我们可以得知三个空白的扇形恰好拼成180°的扇形,所以用三角形的面积减去圆形角是180°的扇形面积,就可以得出阴影部分的面积。
解法2列式:
分析3:同分析2一样,圆形角是180°的扇形面积正好是半圆的面积,用三角形的面积减去半圆的面积,即得阴影部分的面积。
解法3列式:
(10×2)×(10×2)÷2-3.14×10×10÷2
比较以上三种解法,第二种解法优于第一种,第三种解法的思路最灵活,运算也最简便,所以这三种解法中第三种最好。
2.一题多变。一题多变是应用题教学中常用的一种教学手段,它往往在练习课、复习课和思维训练课上使用,可以利用题目中条件和问题的改换,使知识向纵向与横向延伸,使基本题向深度与广度发展,从而让学生对复杂问题的来龙去脉更加清楚。作为教师,我们应该大胆放手,让学生搏击于知识的大海中,创造性地提出问题,进而培养学生开拓和创新的精神。
比如,教学分数应用题,教师可以在黑板上写出两个条件:梨子25个,苹果20个。然后让学生根据这两个条件,提出几个些问题。大家一般会提出以下四个问题:①梨子是苹果的多少倍?②苹果是梨子的几分之几?③梨子比苹果多几分之几?④苹果比梨子少几分之几?
拓展开来,教师将25个梨子用红笔圈起来作为问题,把苹果与上述提出的四个问题的答案作为条件,这样就能形成四个新的问题。如果再把20个苹果圈起来,将上述四题的结果与梨子作为条件,这样就再次形成四个新的问题。
通过一题多变,我们就将梨子与苹果两个基本条件先后组成了十二道基本应用题,这十二道应用题清楚地揭示了分数乘法与除法应用题的转化关系。假如我们再进一步把梨子与苹果的个数和作为标准量时,变化出来的题目就会更多。这些例子只是横向上的一题多变。如果我们在一道基本题的基础上,再附加些条件或者引申问题,那就会形成纵向上的一题多变。这种训练方法,无疑能防止学生思维呆板,使他们摆脱思维定势的羁绊,有利于学生思维灵活性的培养。值得强调的是,运用一题多变有两点需要注意:(1)我们应该把一题多变当作促进学生灵活思维的手段,不能看作是目的,不要为了多变而多变,更不要变得越多越好,一定要根据班级学生的实际情况,安排训练,做到适可而止;(2)我们在训练学生一题多变时,弄清学生是否明确而清晰地掌握了基本数量关系和“量”与“率”的对应关系,因为这一点是一题多变的基础。如果这一点不能掌握,就匆忙起步,仓促地多变,就会适得其反——引起部分学生思维的混乱。
二、加强求异思维的训练
求异思维是指在思维中能够自觉地打破已有的思维定式、思维习惯或以往的思维成果,在事物的各种巨大差异之间建立一“中介”,进而突破经验思维束缚的一种思维方法。它不仅可以通过创造性的思维活动,揭露出事物的本质及内在联系,更主要的是能够在此基础上产生出新颖的、超出一般规律的思维成果。在小学数学教学过程中,培养学生的求异思维,最重要的是开阔学生思路,启发学生从多方面、多角度、多层次思考问题,并在多种结构比较中选择出一种富有创造性的而又超乎寻常的新构思。
比如,在培养学生空间想象能力时,我给学生出示了这样一道题目:“用12根火柴摆出相等的6个正方形,你有这个能力吗?”我先让小组长将准备好的火柴一一发给学生,让他们按照自己的习惯思路在桌面上摆弄,10分钟过后,我对学生的结果进行检查,结果无一人能达到题目要求。这时我引导学生进行联想:“你们学过正方体吗?它有什么特征?”学生齐声回答:“12条棱的长度相等,六个面的面积相等。”这一问,学生的思路打开了,问题解决了,大家异口同声地发出了“噢——”的感叹。
又如,十一册数学课本中有这样一道思考题:“甲、乙两人沿着400米的圆形跑道跑步,他们同时从同一地点出发,同向而行。甲每分钟跑280米,乙每分钟跑240米。经过多少分钟甲追上乙?”对这个问题,学生很难弄明白是什么意思。因为在以往的应用题中都是甲、乙双方,不在同一个起点出发的追击问题,突然出现了在同一起点出发,学生不知如何解答。这时,我就引导学生变换角度思考:甲追上乙,就是甲要比乙多跑一圈,即甲比乙多跑400米。因为改变了思维角度,学生就能轻松地解题了:400÷(280—240)。
如此的求异思维训练,摆脱了常规思维的支配,打破了常规思维的定势,引导学生从新的思维角度思考问题,既在意料之外,又在情理之中。不仅使学生构建了较为完整的知识体系,而且发展了学生多极化的思维方法;不仅防止了片面、孤立、静止看问题的“形而上”,而且使学生所学的知识有所升华。
诚然,培养和发展学生思维能力的训练方法有很多,这里很难一一赘述,但不管运用何种方法,都要因人而异、因时而异、因材而异。只有灵活运用,才能收到预期的效果。