基于加速度传感器的HHT信号降噪方法

杨大为

(沈阳理工大学信息科学与工程学院，辽宁沈阳 110159)

0 引言

传统的信号降噪处理方法是进行信号的频谱分析［1］，如傅里叶分析，得知信号的频率组成成分，采用滤波器滤除干扰频率信号来降低采集信号的噪声，采用这种降噪处理方法就需要预先选定和设计合适滤波器，这就要了解一些先验知识和特定假设。但是在实际情况中，采集到的信号是短时的瞬态信号、非平稳信号、含宽带噪声的，而傅里叶分析对于非线性非平稳信号不适用，此时采用传统的滤波器对信号进行处理，具有一定的局限性。

N.E Huang等学者于1998年提出了希尔伯特黄变换(简称HHT)，是分析非线性、非稳定信号的全新方法［2］。该方法的核心部分是经验模态分解(EMD)，它从根本上克服了Fourier变换的局限性，是一种更具适应性的时频局部化分析方法［3］。通过联合EMD方法与小波阈值降噪滤波，对EMD分解出半数的IMF分量单独进行小波阈值滤波处理，改进了EMD方法在信号降噪处理中丢失有效信号的问题。

1 经验模特分解理论(EMD)

经验模态分解方法认为任意一个信号x(t)都是由一系列不同的、简单的非正弦函数的本征模态函数组成，因而任意一个信号x(t)都可以分解成若干个频率从高到低的本征模态函数［4］。

在实际中采集到的信号都不是IMF，对原始信号x(t)进行EMD分解的具体步骤如下:

(1)首先找出x(t)的所有极大特征值点，采用三次样条插值法拟合出原始数据序列的上包络线eupp(t);同理找出x(t)的所有极小特征值点，拟合出下包络线elow(t)。计算出上下包络线的均值，记为m1(t)

(2)原始数据信号x(t)减去均值m1(t)即可得到一个去除低频的新的数据信号h1(t)，h1(t)=x(t)－m1(t)。如果h1(t)为一个IMF分量则停止分解。

(3)一般h1(t)依然不是IMF分量信号，因而需要对h1(t)重复进行上述处理过程，重复k次直到h1k(t)符合IMF特征的定义要求，所得到的均值趋向零为止。这样就获得了原始信号的第一阶IMF分量c1(t)。

(4)将c1(t)从x(t)中分出来即可得到一个去除高频率分量的信号r1(t)，既有:

为了进一步得到更低频率的分量信号，将r1(t)作为原始信号，重复上述过程得到第二个IMF分量c2(t)。重复n次，直到符合预先设定好的停止规则，最终得到n维IMF分量。

2 HHT理论在信号降噪处理中的应用

由HHT变换过程可知，任意一个信号都可以经过EMD分解成不同频率的IMF分量。可以把一个原始信号经过EMD分解成一定数目的IMF分量，在对各个分量进行相应的频谱分析，然后设计滤波器去除干扰频率IMF分量，再对剩余的IMF分量进行重组［5］。

该重组方式有3种:第一种是低通滤波重组，就是将高频IMF分量去除掉，重组剩余的低频分量组合，复原信号;第二种是高通滤波重组，即将低频的IMF分量滤除，重组剩余的高频分量，复原信号;第三种是带通滤波重组，即保留某个频率段范围内的IMF分量，去除频率范围外的分量，重组剩余的分量复原信号。重复复原信号为:

就是经过HHT降噪处理后的信号。

HHT方法对原始信号进行分解得到不同频率成分的IMF分量，通过对IMF分量进行传统的频谱分析即可得到这些分量的频率成分，通过对采集到的原始信号进行分析，结合一些外界环境影响的因素判断在哪些频率段是完全属于噪声污染，即可去除这个IMF分量［6］。最后将剩余的分量进行重组即可完成对原始信号的快速降噪处理。

由图1对比可看出，含噪声信号经过EMD分解后，得到的IMF分量中前4个IMF分量imf1、imf2、imf3和imf4中包含了大量的噪声频率成分，因此将这4个IMF分量直接去除，重组剩余的IMF分量，即实现HHT低通滤波处理。通过图1的对比可看出，经过HHT降噪处理后的信号明显得到改善，噪声污染明显降低，达到预期的降噪处理效果。

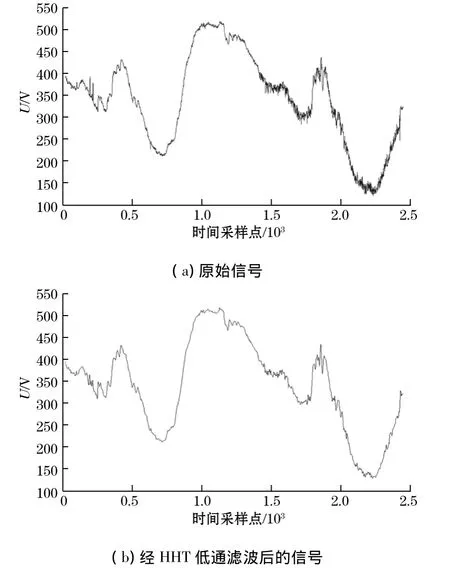
图1 测试信号与HHT降噪信号

3 联合HHT和小波阈值降噪对信号进行降噪处理

对信号进行降噪目的是提高信号的信噪比［7］，为信号的进一步分析提供保障。假如直接采用EMD分解将原始信号分解为一定数目的IMF分量，直接去除含有噪声的IMF分量，对剩余的IMF分量进行重组一定会达到降噪的处理，但是不一定能够提高信号的信噪比［8］。如果对分解出来的各个IMF分量进频谱分析，信号经EMD分解得到N维IMF单分量本征模态函数的频率会依次迅速下降，通过大量信号EMD分解得到第N/2维IMF分量的频率会骤降。由于噪声干扰信号一般表现为相对高频的信号，因此对前N/2维IMF分量单独进行小波阈值滤波降噪处理，之后进行信号重构，最终得到的结果就会得到很大的改善。降噪效果如图2所示。最后联合经过降噪滤波处理的IMF分量和剩余的未处理的IMF分量进行加权和，便可以获得重组出降噪后的信号。

图2 经HHT和小波阀值降噪处理后信号

4 结论

HHT理论中的EMD分解方法从信号自身特点出发，将信号分解成一定数目的IMF分量，通过对IMF分量频率成分的分析，筛选保留包含有效信号的IMF分量，对这些有效成分的IMF分量进行重新组合，达到信号滤波降噪处理的目的。这个过程实际是一个构成高通、低通、带通滤波器的过程，具有十分优越的自适应性。不受信号本身非线性、非平稳性的约束，是一种适用性广泛的提高信号信噪比的方式。

尽管该方法适用性广泛，能够达到降噪的效果，但是由于本身EMD分解过程本身的一些干扰因素，分解出的IMF分量可能同时包含有效频率成分和噪声频率成分。简单的去除包含噪声频率成分的IMF分量，重组剩余的IMF分量已达到降噪的目的是不严谨的，其中存在着丢失有效信号成分的可能，甚至出现严重的信号失真。本文提出对每个分解得到的IMF分量进行频谱分析，对分解出的前N/2个IMF分量单独进行小波阈值降噪处理，最后重组这些经过处理的IMF分量和剩余的未经处理的IMF分量，完成信号的滤波降噪处理。该方法有效的改善了EMD降噪处理过程中丢失有效信号的现象，提高了信号的信噪比。

［1］方新磊，郝伟，陈宏.基于频域滤波的加速度信号处理.仪表技术与传感器，2012(4):94 －96.

［2］吴俊，张榆锋.经验模态分解和小波分解滤波特性的比较研究.云南大学学报(自然科学版)，2012，34(3):285 －290.

［3］李夕兵，张义平，左宇军，等.岩石爆破振动信号的EMD的滤波与消噪.中南大学学报，2006，37(1):150 －154.

［4］王宏禹，邱天爽，陈喆.非平稳随机信号分析与处理.2版.北京:国防工业出版社，2008:96－99.

［5］LI J J，LI X B，QU X L.Signature Analysis Based on Improved EMD with High-order Spline Interpolation.Journal of Networks，2013，8(4):882－887.

［6］ALEXIS Lacout，PIERRE Yves Marcy，MOSTAFA Ei Hajiam，et al.Pulmonary arteriovenous malformations etiologies in HHT patients and potential utility of thalidomide.Medical Hypotheses，2013，80(5):587 －588.

［7］陆兆锋，陈禾，林立，等.压电式加速度传感器在振动测量系统的应用研究.仪表技术与传感器，2007(7):3－9.

［8］路晓妹，寇文珍，段渭军.基于EMD分解重构的互相关时延估计方法.测控技术，2013，32(7):45 －48.