三线摆测转动惯量时高度对测量结果的影响

朱 瑜， 邵雪纯

(湖北民族学院理学院，湖北恩施 445000)

0 引言

转动惯量的测量是高校理工科物理实验教学中一个重要的基本实验［1-16］，其中采用三线摆法测量刚体的转动惯量是常见的一种方法［6-16］，本校使用的实验仪器是由复旦大学物理实验教学中心与上海复旦天欣科技仪器有限公司共同研制并生产的新型转动惯量测定仪。该仪器在测定悬盘的扭转摆动周期时，用激光光电传感器与计数计时仪相结合的方式取代以往用秒表计时的方式，大大减少了计时误差和工作量。实验中，三线摆的高度H对转动惯量的测量结果有较大影响，文献［15］中提出随着R/l比值增大，系统的误差随之增大;文献［16］中指出增大摆长长度，可以减少百分误差。本文通过改变高度(20～110 cm)来分别测量下悬盘、圆盘、圆柱及两叠加圆盘的转动惯量，根据测量误差分析高度对转动惯量测量值的影响。

1 实验数据及处理

1.1 基本参数的测定

悬盘、圆盘以及圆柱质量分别为:悬盘，597.05 g;圆盘 1，227.08 g;圆盘 2，228.11 g;圆柱 1，118.72 g;圆柱2，118.76 g。基本参数的测定结果见表1、2。

表1 上下悬盘几何参数及其间距的测定 cm

表2 圆盘、圆柱体几何参数的测定cm

1.2 转动惯量理论值的计算

下悬盘的转动惯量:

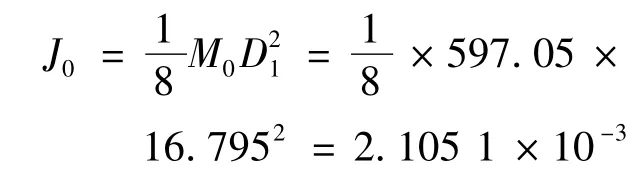
两圆盘的转动惯量:

圆盘2的转动惯量:

圆柱的转动惯量(1个):

1.3 测量结果

本文通过改变高度(20～110 cm，每隔5 cm测1次)，分别测量了下悬盘、圆盘、圆柱及两叠加圆盘的转动惯量，由于篇幅有限，这里仅列出高度为20 cm时的测量数据(见表3)及计算过程，其他测量高度只给出汇总结果(见表4)。

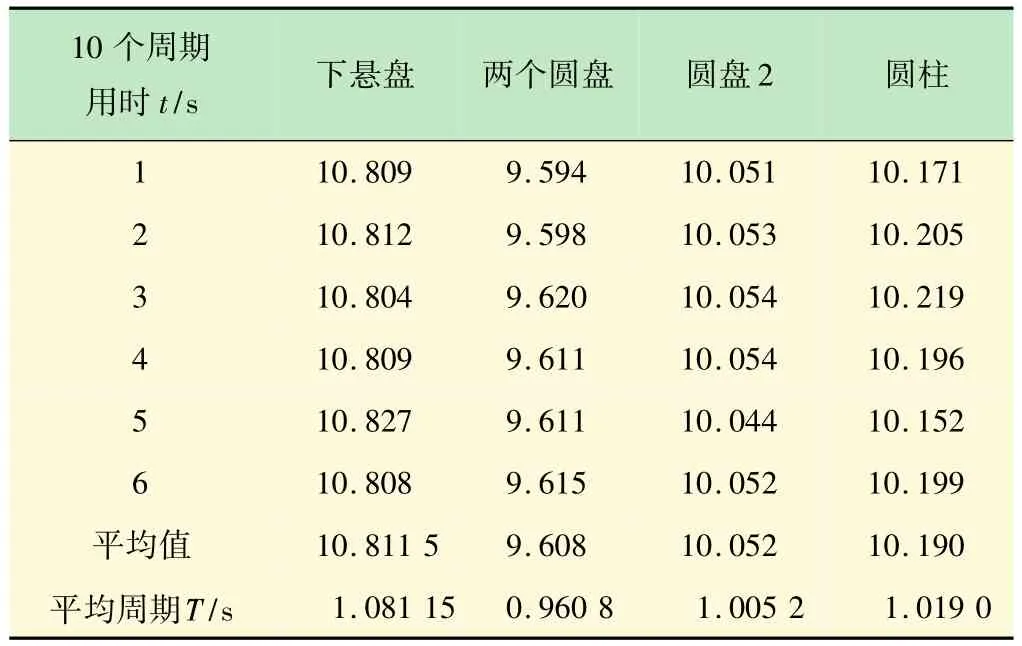
表3 H=20 cm时各待测物的周期测定

例:H=20 cm时各待测物的转动惯量。

①数据计算:

②相对误差计算:

2 结果分析

(1)数据汇总。见表4。

表4 测量各值的百分误差及与理论值比较

(2)数据特点与分析。

①从表4可以看出，当高度在20～110 cm之间变化时，下悬盘、圆盘以及圆柱的测量误差均在3%以内，误差较小，且高度在20～60 cm范围内的测量误差稍小于在65～110 cm范围内的测量误差。这与随着R/l的比值增大，系统的误差随之增大［15］，增大摆长的长度，可以减少百分误差［16］不一致。从测量结果来看，并不是摆线越长，测量结果越好，所以笔者认为，在学生做实验时，高度在20～60 cm更为合适，且取此高度范围，操作方便，仪器的制造上经济实惠。

②比较两叠加圆盘与一个圆盘的测量结果，两叠加圆盘的测量误差明显大于一个圆盘的测量误差，笔者认为厚度的改变影响了测量的结果。当两圆盘叠加在一起时，厚度与一个圆盘时相比明显增加了，其厚度的增加使得测量刚体转动惯量时实际的高度减小了，导致了误差的增加。

③从表4中还可看出，下悬盘的转动惯量的测量值与理论值比较普遍偏大，而圆盘、圆柱的转动惯量的测量值与理论值比较却无此规律。笔者认为下悬盘的测量值比理论值偏大是系统误差所引起的，对圆盘、圆柱而言，在处理数据时，系统误差已被消去，所以圆盘、圆柱的转动惯量测量值与理论值相比时而大、时而小。

3 结论

在用三线摆法测量物体的转动惯量实验中，通过改变高度(20～110 cm)来分别测量下悬盘、圆盘、两叠加圆盘及圆柱的转动惯量，并比较其测量值与理论值的误差。经过分析发现:

(1)当高度在20～110 cm之间时，测得下悬盘、圆盘及圆柱的转动惯量的误差均在3%以内，且高度在20～60 cm范围内的测量误差稍小于在65～110 cm范围内的测量误差。从操作方便、制造经济的角度，高度在20～60 cm范围内更为合适。

(2)两叠加圆盘的转动惯量的测量误差明显大于一个圆盘的测量误差，这说明厚度的增加使得测量的误差增大。

(3)由于系统误差的影响，下悬盘的测量值与理论值相比均偏大，而圆盘和圆柱的测量结果在进行处理时，已消去了系统误差，故与理论值相比时大、时小。

［1］陈莹梅，刘平安.基于垂直轴定理的新型扭摆实验仪的实验研究［J］.实验室研究与探索，2006，25(11):1363-1365.

［2］赵德华.新型转动惯量测量和角动量守恒演示、验证装置［J］.大学物理，2013，32(12):12-14.

［3］朱国全，陈永华.微机配合刚体转动仪测量刚体转动惯量［J］.实验室研究与探索，2005，24(7):26-28.

［4］汪仕元，朱 俊，穆万军，等.对扭摆式刚体转动惯量测量仪载物装置的改进［J］.物理实验，2013，33(5):40-42.

［5］张 娟，周海越，孙迎春，等.双挡光片法测定刚体的转动惯量［J］.物理实验，2013，33(12):30-33.

［6］王玉清，杨能勋，黄保瑞.三线摆加上刚体后振动周期变化的研究［J］.大学物理，2009，28(4):14-17.

［7］赵佳明，刘 峰.“三线摆”实验中摆角限值的讨论［J］.大连大学学报，2000，21(2):54-57.

［8］毛爱华，刘官元，董大明.放置不同物体三线摆转动周期变化规律研究［J］.大学物理，2009，28(4):18-19.

［9］王墨林，罗 乐.“大学物理实验”网络教学系统的设计［J］.实验室研究与探索，2012，31(12):140-144.

［10］李雪梅，夏雪琴.Matlab软件在三线摆法测定圆环转动惯量中的应用［J］.大学物理实验，2014，27(3):101-104.

［11］朱 瑜，潘永丰，左安友.不同摆角对三线摆测量转动惯量的影响［J］.湖北民族学院学报(自然科学版)，2014，32(2):156-158.

［12］赵学荟，侯 文.考虑摆线拉伸效应的三线摆测量转动惯量方法的研究［J］.宇航计测技术，2006，26(6):26-29.

［13］吴 波，朱 瑜，左安友.三线摆转动角度控制装置的设计［J］.大学物理实验，2013，26(2):31-32.

［14］葛宇宏，葛志利.三线摆摆线质量对转动惯量精确测量的影响［J］.力学与实践，2012，34(6):50-54.

［15］葛宇宏.长摆线三线摆大摆角摆动测定刚体转动惯量［J］.机械科学与技术，2010，29(6):792-796.

［16］毕江林，沈一鸣，王 威.三线摆测量刚体转动惯量及其误差分析［J］.科教文汇(上旬刊)，2013，256:86-87.