耦合故障转子系统的降维及动力学特性
曹树谦1, 2, 3,王 俊1, 2, 3,韩研研1, 2, 3,白雪川1, 2, 3
(1. 天津大学机械工程学院,天津 300072;2. 天津市非线性动力学与混沌控制重点实验室,天津 300072;3. 天津大学内燃机燃烧学国家重点实验室,天津 300072)
耦合故障转子系统的降维及动力学特性
曹树谦1, 2, 3,王 俊1, 2, 3,韩研研1, 2, 3,白雪川1, 2, 3
(1. 天津大学机械工程学院,天津 300072;2. 天津市非线性动力学与混沌控制重点实验室,天津 300072;3. 天津大学内燃机燃烧学国家重点实验室,天津 300072)
比较非线性Galerkin法和标准Galerkin法在处理滚动轴承和不对中、碰摩故障引起复杂非线性问题时的降维效果,并用非线性 Galerkin法进一步分析故障转子系统的动力学特性.考虑花键联轴器不对中啮合力,建立不对中-碰摩耦合故障转子-滚动轴承-花键联轴器系统动力学模型,采用两种 Galerkin法对转子系统进行降维,并进行数值仿真,利用分岔图和瀑布图等进行对比分析.结果表明:非线性Galerkin法在处理不对中单一故障及不对中-碰摩耦合故障转子系统所得结果均能与未降维系统较好地吻合,而标准 Galerkin法所得结果则存在一定差别甚至出现降维方法失效;应用非线性 Galerkin法进一步分析故障转子系统发现,尽管降维使故障转子系统的维数减少,但并未改变故障转子的动力学特性,其故障特征信息仍得到保留.
非线性Galerkin法;标准Galerkin法;不对中啮合力;不对中-碰摩耦合故障;转子系统;花键联轴器
随着科学技术的进步,旋转机械正朝着大型化、高速化和大功率、高推力/重量比方向发展,其结构更加紧凑,导致故障发生率也随之增加.基于实际问题所研究的故障转子系统通常为高维复杂非线性系统.对此类强耦合高维非线性故障转子系统直接求解难度较大,并且现有非线性动力学理论虽能够处理低维非线性系统,但很难应用于高维系统.因此,对于大型、复杂高维非线性转子系统的降维方法研究逐渐成为现代非线性动力学研究的热点[1].
对于考虑滚动轴承支撑、不对中、碰摩故障的转子系统,张俊红等[2]基于有限元与数值计算联合仿真方法,建立碰摩-不对中耦合故障柔性转子-滚动轴承系统动力学模型,分析了故障对系统响应的影响.陈果等[3]针对航空发动机整机振动分析,建立了含不平衡-不对中-碰摩耦合故障的转子-滚动轴承-机匣耦合动力学模型,研究耦合故障特征和规律.Zhao等[4-5]考虑不对中啮合力,建立不对中故障转子系统,分析了不对中故障的动力学特性.对于非线性Galerkin法(nonlinear Galerkin method,NGM),基于 Foias等[6]提出的近似惯性流形理论,Marion等[7-8]首次提出了非线性Galerkin法并采用近似惯性流形计算了4维相空间的反应扩散方程.Nelson等[9]考虑到油膜力局部强非线性,将固定模态综合法应用于转子-滑动轴承系统的分析中.Azeezs等[10]应用本征正交分解技术方法分析了悬臂梁和悬臂转子的碰摩运动,结果表明降维后的系统与原系统的动力学特性保持较好的吻合.王晋麟等[11-12]在非线性 Galerkin法的基础上提出了改进的非线性Galerkin法,然后以一个含立方非线性的 5自由度强迫振动系统为例阐明了新方法的有效性,并成功采用该方法对一个双盘转子-轴承系统进行了降维处理.Ding等[13]将标准 Galerkin法(standard Galerkin method,SGM)和非线性 Galerkin法应用于转子-滑动轴承-密封系统,比较了两种方法的降维效果,分析了系统动力学特性.目前,关于综合考虑滚动轴承支撑、不对中、碰摩故障的转子系统动力学模型,对于其中的不对中故障,均未将其考虑为更符合实际的不对中啮合力,未能准确地体现不对中故障的动力学特性.对于考虑不对中啮合力故障的转子系统动力学模型,其未考虑滚动轴承支撑力,而将其简化为线性弹簧,未能准确地反映实际的转子模型,且系统中也未考虑碰摩故障.对于非线性Galerkin法,其在转子系统中的应用还鲜见报道,所建模型大多为滑动轴承支撑且未考虑不对中、碰摩等故障,系统所包含的非线性因素并不复杂.
鉴于此,本文以航空发动机转子系统为研究对象,考虑更加符合实际的不对中故障啮合力,建立不对中-碰摩耦合故障转子-滚动轴承-花键联轴器系统动力学模型.其中滚动轴承力、不对中啮合力、碰摩力都具有很强的非线性且相互影响,形成了复杂的强非线性耦合关系.应用标准 Galerkin法和非线性Galerkin法对该复杂非线性故障转子系统进行降维,采用数值积分法获取降维系统的动力学响应,分析不对中故障及不对中-碰摩耦合故障对系统响应的影响,并比较标准Galerkin法与非线性Galerkin法在处理滚动轴承支撑下两种故障所引起的复杂非线性问题时的降维效果.
1 标准Galerkin法与非线性Galerkin法
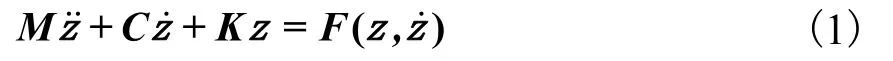
一般的振动方程可写成为系统振动的位移;F为非线性函数;M 和K分别为对称的正定质量矩阵和刚度矩阵;C为阻尼矩阵,采用比例阻尼.则方程(1)的左边可在模态坐标下解耦.
设A=M-1K,令
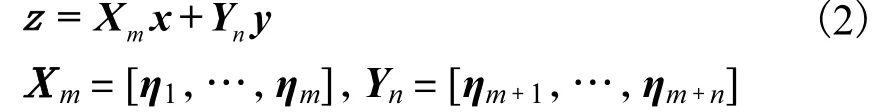
式中:Xm为由矩阵A的前m阶特征向量组成的模态矩阵,对应主子系统;Yn为矩阵A剩余的n个特性向量组成的模态矩阵,对应从属子系统.按照 Xm和 Yn的划分规则,将 AT对应的特征向量划分成和将式(2)代入式(1)并在方程两边同时左乘和,可得微分方程
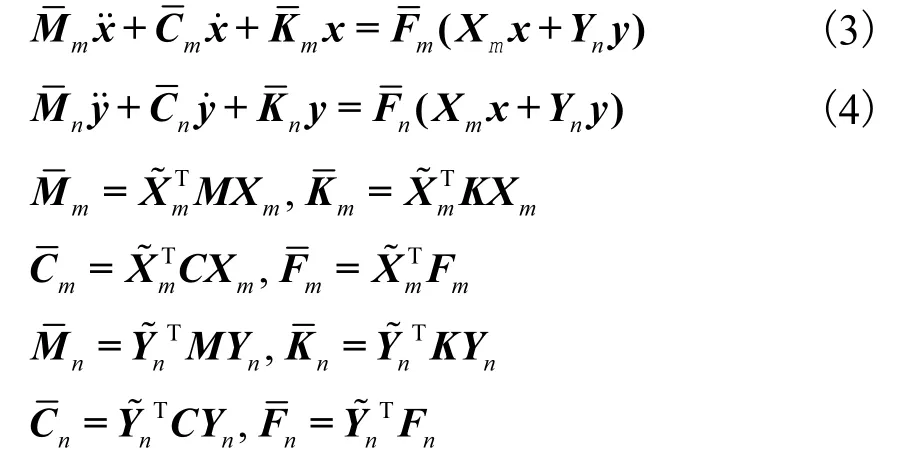
式(3)和式(4)通过非线性项耦合在一起.标准Galerkin法舍弃了高阶模态的影响,即令 y=0,于是得到降维后的方程为
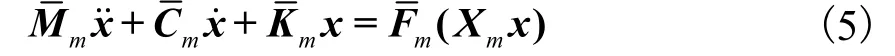
则原系统的近似解可表示为

非线性Galerkin法以近似惯性流形理论为基础,得到 y与 x之间的近似关系[14].令式(4)中的可以得到

式(7)为非线性超越方程,采用 Picard迭代映射求其解.令迭代初值y=0,可得到近似惯性流形为
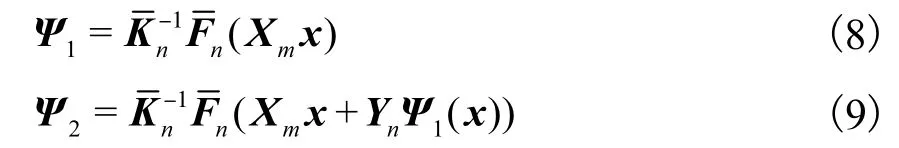
令 y=ψ2(x),将其代入式(3),则可得到降维后的方程为
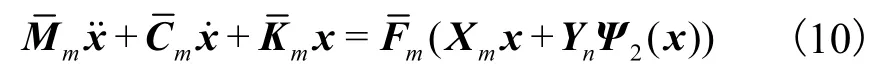
则原系统的近似解可表示为

2 系统模型与基本理论
2.1 转子系统动力学微分方程
图1所示为考虑不对中及碰摩耦合故障的转子-滚动轴承-花键联轴器耦合系统动力学模型,转子采用相同的深沟球轴承支撑.Ms1、Md1、Ms2、Ms3、Ms4、Ms5、Md2、Ms6分别为转子在各节点处的等效集中质量;K为弹性轴刚度;δ为转子与静子的间隙;e1、e2为圆盘偏心距;α1、α2为圆盘偏心角;Ks为碰摩刚度.
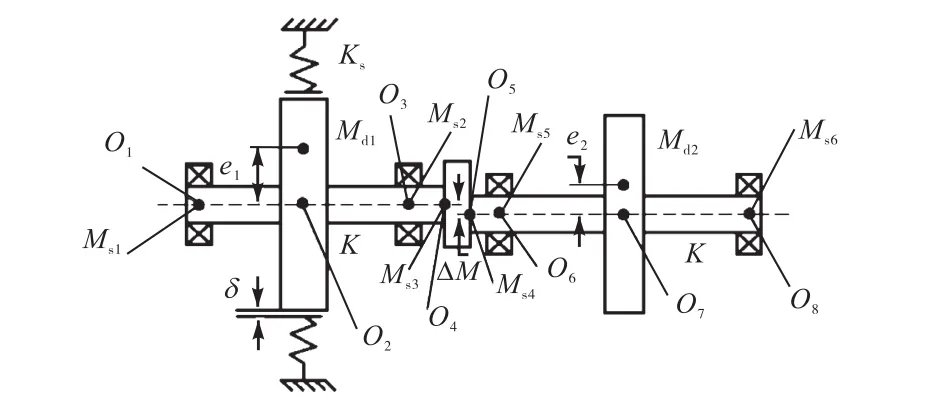
图1 转子-轴承系统简化模型Fig.1 Simplified model of rotor bearing system
根据Lagrange方程,可得系统运动微分方程为
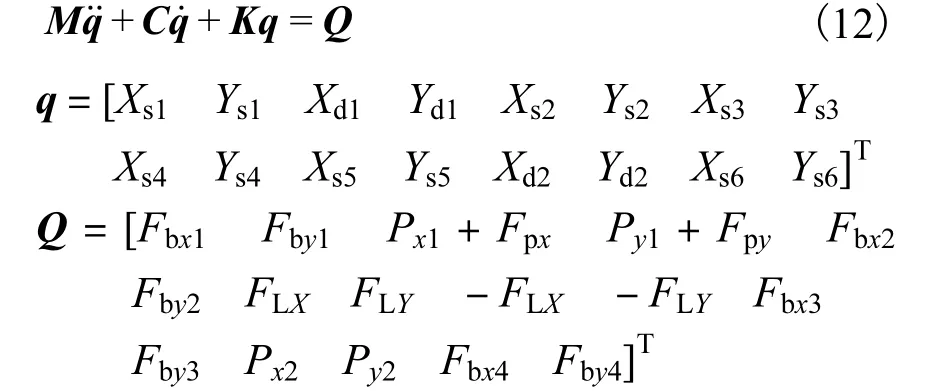
式中:Fbx1、Fby1、Fbx2、Fby2、Fbx3、Fby3、Fbx4、Fby4为各轴承支反力;Px1、Py1、Px2、Py2为各圆盘偏心力;Fpx、Fpy为碰摩力;FLX、FLY为花键联轴器不对中力.
引入无量纲变换
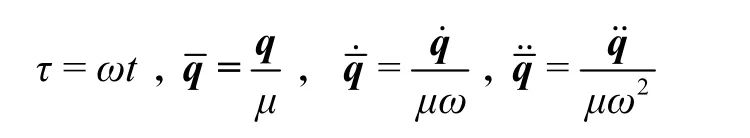
式中:ω为转子转动角速度;μ为滚动轴承游动间隙.式(12)经无量纲变换为
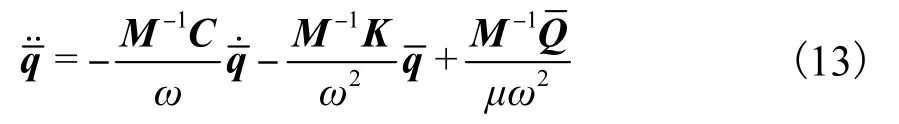
2.2 滚动轴承力模型
图 2所示为滚动轴承受力情况.设轴承滚珠在内外滚道间等距排列,滚珠与滚道之间为纯滚动.由于不平衡激励的作用,滚动轴承做强迫振动,振动频率等于转子旋转频率.同时在旋转过程中,滚动轴承刚度会发生周期性变化,产生VC振动(varying compliance vibration)[15],该振动为参数激振.
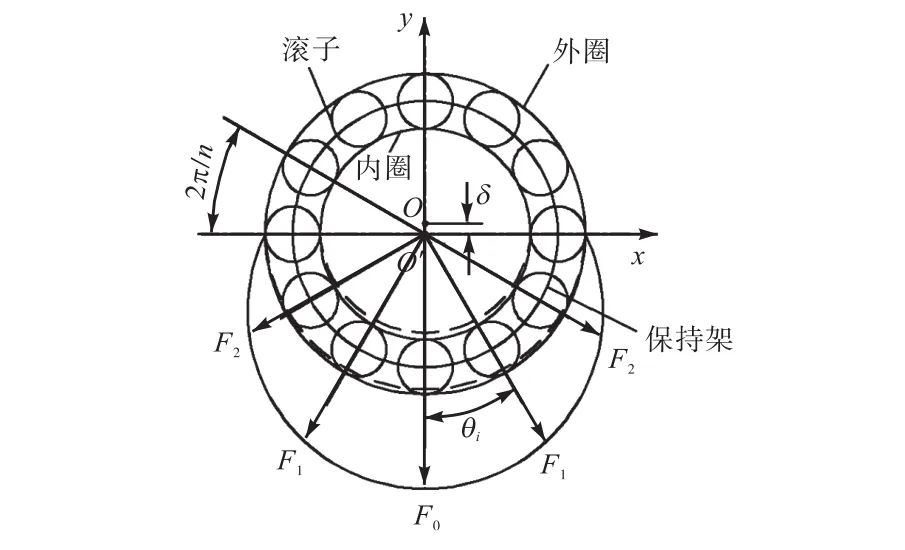
图 2 滚动轴承受力示意Fig.2 Force diagram of ball bearing
基于 Hertz弹性接触理论,参考文献[16-17]可得滚动轴承作用力表达式为
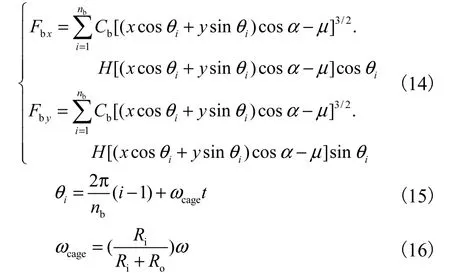
式中:Fbx、Fby分别为滚动轴承力在x、y方向分量;Cb为赫兹接触刚度;nb为滚动轴承滚珠数目;α为滚动轴承接触角;θi为第 i个滚珠角位置;ωcage为滚珠公转的角速度;Ri、Ro分别为内外圈滚道半径;μ为轴承间隙;H(·)为海维赛函数,当括号中的数大于0时,其值为1,否则为0.
2.3 碰摩力模型
图3所示为轮盘碰摩模型,设e为转子圆盘与机匣的径向相对位移,为静止时转子与定子间隙.当 e<e0时,不发生碰摩;当 e≥e0,发生碰摩.假设转子与定子的摩擦符合库仑摩擦定律[18],法向力FN与切向摩擦力FT可表示为
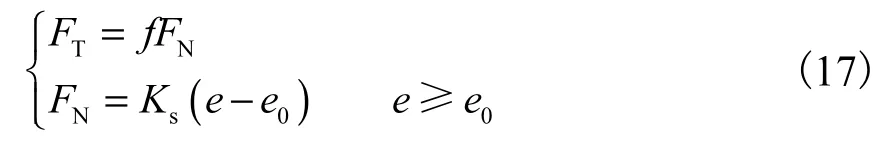
式中f为摩擦系数.将碰摩力沿x和y轴分解可得
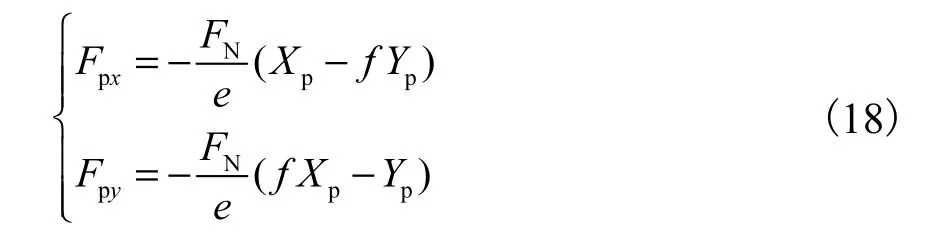
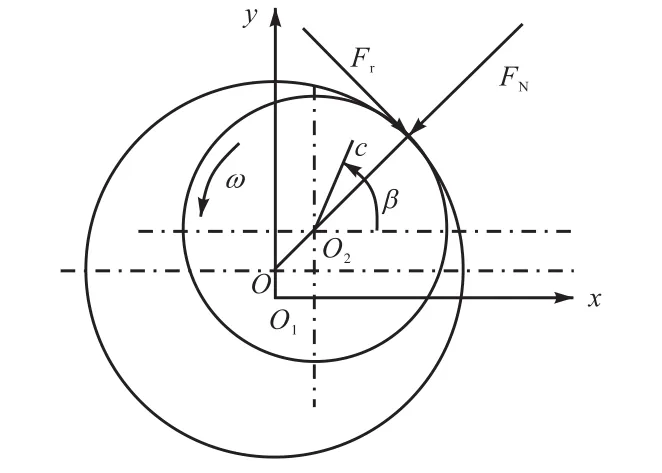
图3 轮盘碰摩示意Fig.3 Rub-impact model of disc
动态位移产生的啮合力为

式中:φi为各键与 x轴正向夹角;e′为联轴器动态径向位移.
综合以上分析,可以得到联轴器不对中产生的啮合力为
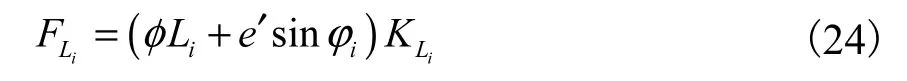
因每一个键的啮合力均不为负,所以
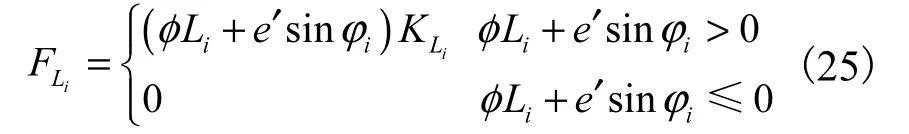
则联轴器不对中产生的x、y向合力为
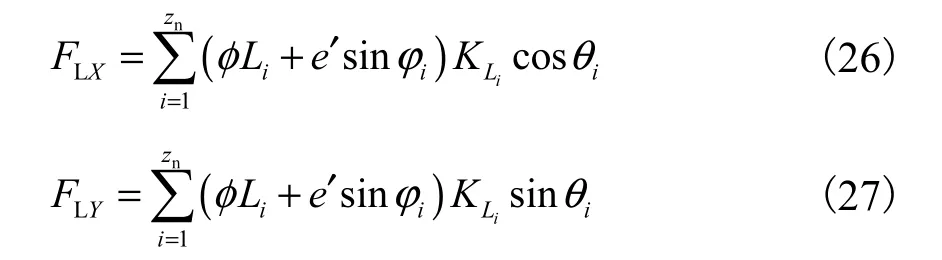
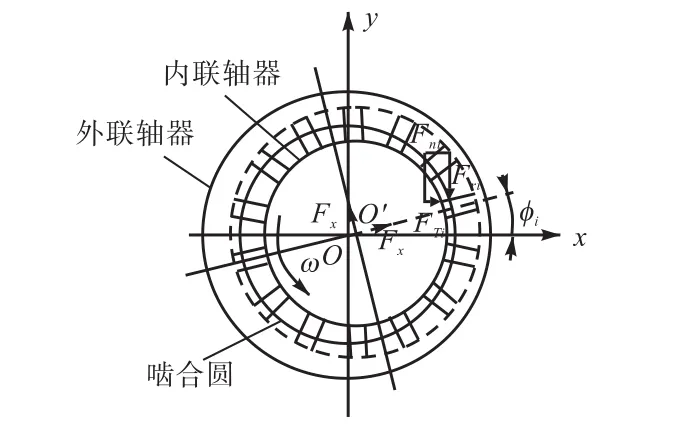
图4 花键联轴器啮合力示意Fig.4 Engaging force diagram of spline coupling
2.4 花键联轴器不对中啮合力模型
图4所示为花键联轴器啮合力示意.联轴器传递扭矩时会使各键发生变形,即扭转使各键产生一个啮合力;同时,两个半联轴器所在节点随系统振动又使各键产生变形,即动态位移使各键产生一个啮合力.
[4-5]可得每个键扭转产生的啮合力为
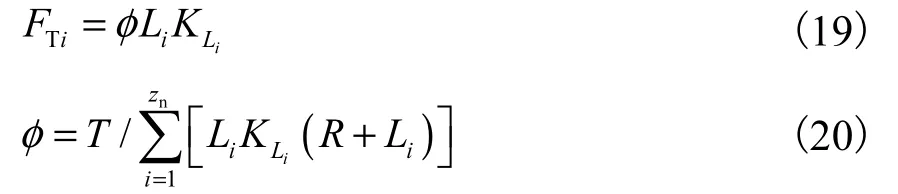
式中:φ 为各键变形产生的扭转角位移;T为扭矩;zn为花键联轴器键的个数;分别为各键等效啮合距离和刚度;R为键根圆半径.
2.5 数值仿真参数的确定
本例选取的转子参数、滚动轴承参数以及花键联轴器参数如表 1~表 3所示,Cz、Cp为转子在轴承、圆盘处阻尼系数.

表1 转子参数Tab.1 Parameters of the rotor

表2 滚动轴承参数Tab.2 Parameters of the ball bearing

表3 花键联轴器参数Tab.3 Parameters of the spline coupling
3 计算结果及分析
3.1 不对中故障下系统的降维计算结果对比及分析
3.1.1 标准Galerkin法和非线性Galerkin法比较
为比较两种 Galerkin法在处理滚动轴承和不对中故障引起的复杂非线性问题时的降维效果,分别采用两种Galerkin法进行数值仿真,并与原系统数值计算结果进行对比.在计算中,标准 Galerkin法截取前10阶模态,对应转子两个弯曲振动方向上前 5阶临界转速;非线性Galerkin法截取前10阶模态作为“主子系统”,剩余的6阶模态作为“从属子系统”.图5~图7分别为原系统、标准Galerkin法降维系统以及非线性Galerkin法降维系统O1节点x方向响应的分岔图以及对应的瀑布图.从图5可以看出,在转速ω∈(500,2,300)rad/s时,系统表现为拟周期运动,如图8(a)所示,在转速为1,600,rad/s时,其Poincaré图表现为一封闭曲线;在转速ω∈(2,300,2,640)rad/s时,频谱图表现为连续曲线,系统进入混沌运动,如图8(b)所示,在转速为2,500,rad/s时,其Poincaré图表现为成片的无规则的密集点;在转速ω∈(2,640,2,690)rad/s时,系统倒分岔进入拟周期运动,如图8(c)所示,在转速为2,660,rad/s时,其Poincaré图表现为一封闭的曲线;转速ω∈(2,690,2,790)rad/s时,频谱图中出现明显的1/2倍频,系统表现为2倍周期运动,如图 8(d)所示,在转速为 2,720,rad/s时,其Poincaré图表现为孤立的两点;当ω>2,790,rad/s时,系统再次进入拟周期运动,如图8(e)所示,在转速为 2,850,rad/s时,其 Poincaré图表现为一封闭的曲线.对比图5~图7可以发现,非线性Galerkin法降维系统和原系统的动力学特性几乎一致,而标准Galerkin法降维系统与原系统动力学特性存在一定的差别.
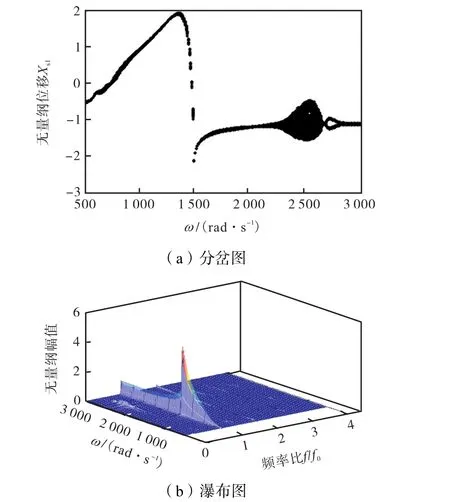
图5 原系统计算结果(不对中故障)Fig.5 Computed results of original system(misalignment faults)
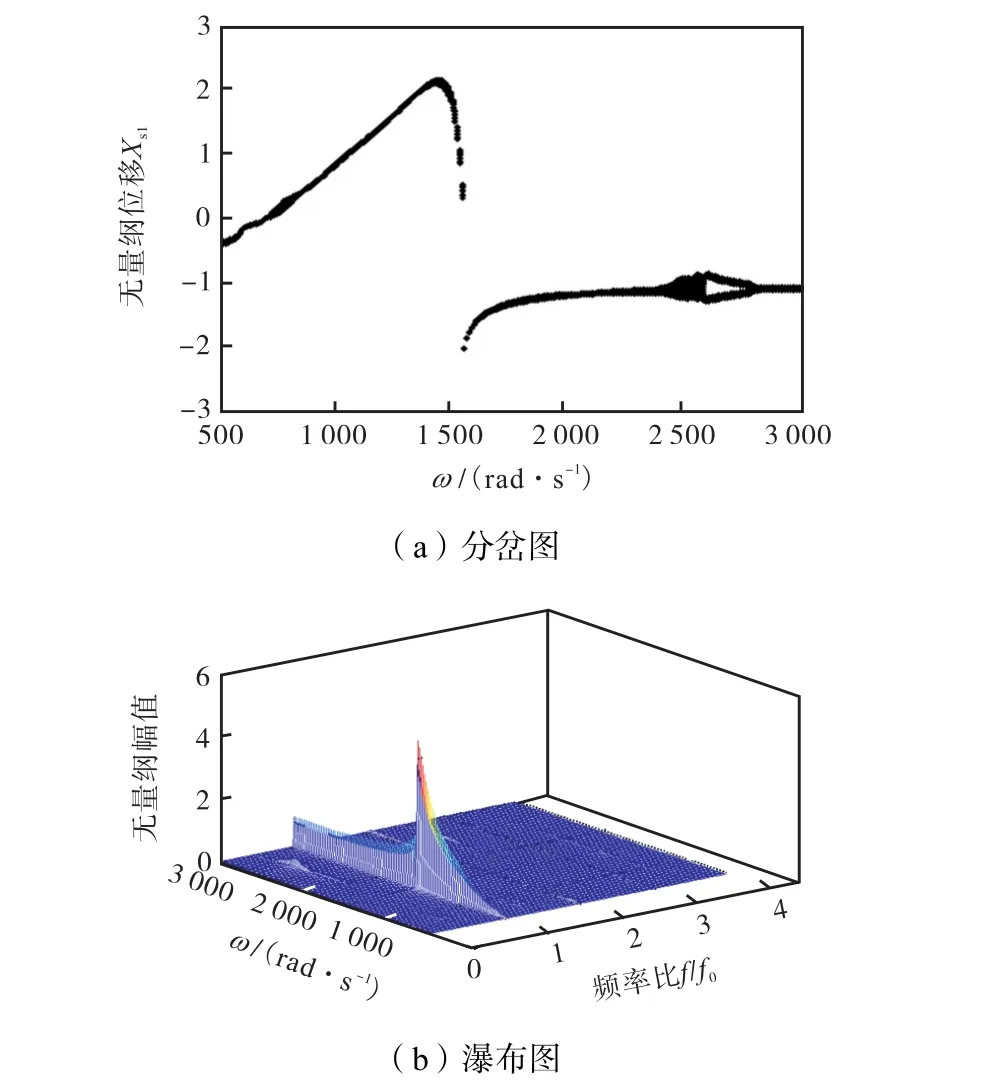
图6 标准Galerkin法计算结果(不对中故障)Fig.6 Computed results of SGM(misalignment faults)
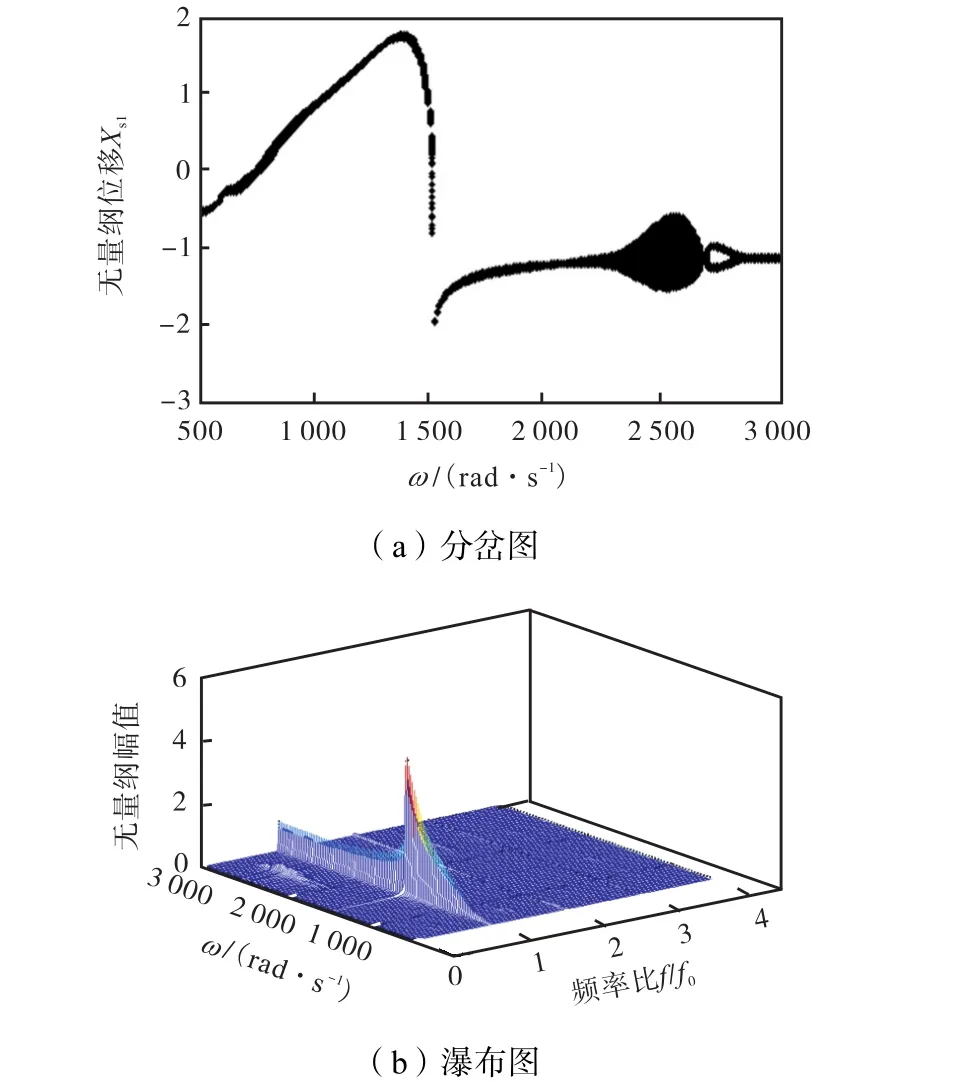
图7 非线性Galerkin法计算结果(不对中故障)Fig.7 Computed results of NGM(misalignment faults)
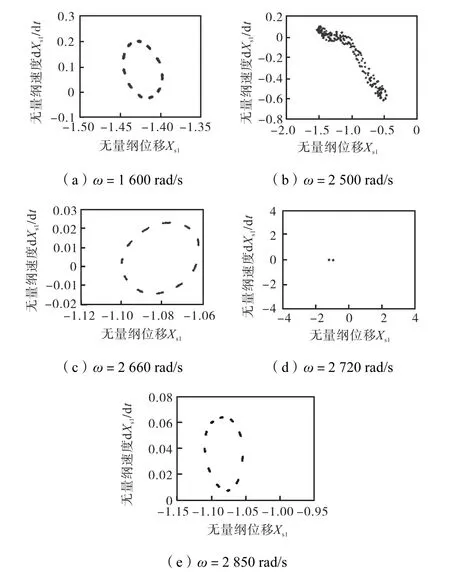
图8 不同转速下系统响应的Poincaré图(不对中故障)Fig.8 Poincaré map of rotor system response at different rotating speeds(misalignment faults)
图 9为随转速变化的幅频曲线.从图中可以发现,随着转速的升高,原系统在转速 1,500,rad/s时幅值出现跳跃,标准Galerkin法出现幅值跳跃时转速为1,560,rad/s,跳跃点发生漂移,而非线性 Galerkin法为 1,520,rad/s,与标准 Galerkin法相比,非线性Galerkin法产生跳跃点的漂移相对较小.此外,随着转速的升高,在幅值出现跳跃前,降维所得的幅值误差逐渐增大,在幅值出现跳跃后,误差逐渐减小,且非线性 Galerkin法所得曲线与原系统几乎重合.与标准Galerkin法相比,非线性Galerkin法所得的随转速变化的幅值与原系统更接近.
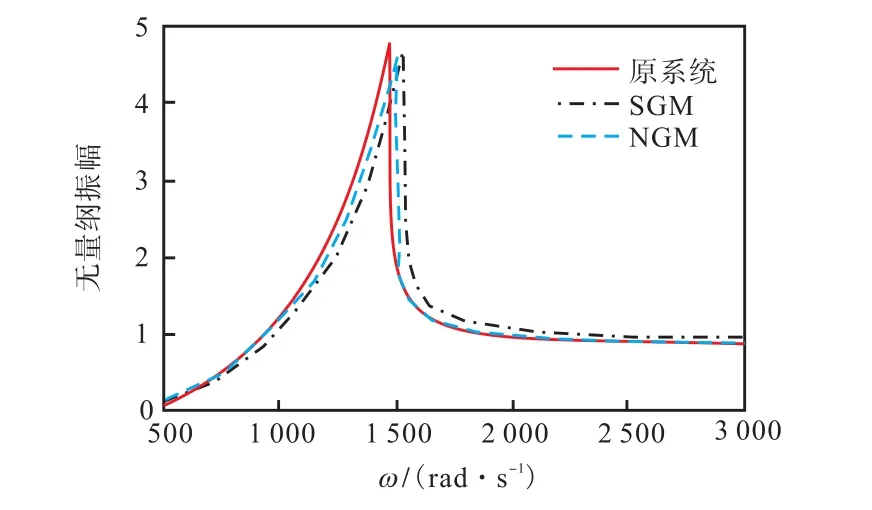
图9 O1节点x向振动幅频特性曲线Fig.9 Amplitude-frequency characteristic curves of O1node in the direction of x axis
图10为不同转速下原系统与两种Galerkin降维方法计算所得的轴心轨迹.在转速为 2,650,rad/s时,非线性Galerkin法所得结果与原系统相似,都为拟周期运动,而标准 Galerkin法所得结果为 2倍周期运动;当转速分别为 2,750,rad/s、2,900,rad/s时,非线性Galerkin所得的轴心轨迹的幅值都比标准 Galerkin法更接近原系统.
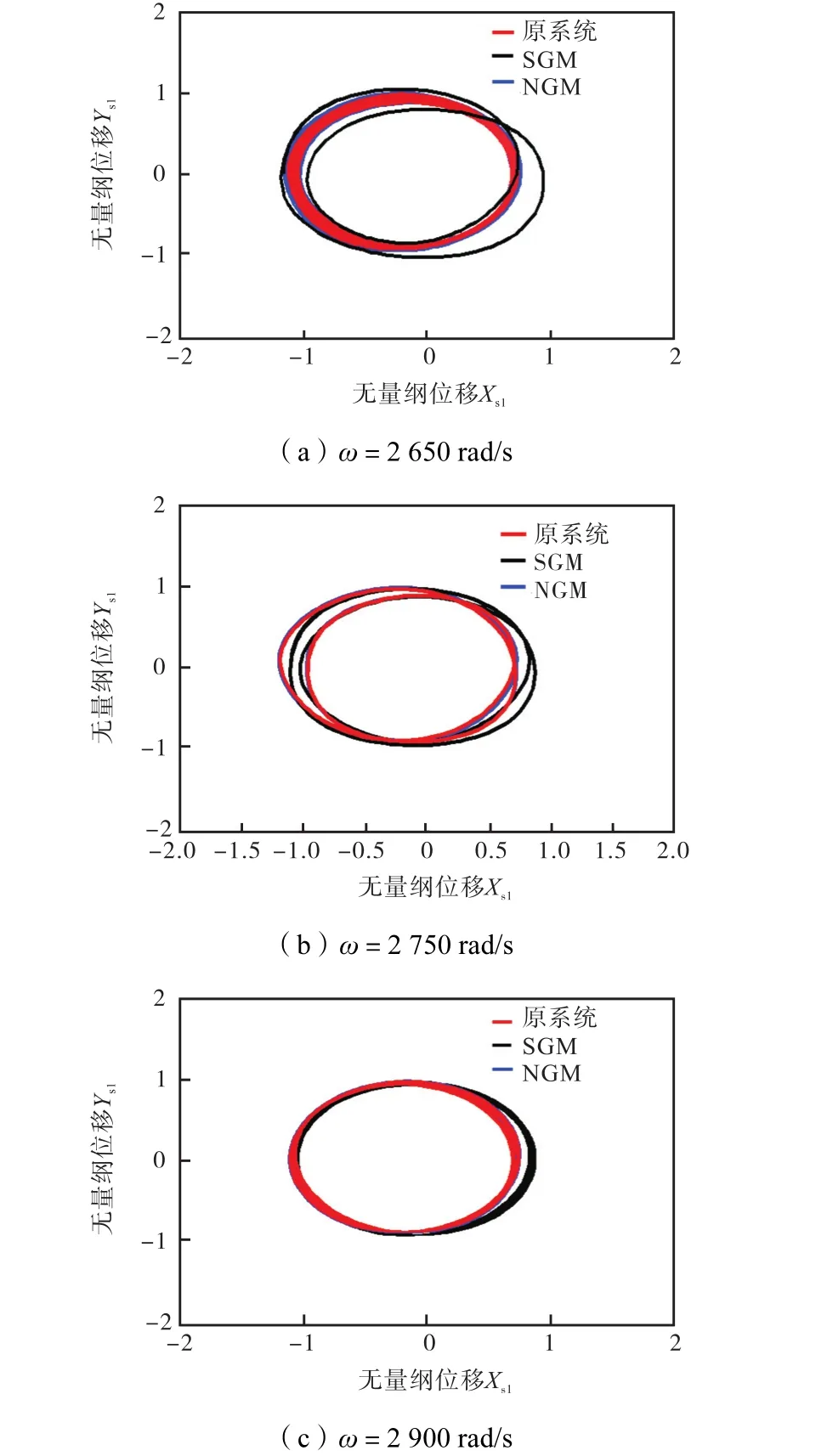
图10 不同转速下O1节点的轴心轨迹(不对中故障)Fig.10 Orbit plot of O1node at different rotating speeds (misalignment faults)
由以上分析可知,在研究滚动轴承支撑下的不对中故障转子系统的非线性动力学响应时,在相同的降维阶数下,由于考虑了高阶模态的影响,非线性Galerkin法比同阶的标准Galerkin法更具有优势,能更好地体现存在滚动轴承和不对中故障的复杂非线性系统的动力学行为.
3.1.2 不对中故障下系统的响应分析
图11为转速ω=1,850,rad/s时不同不对中量状态下 O3节点 y方向响应的频谱.当不对中量为 0时,转子只有 1倍频,存在不对中故障时,出现 2倍频、3倍频及4倍频等高倍频成分,且以1、2倍频分量为主.随着不对中量的增加,3、4倍频等高倍频幅值均有所增大,2倍频幅值呈线性增加,而工频幅值基本保持不变.
图11 ω=1,850,rad/s时不同不对中量下系统响应的频谱Fig.11 Spectrum diagram of rotor system response at different misalignment parameters when ω=1,850,rad/s
3.2 碰摩及不对中耦合故障下系统的降维计算结果对比及分析
3.2.1 标准Galerkin法和非线性Galerkin法的比较
不对中常常会引起碰摩故障的二次效应,产生复杂的非线性耦合关系,表现出更复杂的动力学行为.为比较两种 Galerkin法在处理滚动轴承和不对中及碰摩耦合故障引起的复杂非线性问题时的降维效果,分别采用标准Galerkin法与非线性Galerkin法进行数值仿真,并与原系统进行比较.其中两种方法的降维阶数以及非线性 Galerkin法所考虑的高阶模态阶数均与第 3.1.1节相同.碰摩刚度为 Ks=3× 107,N/m,e0=1.5×10-5,m,其余参数见表1~表3.图12~图14分别为原系统、标准Galerkin法降维系统以及非线性Galerkin法降维系统O1节点x方向位移响应随转速变化的分岔图以及对应的瀑布图.分析图12可知,在转速ω<2,250,rad/s时,系统为拟周期运动,并在转速为 1,550,rad/s附近出现跳跃,如图15(a)所示,在转速为1,600,rad/s时,其Poincaré图表现为一封闭曲线;在区间(2,250,2,780)rad/s,频谱图为连续曲线,系统由拟周期进入混沌状态,如图15(b)所示,在转速为 2,600,rad/s时,其 Poincaré图表现为成片的无规则的密集点;在转速ω∈(2,780,2,890)rad/s时,1/2倍频表现明显,系统由混沌分岔为 2倍周期运动,如图 15(c)所示,在转速为2,870,rad/s时,其 Poincaré图表现为孤立的两点;当ω>2,890,rad/s时,系统再次进入拟周期运动,如图15(d)所示,在转速为 2,920,rad/s时,其 Poincaré图表现为一封闭曲线.对比图 12~14可以发现,非线性 Galerkin法降维系统和原系统的动力学特性几乎一致,而标准 Galerkin法降维系统在转速为1,550,rad/s附近没有出现跳跃且在转速区间(2,300,2,780)rad/s表现为与原系统不同的动力学特性,降维方法失效.
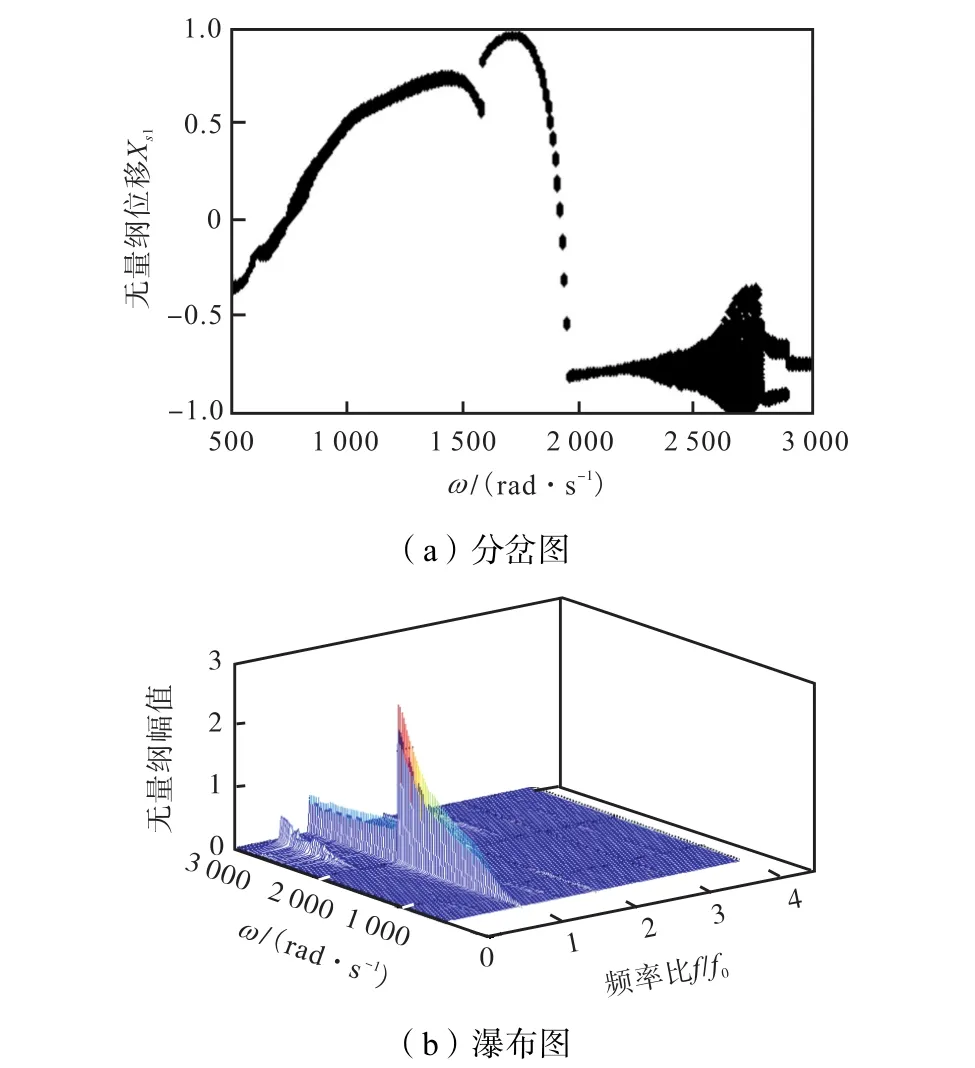
图12 原系统计算结果(不对中碰摩耦合故障)Fig.12 Computed results of original system(misalignment rubbing coupling faults)
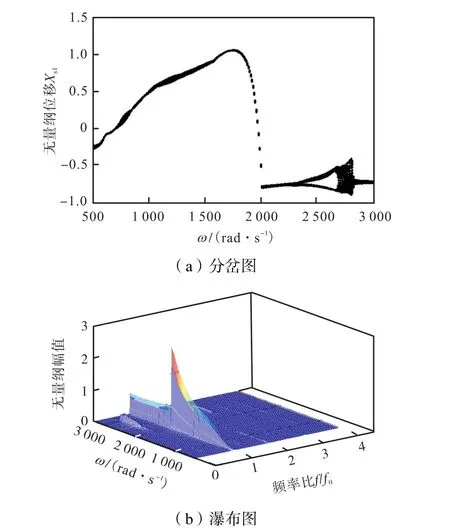
图13 标准Galerkin法计算结果(不对中-碰摩耦合故障)Fig.13 Computed results of SGM(misalignment rubbing coupling faults)
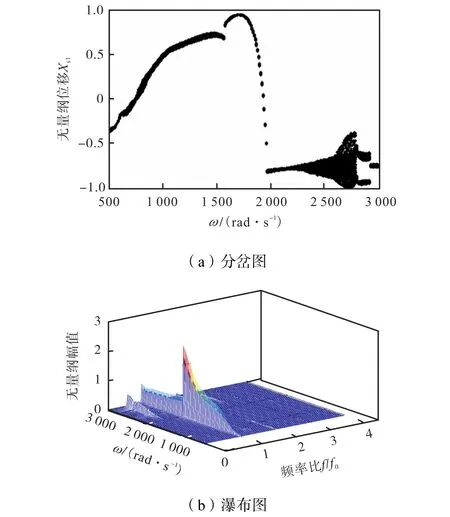
图14 非线性Galerkin法计算结果(不对中-碰摩耦合故障)Fig.14 Computed results of NGM(misalignment rubbing coupling faults)
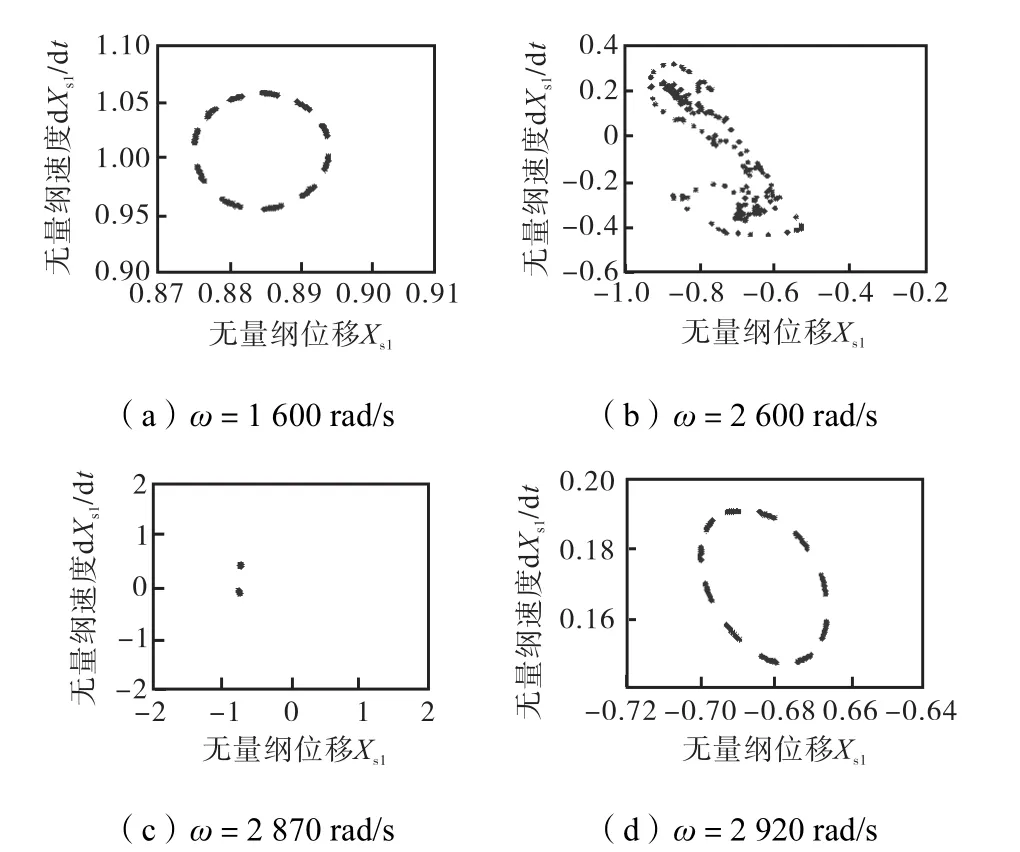
图15 不同转速下系统响应的 Poincaré图(不对中-碰摩耦合故障)Fig.15 Poincaré map of rotor system response at different rotating speeds(misalignment rubbing coupling faults)
图16为不同转速下原系统与两种Galerkin降维方法计算所得的轴心轨迹.在转速为 2,850,rad/s时,非线性Galerkin所得结果与原系统相似,都为2倍周期运动,而标准 Galerkin法所得结果为拟周期运动.当转速分别为 1,960,rad/s、2,950,rad/s时,非线性Galerkin法所得轴心轨迹的幅值都比标准 Galerkin法更接近原系统.
由以上分析可知,在研究滚动轴承支撑下的不对中碰摩耦合故障转子系统的非线性动力学响应时,标准 Galerkin法降维系统与原系统的动力学特性存在较大差别,已不再适用.而在相同的降维阶数下,由于非线性Galerkin法考虑了高阶模态的影响,比同阶的标准Galerkin法更具有优势,能较好地处理复杂非线性问题.
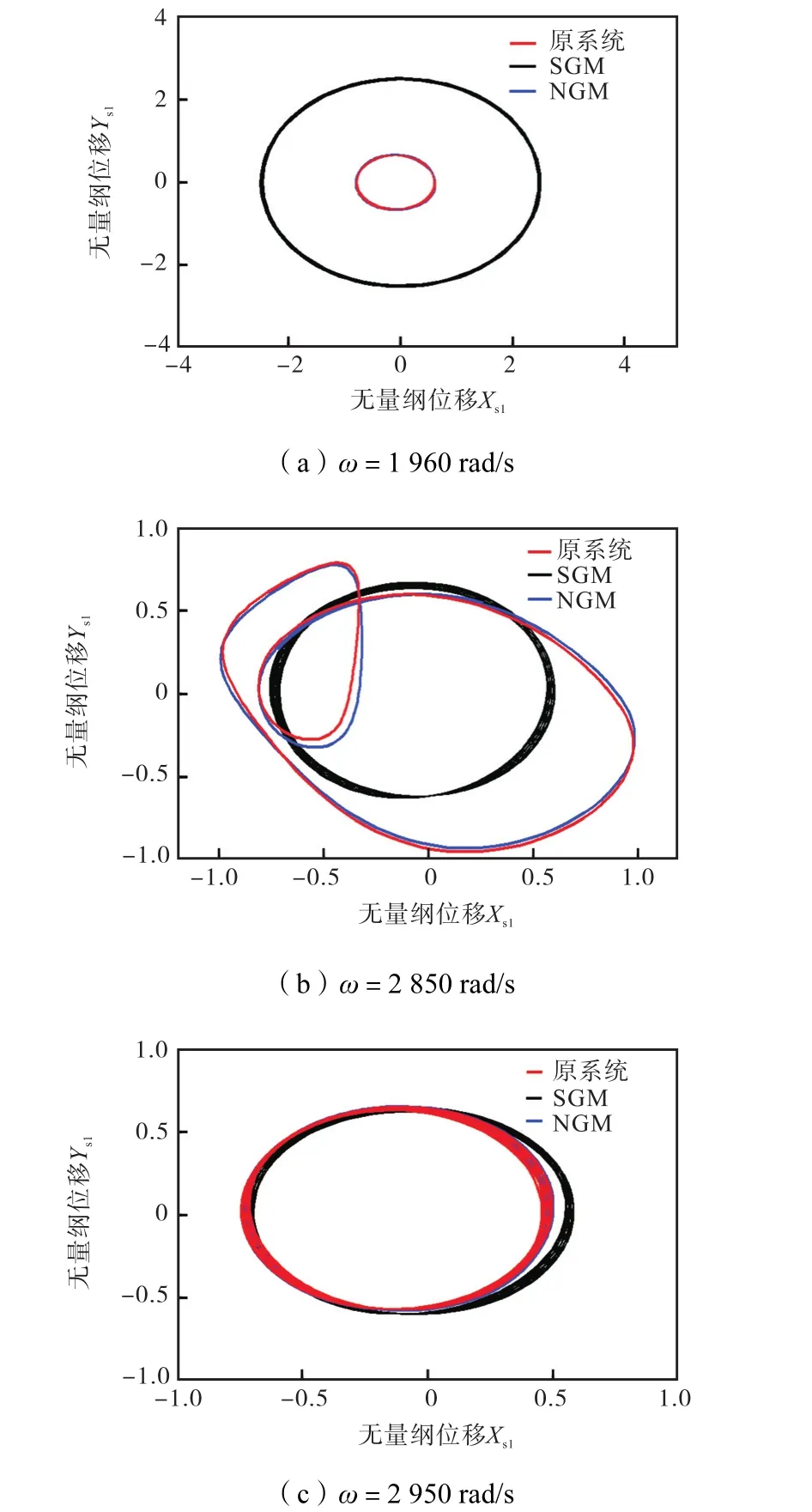
图16 不同转速下 O1节点的轴心轨迹(不对中-碰摩耦合故障)Fig.16 Orbit plot of O1node at different rotating speeds (misalignment rubbing coupling faults)
3.2.2 碰摩及不对中故障下系统的响应分析
对比图 7(a)与图 14(a)可知,由于碰摩的影响,系统的动力学行为变得更复杂,在转速1,550,rad/s附近出现跳跃,此时可能有多个吸引子共存.此外,系统由拟周期进入混沌的转速由 2,300,rad/s提前到了2,250,rad/s,且混沌区间变大.
对比图 7(b)和图 14(b)可知,在转速比较低时,由于碰摩的影响,系统 2倍、3倍等高倍频成分更丰富,分频现象不明显;当转速ω>2,000,rad/s时,碰摩后系统产生大量的分频,而高频现象则不明显.
图17为系统在低转速900,rad/s时O2节点y方向响应时间历程、相图、Poincaré映射以及频谱.从频谱中可以发现,系统存在2倍、3倍等高倍频成分,2倍频成分相对较大,同时存在分频,但表现不明显,系统做拟周期运动.
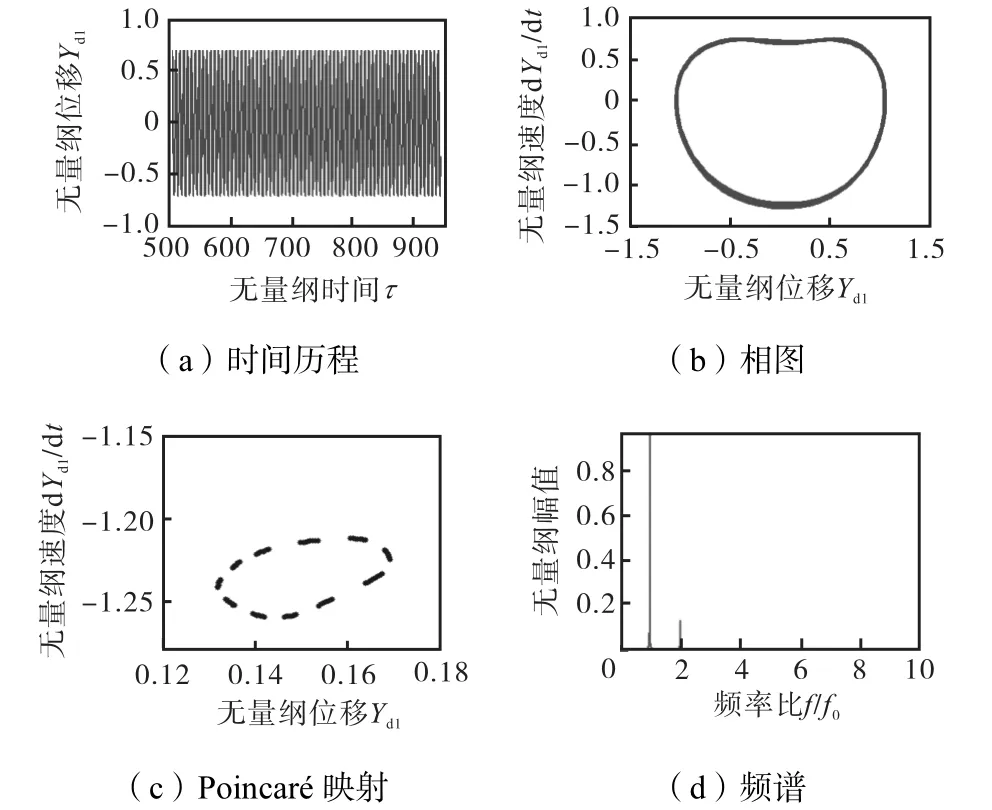
图17 ω=900,rad/s时系统响应的特征Fig.17 Characteristics diagram of system response when ω=900,rad/s
图18为系统在高转速2,800,rad/s时,O2节点y方向响应的时间历程、相图、Poincaré映射以及频谱.从频谱中可以发现,系统存在1/2、3/2等分频,其中1/2倍频表现明显,系统做2倍周期运动.
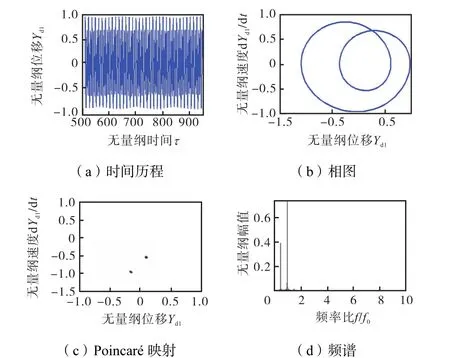
图 18 ω=2,800,rad/s时系统响应的特征Fig.18 Characteristics diagram of system response when ω=2,800,rad/s
4 结 论
(1) 通过对两种 Galerkin法降维系统与原系统的运动分岔图、瀑布图、随转速变化幅值图等进行对比分析可发现,非线性Galerkin法在处理滚动轴承和不对中单一故障引起的复杂非线性问题时所得的结果均能与未降维系统较好地吻合,而标准Galerkin法则存在一定的差别;当综合考虑不对中-碰摩耦合故障时,非线性Galerkin法降维系统仍能较好地与原系统保持一致,而标准Galerkin法降维系统则出现与未降维系统不同的动力学特性,降维方法已不再适用.因此,由于标准 Galerkin法是一种线性降维方法,在处理滚动轴承和不对中、碰摩故障引起的复杂非线性问题时,随着故障因素的增多,非线性耦合关系变得更加复杂,标准Galerkin法逐渐表现出一定的不适应性,甚至出现与未降维系统不同的动力学特性.而非线性 Galerkin法则能较好地应用于复杂非线性故障转子系统的降维.
(2) 应用非线性 Galerkin法进一步分析故障转子系统发现,当存在不对中故障时,系统会产生 2倍、3倍等高倍频成分,且 1、2倍频表现明显.随着不对中量的增加,2倍频成分呈线性增加,而工频基本保持不变.综合考虑不对中-碰摩耦合故障,对比单一故障下的分岔图、瀑布图发现,碰摩使系统产生更复杂的动力学行为,分岔图中出现了跳跃现象,系统的混沌区间变大.在低转速区域,由于碰摩的影响,系统2倍、3倍等高倍频成分更丰富,分频现象不明显;在高转速区域,碰摩使系统产生大量的分频,而高频现象则不明显.因此,尽管降维后故障转子系统的维数减少,但并未改变故障转子的动力学特性,其故障特征信息仍得到保留,从而进一步验证了非线性 Galerkin法能有效地应用于复杂非线性故障转子系统的降维.
参考文献:
[1] 于 海,陈予恕. 高维非线性动力学系统降维方法的若干进展[J]. 力学进展,2009,39(2):154-164.
Yu Hai,Chen Yushu. Recent developments in dimension reduction methods for high dimension dynamical systems[J]. Advances in Mechanics,2009,39(2):154-164(in Chinese).
[2] 张俊红,马 梁,马文朋,等. 不平衡-碰摩-不对中故障耦合作用下柔性转子-滚动轴承系统动力学分析与实验[J]. 天津大学学报,2012,45(10):855-864.
Zhang Junhong,Ma Liang,Ma Wenpeng,et al. Experiment and dynamic analysis of flexible rotor-ballbearing system with unbalance-rubbing-misalignment coupling faults[J]. Journal of Tianjin University,2012,45(10):855-864(in Chinese).
[3] 陈 果,李兴阳. 航空发动机整机振动中的不平衡-不对中-碰摩耦合故障研究[J]. 航空动力学报,2009,24(10):2277-2284.
Chen Guo,Li Xingyang. Study on imbalance-misalignment-rubbing coupling faults in aero-engine vibration[J]. Journal of Aerospace Power,2009,24(10):2277-2284(in Chinese).
[4] Zhao Guang,Liu Zhansheng,Chen Feng. Meshing force of misaligned spline coupling and the influence on rotor system[J]. International Journal of Rotating Machinery,2008,2008(1):321308.
[5] 赵 广,刘占生,叶建槐,等. 转子-不对中花键联轴器系统动力学特性研究[J]. 振动与冲击,2009,28(3):78-82.
Zhao Guang,Liu Zhansheng,Ye Jianhuai,et al. Dynamic behavior of a rotor-misaligned spline coupling system[J]. Journal of Vibration and Shock,2009,28(3):78-82(in Chinese).
[6] Foias C,Manley O P,Temam R. Iterated approximate inertial manifolds for navier-stokes equations in 2-D[J]. Journal of Mathematical Analysis and Applications,1993,178:567-583.
[7] Marion M,Temam R. Nonlinear Galerkin methods[J]. SIAM Journal on Numerical Anaysis,1989,26(5):1139-1157.
[8] Marion M.Approximate inertial manifolds for reactiondiffusion equations in high space dimension[J]. Journal of Dynamics and Differential Equations,1989,1(3):245-267.
[9] Nelson H D,Meacham W L,Fleming D P,et al. Nonlinear analysis of rotor-bearing system using component mode synthesis[J]. Journal of Engineering for Power,1983,105(3):606-614.
[10] Azeezs M F A,Vakakis A F. Proper orthogonal decomposition(POD)of a class of vibroimpact oscillations[J]. Journal of Sound and Vibration,2001,240(5):859-889.
[11] 王晋麟,曹登庆,宋敉淘. 大型动力系统的降维:基于模态截断的非线性Galerkin方法[J]. 动力学与控制学报,2009,7(2):108-112.
Wang Jinlin,Cao Dengqing,Song Mitao. Dimensional reduction of large dynamical systems:An nonlinear Galerkin method based on model truncation[J]. Journal of Dynamics and Control,2009,7(2):108-112(in Chinese).
[12] 王晋麟,曹登庆,黄文虎. 后处理 Galerkin方法在转子-轴承系统降维中的应用[J]. 汽轮机技术,2009,51(5):326-329.
Wang Jinlin,Cao Dengqing,Huang Wenhu. The application of post-processed Galerkin method in rotorbearing systems[J]. Turbine Technology,2009,51(5):326-329(in Chinese).
[13] Ding Qian,Zhang Kunpeng. Order reduction and nonlinear behaviors of a continuous rotor system[J]. Nonlinear Dyn,2012,67(1):251-262.
[14] Steindl A,Troger H. Methods for dimension reduction and their application in nonlinear dynamics[J]. International Journal of Solids and Structures,2001,38 (10/11/12/13):2121-2147.
[15] Harsha S P. Nonlinear dynamic response of a balanced rotor supported by rolling element bearings due to radial internal clearance effect[J]. Mechanism and Machine Theory,2006,41(6):688-706.
[16] Chen G. A new rotor-ball bearing-stator coupling dynamics model for whole aero-engine vibration[J]. Journal of Vibration and Acoustics,2009,131(6):061009.
[17] 成 枚,孟 光. 含 Alford力的非线性转子-滚动轴承系统动力分析[J]. 中国机械工程,2011,22(23):2806-2812.
Cheng Mei,Meng Guang. Dynamic analysis of a rotorball bearing nonlinear system with Alford force[J]. China Mechanical Engineering,2011,22(23):2806-2812(in Chinese).
[18] 李朝峰,李小彭,马 辉,等. 非线性连续转子轴承系统碰摩故障动力学行为研究[J]. 振动工程学报,2009,22(4):395-399.
Li Chaofeng,Li Xiaopeng,Ma Hui,et al. The nonlinear dynamic behavior of a rotor-bearing system with rubimpact by a continuous model[J]. Journal of Vibration Engineering,2009,22(4):395-399(in Chinese).
(责任编辑:金顺爱)
Dimension Reductions and Dynamic Characteristics of Rotor System with Coupling Faults
Cao Shuqian1,2,3,Wang Jun1,2,3,Han Yanyan1,2,3,Bai Xuechuan1,2,3
(1. School of Mechanical Engineering,Tianjin University,Tianjin 300072,China;2. Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control,Tianjin 300072,China;3. State Key Laboratory of Engines,Tianjin University,Tianjin 300072,China)
A comparison was made between the nonlinear Galerkin method(NGM)and the standard Galerkin method(SGM)in terms of dimension reduction’s effect in the solution for complex nonlinear problems caused by the rolling bearing,misalignment faults and friction faults. NGM was further applied to the analysis of the dynamic characteristics of faulty rotor system. Considering the meshing force of misalignment spline coupling,a dynamic model of rotor-ball bearing-spline coupling system with misalignment rubbing coupling faults was established. Both Galerkin methods were used for dimension reduction of the rotor system and a comparative analysis was also conducted,with the aid of numerical simulation,bifurcation diagram,waterfall diagram,etc. Results show that the dimension reduction effect by NGM in dealing with misalignment faulty rotor system and misalignment rubbing coupling faulty rotor system is almost the same as the dimension reduction effect of the system before NGM is applied,while SGM results show some discrepancies and even a total failure of dimension reduction effect. Findings from the analysis of a faulty rotor system in the application of NGM indicate that although dimension reduction can decrease the dimension number of a faulty rotor system,it does not change the dynamic characteristics of the faulty rotor system,with its faulty features unaltered.
nonlinear Galerkin method;standard Galerkin method;misalignment engaging force;misalignment rubbing coupling faults;rotor system;spline coupling
TH133.3
A
0493-2137(2015)04-0318-10
10.11784/tdxbz201310068
2013-10-28;
2014-01-13.
天津市自然科学基金重点资助项目(11JCZDJC25400);天津大学自主创新基金资助项目(2013XZS-0024).
曹树谦(1964— ),男,博士,教授.
曹树谦,sqcao@tju.edu.cn.
时间:2014-02-28.
http://www.cnki.net/kcms/doi/10.11784/tdxbz201310068.html.

