用于电阻层析成像的快速自适应硬阈值迭代算法

董 峰，赵 佳，许燕斌，谭 超

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津市过程检测与控制重点实验室，天津 300072)

用于电阻层析成像的快速自适应硬阈值迭代算法

董 峰1,2，赵 佳1,2，许燕斌1,2，谭 超1,2

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津市过程检测与控制重点实验室，天津 300072)

针对电阻层析成像技术图像重建具有严重病态性的问题，提出了一种稀疏重建算法——快速自适应硬阈值迭代算法，研究了噪声对该算法在电阻层析成像图像重建效果上的影响，并通过仿真和模型实验测试了该算法的性能. 结果表明：一定强度范围内的噪声对硬阈值迭代算法、自适应硬阈值迭代算法和快速自适应硬阈值迭代算法的影响较小. 快速自适应硬阈值迭代算法成像速度更快，且该算法重建图像的空间分辨率相对其他两种算法也有较大的提高.

电阻层析成像；图像重建；迭代算法；硬阈值；自适应

电学层析成像技术出现于20世纪80年代中期，它将传统的局部空间的单点测量方式发展成为对过程参数在二维及三维空间分布状况的在线、实时检测，又由于其具有非侵入、无辐射和成本较低的优点，该技术得到了迅速发展和广泛的应用[1-3]．通过过程层析成像技术获得的有关过程参数的动态信息可以用于优化过程装备、改进流程结构等．

电阻层析成像(electrical resistance tomography，ERT)技术是基于电学敏感性的层析成像技术的一种[4]．由于不同介质具有不同的电导率，敏感场内电导率变化时，电流场的分布会随之变化，最终导致场域边界上电压值的变化．ERT系统通过向被测场域注入电流，同时测量敏感场域边界电压值的变化，进一步对该测量值进行处理，就可获得敏感场内部的相关信息，如流型识别、流速测量及电导分布的图像重建等[5-6]．图像重建作为电学层析成像研究的热点之一，包括正问题和逆问题两部分．由于逆问题求解具有严重的病态性和软场特性，导致它的空间分辨率较低．为了提高图像重建结果，近年来学者们提出了许多的成像算法，它们在成像速度、精度和稳定性上都有了很大的提升．传统的图像重建算法，如共轭梯度算法、Landweber算法、吉普诺夫算法等优化算法都是基于 2范数[7-9]．它们对于光滑信号的效果很好，而对于突变或离散分布的信号，则会增加多余的光滑作用，导致成像效果中有较多伪影．因此基于2范数重建的图像边界容易失真，图像质量不够完美．

随着压缩传感理论的发展，稀疏重建在信号恢复及图像重建领域引起了极大的兴趣[10-12]．硬阈值迭代(iterative hard threshold，IHT)算法，由于计算简单被用于处理许多稀疏信号相关的问题[13-15]．然而，由于缺少有效的自动选择阈值方法，降低了该算法的效率．

为了提高 ERT系统的成像速度和精度，将 IHT算法用于该逆问题的求解，并提出一种快速自适应硬阈值迭代(fast adaptive iterative hard threshold，FAIHT)算法，该算法可以自适应地选择正则化参数，且通过映射方法进一步降低了计算矩阵的维数和噪声对算法的解的影响，使它在成像速度和精度上都有明显提高．

笔者首先介绍了 16电极的 ERT实验系统及灵敏度矩阵的计算，给出了 ERT系统线性化的数学模型；然后给出了图像重建的算法推导；最后，通过仿真与实验验证了算法在成像速度和精度上的优势．

1 ERT系统及其数学模型

1.1 ERT系统

图1为16电极的ERT系统，包括数据采集与控制单元、电极阵列和图像重建单元3部分．电极嵌在内径为125,mm的有机玻璃容器的内壁上．

图1 电阻层析成像系统Fig.1 ERT system

该 ERT系统的工作方式采用电流激励、电压测量模式．当电流通过一对电极施加到被测区域上时，敏感场即被建立．场内电导率的变化将引起电流场分布的变化，进而导致电势分布的变化，使场域边界上的测量电压也发生变化．因此边界测量电压的变

化包含了场域内电导变化的信息，可以通过进一步的处理得到场域内部物场分布的变化．

1.2 ERT数学模型

ERT敏感场的电位分布与电导率分布及激励电流之间的关系满足Laplace方程，即式中：n为边界上一点的外法向量；E为电场强度；σ为电导率；φ为场内电势分布；I为激励电流．

在一定条件下，ERT数学模型能够线性化为

雅可比矩阵通过 Geselowitz的灵敏度理论[16]计算，即

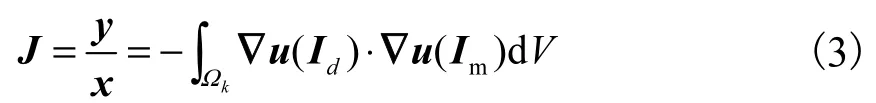
为测量电势.

2 图像重建算法

基于 ERT的图像重建是一个严重的病态逆问题，通过改进重建算法来尽可能逼近其真实解是降低该问题影响的途径之一．

2.1 硬阈值迭代算法

与传统的基于2范数正则化的成像算法相比，稀疏化重建算法能够降低光滑性作用，得到边界更明显的重建图像．基于 l0范数正则化的稀疏重建的目标函数为

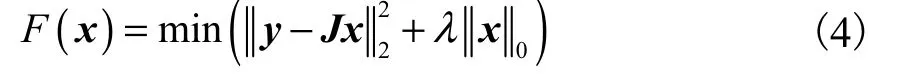
IHT算法，由于其计算量少，收敛速度较快，是一种求解该目标函数非常方便的算法之一．

IHT算法求解过程为

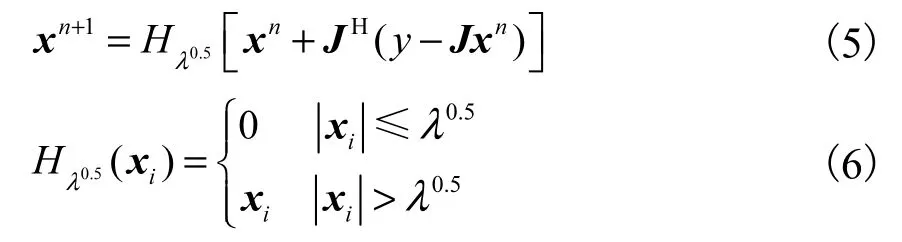
式(6)中参数λ的选择是算法结果好坏的关键问题，它将直接影响到算法收敛速度及求解精度．而参数λ的选择是耗时的，不能够满足 ERT系统实时成像的要求．图2为硬阈值函数，可以发现硬阈值函数计算非常简单，它只是将所有小于阈值的值都置于 0，而不改变大于阈值的值．

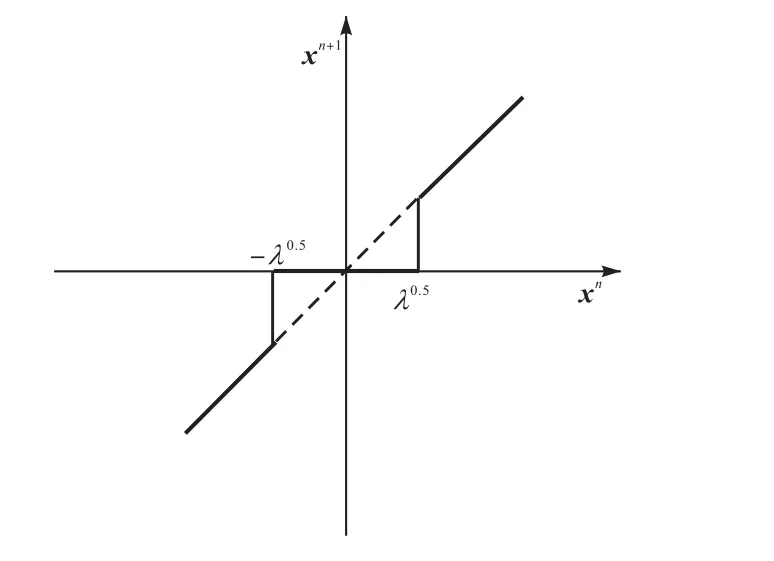
图2 硬阈值函数Fig.2 Function of hard threshold

2.2 自适应硬阈值迭代算法

为了满足 ERT图像重建的实时性要求，同时减少参数选择花费的时间，需要一种能够自动选择参数的方法．文献[17]提出了一种自适应软阈值迭代算法，该算法与映射Landweber算法相比收敛速度跟精度都有提高．该算法的基本思想是通过使软阈值算法每一步迭代得到的结果尽可能地跟 Landweber算法多步迭代的结果相等，这样就可以减少软阈值算法迭代的次数，即提高了算法收敛的速度．这里将该思想用于 IHT算法，提出了自适应硬阈值迭代(adaptive iterative hard threshold，AIHT)算法，希望可以达到同样的收敛效果．算法的具体推导过程为

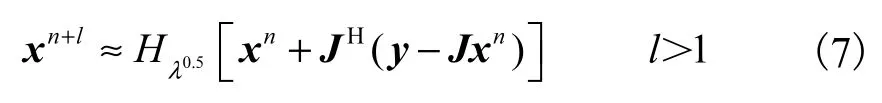
而基于 Landweber算法，可以得到其l步迭代的结果为

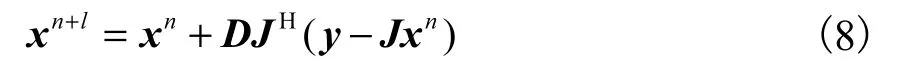
其中

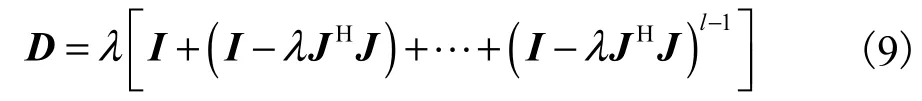
由式(9)可以发现，灵敏度矩阵固定时，D的值只与选定的迭代步数l相关．将式(8)和式(9)代入硬阈值函数，有

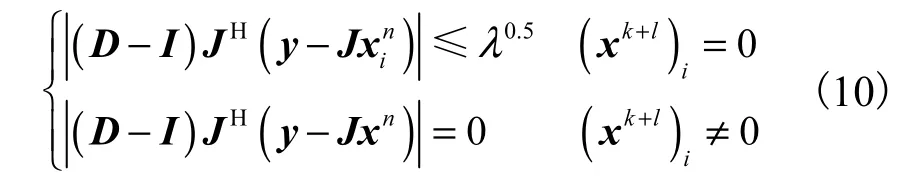
对于整个向量 xn，能够得到

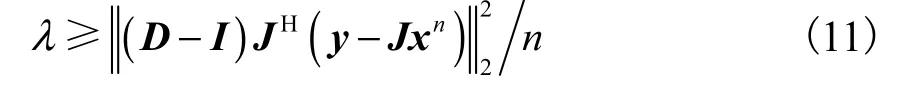
因此，AIHT算法步骤如下：

(1) 选定迭代算法的初始值，如可以通过线性反投影算法给出初始电导估计

(2) 根据式(9)计算矩阵D；

(3) 根据式(11)计算正则化参数λ；

(4) 根据式(5)和式(6)进行计算；

(5) 迭代步数n＋1，从步骤(3)开始重新迭代；

2.3 快速自适应硬阈值迭代算法

IHT算法在初始参数选择上会很耗时，但由于硬阈值函数计算量小，该算法在选定参数后能够较快达到满足要求的解．而AIHT算法由于每步迭代需要重新计算阈值，且灵敏度矩阵的维数较大，因此 AIHT算法的计算速度降低．

为了满足实时成像的目的，本文使用投影方法降低矩阵维数，从而提高算法的收敛速度．这里将灵敏度矩阵和解投影到 Krylov子空间[18]．Krylov子空间定义为

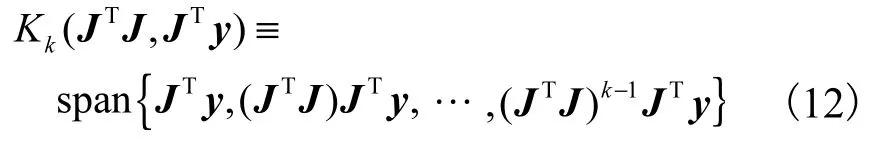
Lanczos双对角化算法用于正交化 Krylov子空间，进而得到 2个正交矩阵和以及1个双对角矩阵．它们之间的关系为

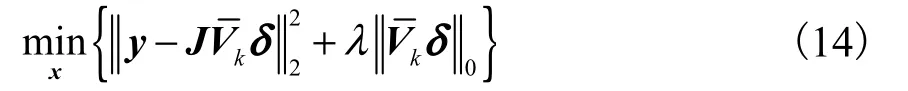
目标函数可进一步简化为

因此，进一步改进的FAIHT算法步骤如下.

步骤1 用Lanczos双对角化算法对Krylov子空间进行分解，并计算矩阵

步骤2 选定迭代算法的初始值，如可以通过线性反投影算法给出初始电导估计(在以下计算步骤中，均用计算得到的代替J).

步骤3 根据式(9)计算矩阵D.

步骤4 根据式(11)计算正则化参数λ.

步骤5 根据式(5)和式(6)进行计算.

步骤6 迭代步数n＋1，从步骤4开始重新迭代.

步骤7 当迭代步数或相邻两次迭代的误差

3 仿真及实验结果

3.1 仿真结果

仿真实验通过MATLAB与COMSOL联合编程实现．有限元方法和毗邻激励模式用于正问题的求解，网格剖分使用 COMSOL默认的三角元剖分．在测试的 3个模型中，异质物体的电导值设为 2,S/m，背景电导值设为 1,S/m．3种算法的最大允许迭代步数为 500，IHT算法的迭代阈值选为 0.000,06．AIHT算法和 FAIHT算法最初的迭代步数l均选为 10，正则化参数λ为 0.000,1，FAIHT算法映射投影维数k选为 40．3种算法都是在迭代步数达到 500或者相邻2次迭代解差的2范数小于0.000,1时终止迭代．

在不考虑噪声作用的情况下，图像重建结果如图3所示．图像重建算法分别为 IHT、AIHT和 FAIHT算法．从图3可以看出，FAIHT算法重建的图像比其他两种方法重建的图像更加逼近真实形状．且FAIHT算法重建图像的伪影相对较少．表 1为 3种算法的重建时间．由于增加自适应选择正则化参数的步骤后，AIHT算法选择正则化参数提高的速度无法抵消其自身优化过程所消耗的时间，因此该算法所耗费的时间反而增加．而 FAIHT算法由于大大降低了矩阵的维数，因此该迭代算法的速度得到显著提高．由表1可以发现FAIHT算法的耗时几乎为IHT算法的1/10．

由于噪声在实际中是不可避免的，对算法的抗噪性也进行了仿真研究．图 4为对每个测量电压施加2%的高斯噪声时 3种算法的重建结果．从图中可以发现，3种算法相对无噪声情况时的重建结果变化不大．这与稀疏化重建算法具有较好的抗噪性相吻合．FAIHT算法重建图像的伪影较其他算法仍然较少，且重建图像更接近真实的电导分布．表 2为图 4中 3种算法的计算时间．可以发现，加入噪声后，3种算法的重建时间没有明显变化，FAIHT算法的重建时间仍然远低于其他两种算法．

为了定量地比较3种成像算法的精度，这里采用相对误差作为判断标准，其定义为

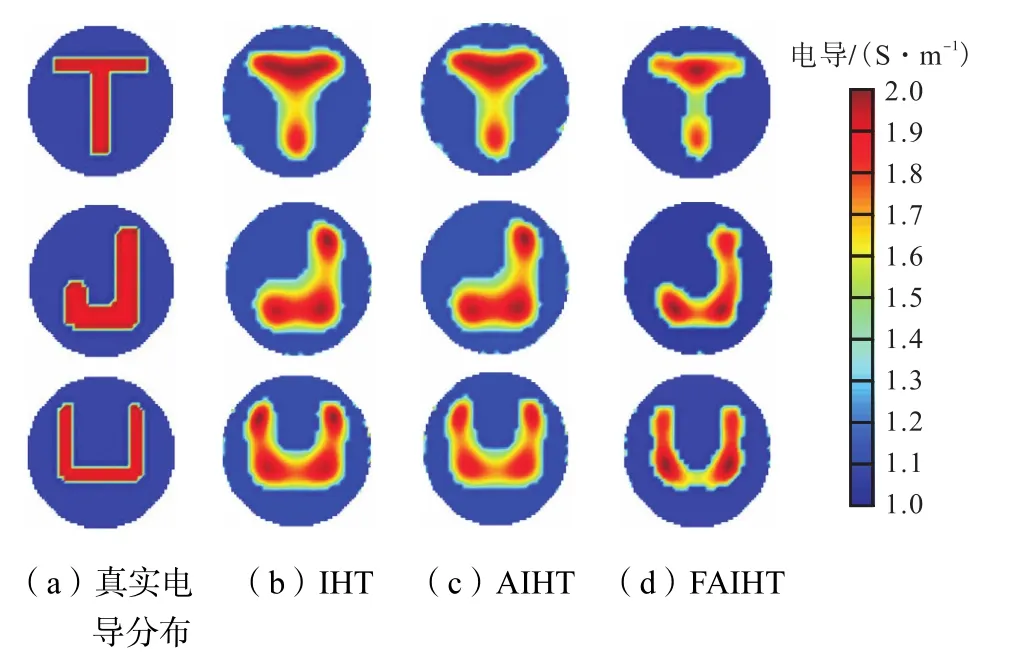
图3 无噪声时3种重建算法的结果Fig.3 Reconstructed images of three algorithms without noise

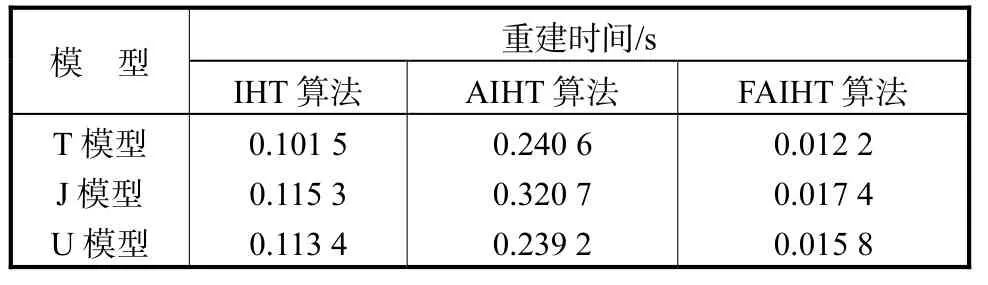
表1 无噪声时3种重建算法的时间Tab.1 Reconstruction time for three algorithms without noise

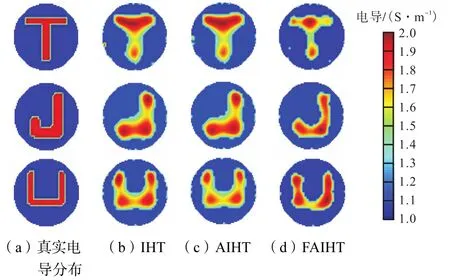
图4 2%噪声下3种重建算法的结果Fig.4 Reconstructed images of three algorithms with 2% noise

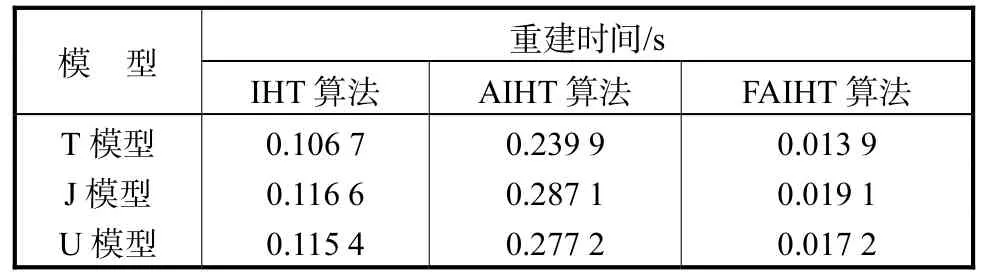
表2 加入2%噪声时3种重建算法的时间Tab.2 Reconstruction time for three algorithms with 2% noise

式中：σ为计算得到的整个成像区域的电导值；σ∗为成像区域的真实电导值．为方便比较，整个成像区域的真实电导率分布值和重建图像的电导率分布值都归一化到1～2,S/m之间．结果如表3和表4所示，表3为3种算法在无噪声情况时对整个成像区域重建图像计算的相对误差，表4为3种算法在2%噪声下对整个成像区域重建的图像相对误差．

可以发现FAIHT算法重建图像的相对误差是最低的，而 AIHT算法重建图像的相对误差要略高于IHT算法．对比表 3和表 4也可以发现，加入 2%的高斯噪声对3种算法重建图像的相对误差影响不大，个别算法的相对误差在加入噪声后反而减小．由以上结果可知，FAIHT算法在有无噪声2种情况下，其求解速度都要明显低于其他2种算法，且计算精度也是3种算法中最优的．

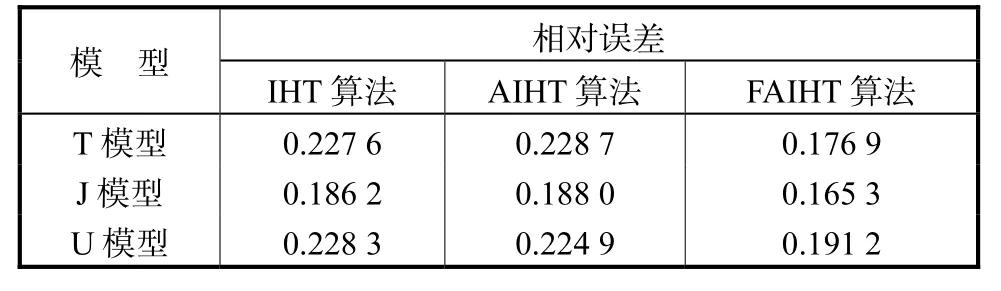
表3 无噪声时3种重建算法的图像相对误差Tab.3 Relative errors of reconstructed images for three algorithms without noise

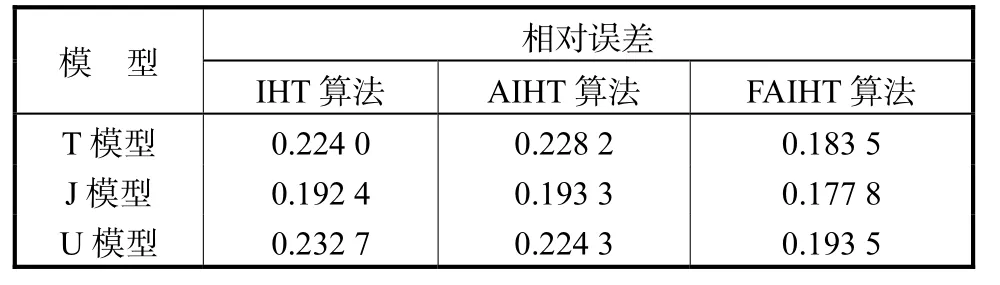
表4 2%噪声下3种重建算法的图像相对误差Tab.4 Relative errors of reconstructed images for three algorithms with 2% noise

3.2 实验结果

图5为模型测试实验中3种算法的图像重建结果．ERT系统采用16电极，毗邻激励测量模式．电极采用高 3,cm、宽 1,cm、厚约为 1,mm的钛合金材料．实验托盘内径为125,mm，4个直径为16,mm的尼龙棒用于成像测试．背景介质采用自来水，电导率约为0.06,S/m，尼龙棒电导率为1×10-12,S/m，激励电流采用幅值为 2.5,mA、频率为 50,kHz的正弦信号．测量电压和重建像素的数据个数分别为 208和812．Krylov子空间的维数为 40．IHT算法的阈值设为 0.000,05，最大迭代步长仍为 500．AIHT算法和FAIHT算法最初的迭代步数l均选为10，正则化参数λ为0.000,03，3种算法都是在迭代步数达到500或者相邻2次迭代解的差的2范数小于0.005时终止迭代．为方便比较，托盘内介质的真实电导率分布和重建图像的电导率分布都归一化到1～2,S/m之间．

尼龙棒的位置分别如图 5(a)所示，IHT、AIHT和 FAIHT 3种算法的重建结果依次如图 5(b)～(d)所示．从图5中可以发现，对于2个尼龙棒和3个尼龙棒的实验，3种算法的重建结果区别不大．对于 4个尼龙棒的实验，IHT和AIHT算法重建的图像与真实分布相差较大，而 FAIHT算法重建的图像与真实尼龙棒分布很逼近，说明 FAIHT算法具有较好的稳定性．表 5为 3种算法重建实验物体分布所花费的时间．与仿真结果类似，可以发现 FAIHT算法的耗时是最少的．表 6为 3种算法对整个成像区域重建图像计算的相对误差．可以发现，AIHT在 2个尼龙棒和3个尼龙棒时重建图像的相对误差较IHT的结果有降低趋势，而对4个尼龙棒重建图像的相对误差远远大于IHT算法．而FAIHT算法重建图像的相对误差一直低于其他 2种算法，进一步表明FAIHT算法具有较好的稳定性和收敛性．

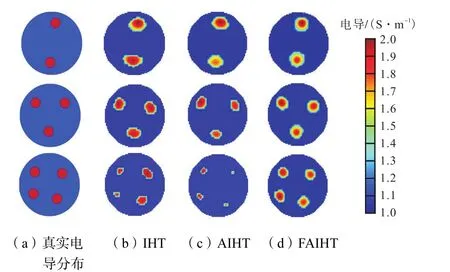
图5 模型测试实验中3种重建算法的图像Fig.5 Reconstrected images of three algorithms in model-test experiments

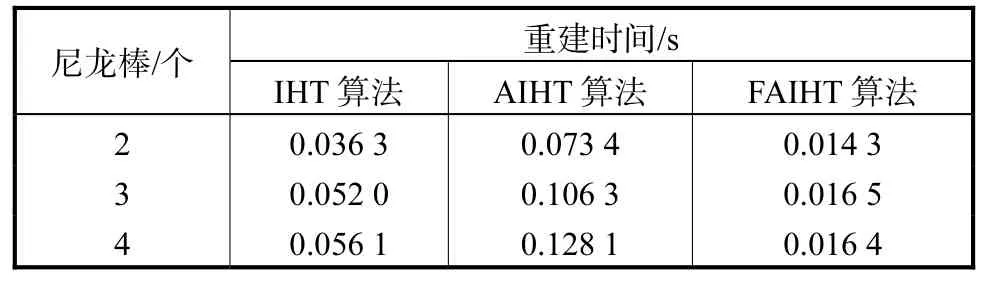
表5 模型测试实验时3种重建算法的时间Tab.5 Reconstruction time for three algorithms in modeltest experiments

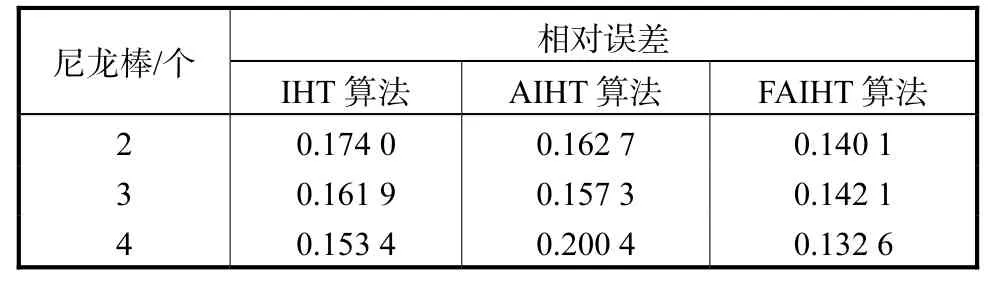
表6 模型测试实验中3种重建算法图像的相对误差Tab.6 Relative errors of reconstructed images for three algorithms in model-test experiments

4 结 语

为了改进 ERT系统成像的速度和精度，提出了一种 FAIHT算法．该算法能够自适应选择正则化参数，重建图像的空间分辨率有了较大提高，且成像速度也有明显提高．由于稀疏化重建算法对噪声的鲁棒性较好，在 2%噪声的情况下，成像误差变化不大，算法具有较好的噪声鲁棒性．仿真与实验结果证明该算法具有较好的噪声鲁棒性和成像精度以及极快的成像速度．

在未来的工作中，更加高效的稀疏化重建方法将用于提高 ERT系统的成像质量及计算时间．此外，其他一些求解正逆问题的方法，如网格分组剖分算法、边界元方法及 L1-L2正则化将用于进一步提高ERT系统的图像重建效果．

［1］ Reinecke N，Mewes D. Recent development and industrial/research applications of capacitance tomography[J]. Measurement Science and Technology，1996，7(3)：223-246.

［2］ 谭 超，董 峰. 过程层析成像与多相流测量应用[J]. 仪器仪表用户，2010，17(1)：3-6.

Tan Chao，Dong Feng. Process tomography and its applications on multiphase flow[J]. Electronic Instrumentation Customer，2010，17(1)：3-6(in Chinese).

［3］ York T. Status of electrical tomography in industrial applicatioins[J]. Journal of Electronic Imaging，2001，10(3)：608-619.

［4］ Dickin F，Wang Mi. Electrical resistance tomography for process applications[J]. Measurement Science and Technology，1996，7(3)：247-260.

［5］ Dong Feng，Jiang Zhixu，Qiao Xutong，et al. Application of electrical resistance tomography to two-phase pipe flow parameters measurement[J]. Flow Measurement and Instrumentation，2003，14(4/5)：183-192.

［6］ 肖理庆，王化祥. 电阻层析成像有限元模型优化[J].天津大学学报：自然科学与工程技术版，2014，47(1)：54-60.

Xiao Liqing，Wang Huaxiang. Optimization of finite element model for electrical resistance tomography[J]. Journal of Tianjin University：Science and Technology，2014，47(1)：54-60(in Chinese).

［7］ Wang Qi，Wang Huaxiang，Cui Ziqiang，et al. Fast reconstruction of electrical resistance tomography (ERT)images based on the projected CG method[J]. Flow Measurement and Instrumentation，2012，27：37-46.

［8］ Trad D O，Ulrych T J，Sacchi M D. Accurate interpolation with high-resolution time-variant Radon transforms[J]. Society of Exploration Geophysicists，2002，67(2)：644-656.

［9］ 李 英，黄志尧，冀海峰，等. 两相流参数测量 ERT图像重建算法的研究[J]. 浙江大学学报：工学版，2003，37(4)：382-385.

Li Ying，Huang Zhiyao，Ji Haifeng，et al. Study on image reconstruction algorithm of electrical resistant tomography for two-phase flow measurement[J]. Journal of Zhejiang University：Engineering Science，2003，37(4)：382-385(in Chinese).

［10］ Tropp J A，Wright S J. Computational methods for sparse solution of linear inverse problems[J]. Proceedings of the IEEE，2010，98(6)：948-958.

［11］ Blumensath T. Accelerated iterative hard thresholding[J]. Signal Processing，2012，92(3)：752-756.

［12］ Bredies K，Lorenz D A. Iterated hard shrinkage for minimization problems with sparsity constraints[J]. SIAM Journal on Scientific Computing，2008，30(2)：657-683.

［13］ Blumensath T，Davies M E. Iterative thresholding for sparse approximations[J]. Journal of Fourier Analysis and Applications，2008，14(5/6)：629-654.

［14］ Blumensath T，Davies M E. Normalized iterative hard thresholding：Guaranteed stability and performance[J]. IEEE Journal of Selected Topics in Signal Processing，2010，4(2)：298-309.

［15］ Foucart S. Hard thresholding pursuit：An algorithm for compressive sensing[J]. SIAM Journal on Numerical Analysis，2011，49(6)：2543-2563.

［16］ Geselowitz D B. An application of electrocardiographic lead theory to impedance plethysmography[J]. IEEE Transactions on Bio-Medical Engineering，1971，BME-18(1)：38-41.

［17］ Dong Xiangyuan，Ye Zhuoyi，Soleimani M. Image reconstruction for electrical capacitance tomography by using soft-thresholding iterative method with adaptive regulation parameter[J]. Measurement Science and Technology，2013，24：085402.

［18］ Jacobsen M. Modular Regularization Algorithms[D]. Denmark：Department of Informatics and Mathematical Modeling，Technical University of Denmark，2004.

［19］ Henk A V. Iterative Krylov Methods for Large Linear Systems[M]. Cambridge：Cambridge University Press，2003.

(责任编辑：孙立华)

A Fast Adaptive Iterative Hard Threshold Algorithm for Electrical Resistance Tomography

Dong Feng1,2，Zhao Jia1,2，Xu Yanbin1,2，Tan Chao1,2
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Process Measurement and Control，Tianjin 300072，China)

In order to reduce the ill-posed problem of electrical resistance tomography，a new sparse reconstruction algorithm named fast adaptive iterative hard threshold algorithm was proposed. The performance of the algorithm was tested in simulation and model experiment. The effects of noise on the reconstructed results of this algorithm were also investigated. Results show that iterative hard threshold algorithm，adaptive iterative hard threshold algorithm and fast adaptive iterative hard threshold algorithm are robust to noise within low intensity range. The fast adaptive iterative hard threshold algorithm has better convergence speed and higher resolution than the other two algorithms.

electrical resistance tomography；image reconstruction；iterative algorithm；hard threshold；adaption

TP29

A

0493-2137(2015)04-0305-06

10.11784/tdxbz201309076

2013-09-18；

2013-10-12.

国家自然科学基金资助项目(61227006，51176141)；天津市自然科学基金资助项目(11JCZDJC22500).

董 峰（1966— ），男，博士，教授，fdong@tju.edu.cn.

谭 超，tanchao@tju.edu.cn.

时间：2013-11-19.

http: //www.cnki.net/kcms/detail/12.1127.N.20131119.1705.001.html.