考虑桥墩－水平梁间弹簧接头的周期性高架桥平面内振动能量带分析

徐斌，徐满清

(南昌工程学院土木与建筑工程学院，南昌 330029)

考虑桥墩－水平梁间弹簧接头的周期性高架桥平面内振动能量带分析

徐斌，徐满清

(南昌工程学院土木与建筑工程学院，南昌 330029)

对无限多跨周期性高架桥结构的周期单元含一个桥墩、二个水平梁及三个连接弹簧，据Bernoulli－Euler梁及Bloch理论，推导具有水平梁－梁、水平梁－桥墩间弹簧接头传递矩阵，建立周期性高架桥结构平面内振动能量带特征方程。据该模型采用数值算例考察桥墩－水平梁刚度比、接头弹簧刚度等对周期性高架桥结构能量带分布特征影响。计算结果表明，具有水平梁－梁、水平梁－桥墩间弹簧接头的周期性高架桥结构发生平面内振动时，高架桥结构中存在与轴向压缩、横向剪切及弯曲振动对应的三类晶格波，即衰减较快且沿高架桥结构传播距离较短、只在某些频域能传播、除较小频率时难以传播外其它较宽频域均能传播。分析结果表明，高架桥结构设计时须保证结构基本主频不能落在较小频率区域，否则极易引起振动波能量集中，造成结构破坏。随周期性高架桥结构水平梁刚度、水平梁－梁接头弹簧刚度增大，沿高架桥结构传播的晶格波衰减会减慢，振动波能量沿高架桥结构会传播更远。

周期性高架桥;传递矩阵;Bloch理论;晶格波;弹簧接头

高速铁路、公路等工程中为有效解决软土地基沉降问题广泛采用高架桥结构。为设计、施工便利，一般高架桥结构采用等跨形式，因此可将多跨高架桥结构作为周期结构，其周期单元包括桥墩及水平桥梁。设计中为保证结构正常安全使用，须考虑地震、车辆等荷载引起的振动弹性波在高架桥结构中传播特性，保证振动的主要能量波能快速通过高架桥结构。否则，振动波能量急剧增加极易造成结构破坏。已有文献研究表明周期结构中存在能量带隙［1］，即某些频域内(通带域)的晶格波能在结构中传播，而有些频域内(禁带域)晶格波不能传播。因此，将等跨高架桥作为周期结构，利用声子晶体理论考察高架桥平面内振动能量带分布特征，将为结构的抗震设计、减振控制提供新思路。可通过合理设计周期性高架桥结构的几何、材料参数，保证地震波主要形式振动频率局陷于周期性高架桥结构能量带的禁带带隙范围内，从而有效抑制地震波引起的结构振动，避免造成结构破坏。

目前已有利用声子晶体结构理论进行两种或多种结构材料在不同方向的周期性特性分析。如一维周期性层状结构中振动波传播衰减特性及柱体材料、球形散射体埋入另一基体材料中形成的二、三维周期性点阵结构中弹性波传播特性研究［2－3］。对周期结构中能量带分析方法主要有传递矩阵法［2］、平面波展开法［4］、多重散射法［5］、时域有限差分法［6］及其它方法［7］等。考虑结构几何形式周期性，Mead等［8－9］采用自由波传递法分析刚、柔性支撑无限长周期梁的通带域禁带域，通过讨论周期梁结构多耦合振动能量带，认为平面内振动周期梁结构存在三种晶格波。文献［10］采用平面波展开法，利用二组元变截面构造周期结构细直梁，计算无限周期条件下细直梁弯曲振动中弹性波的能带结构。张小铭等［11］从振动功率流角度对周期简支梁振动特性进行分析，认为在带隙频率范围内振源不向梁输入功率流，从而能达到控制结构振动及噪声辐射。刘见华等［12］研究周期加筋板中弯曲波传播特性，并分析振动频率、弯曲波入射角对传播常数影响。文献［13］利用传递矩阵法，计算获得周期结构空腹梁的力传递率及带隙位置。考虑高架桥桥墩桩基础与半空间土体间耦合作用，文献［14］提出“开放式”周期性高架桥结构计算模型，并分析桩基础－土耦合作用对高架桥结构振动能量带分布影响。

对由桥墩、水平梁周期单元组成的高架桥结构，其形式与直线型周期结构不同，尤其桥墩－水平桥梁、水平桥梁－梁间接头存在，必引起振动弹性波在连接处跳跃。因此直线型周期梁能量带分析理论不能直接用于周期性高架桥结构。基于此，本文采用Bernoulli－Euler梁理论描述高架桥桥墩、水平桥梁平面内轴向、切向振动。考虑高架桥结构的水平梁－梁、水平梁－桥墩间弹簧连接，建立含水平梁、桥墩及弹簧接头的周期单元传递矩阵，利用Bloch理论结合周期结构几何特性，建立周期性高架桥结构平面内振动的能量带特征方程，分析高架桥桥墩－水平梁刚度比、弹簧刚度等对周期结构中晶格波传播影响。

1 周期性高架桥结构计算模型与传递矩阵

1.1 计算模型

对高架桥结构，采用简化物理模型将每跨轨道板、钢轨及扣件均复合为水平梁，相邻两轨道板间钢轨、轨道板与桥墩间支撑结构均简化为弹簧连接。由于高架桥桥梁桩基础刚度较大，地基沉降可忽略，因此可认为高架桥桥墩位于刚性基础上。等跨周期性高架桥结构的周期单元包括一个桥墩、左、右二水平梁及三个连接处弹簧，见图1。

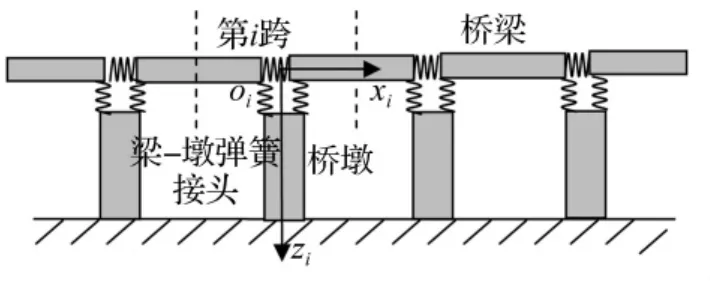
图1 刚性支撑、具有弹簧接头的周期性高架桥结构示意图Fig.1 A schematic illustration of a periodic viaduct with spring junction rigidly supported on a half space soil

当弹性波引起高架桥结构平面内振动时，任意第i根桥墩、水平梁z位置处3个内力分量轴力Nsi(z)、剪力Qsi(z)及弯矩Msi(z)与3个位移分量轴向、切向位移usi(z)、vsi(z)及转角θsi(z)形成状态矢量Ψsi(z)=［q(z)，f(z)］T。其中，fsi(z)=［Nsi(z)，Qsi(z)， Msi(z)］T;qsi(z)=［usi(z)，vsi(z)，θsi(z)］T;下标s=b时表示桥梁结构，s=d时表示桥墩结构。桥墩与桥梁结构内轴力、剪力及弯矩+、－号见图2。

周期性高架桥任意第i跨周期单元中，水平梁－水平梁间与水平梁－桥墩间弹簧连接头轴力、剪力及弯矩+、－号见图3。图中0－、0+分别表示弹簧接头左、右水平梁端;Nti，Qti，Mti分别为左、右水平梁端间弹簧接头轴力、剪力及弯矩;Nli，Qli，Mli，Nri，Qri，Mri分别为左、右水平梁端－桥墩间弹簧接头轴力、剪力及弯矩。

1.2 桥梁与桥墩传递矩阵

周期性高架桥结构产生平面内振动时，据Bernoulli－Euler梁理论，第i根桥墩、水平梁在频域内的振动控制方程［15］为

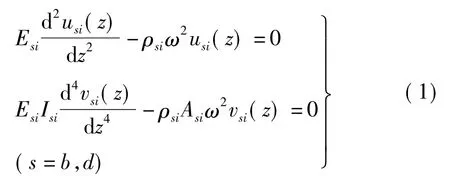
式中:ρsi，Asi分别为第i根桥墩、水平梁密度及横截面积;Isi为横截面转动惯量;Esi为结构杨氏模量。

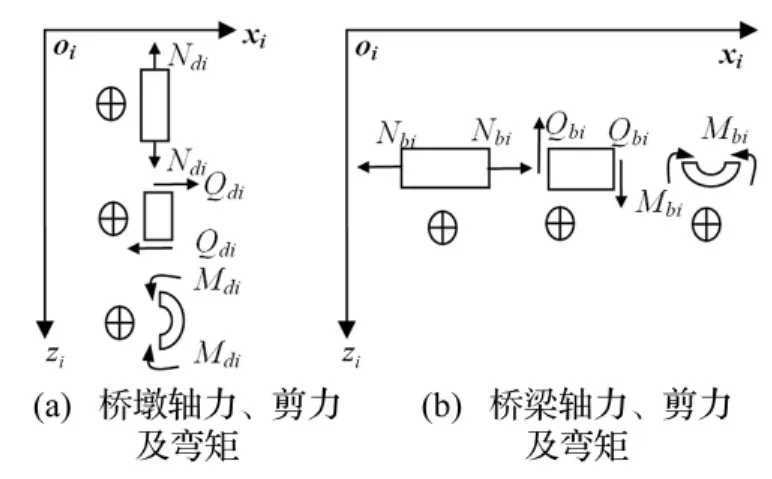
图2 高架桥结构内力符号规定Fig.2 The sign conventions for the internal forces of a pier and beam

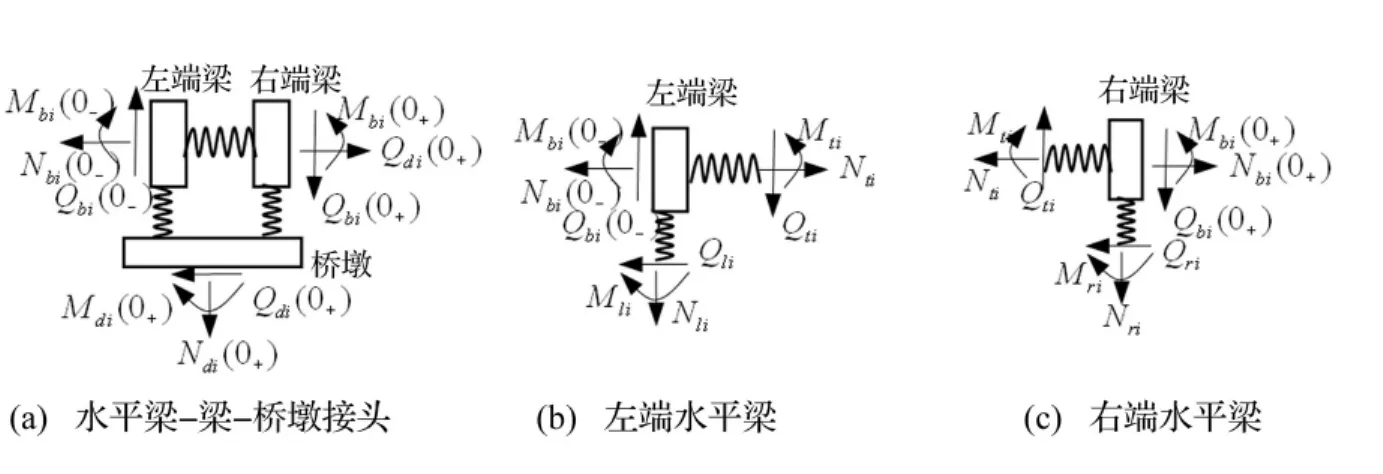
图3 平面内振动的高架桥桥墩与左、右端水平梁连接示意图Fig.3 The illustration for the junction linking the pier with the left as well as right beams undergoing in－plane vibration

由文献［16］可知，对考虑材料阻尼的线弹性结构，可采用复模量，即

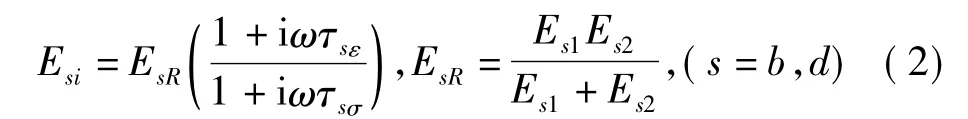
式中:τsε=ηs/Es2;τsσ=ηs/(Es1+Es2);且Es1，Es2及ηs分别为线弹性结构杨氏模量及粘性系数。

由控制方程(1)可得

1.3 周期性高架桥弹性接头传递矩阵

由图3(a)知，第n跨周期单元中左、右水平梁端间弹簧接头内力满足关系为

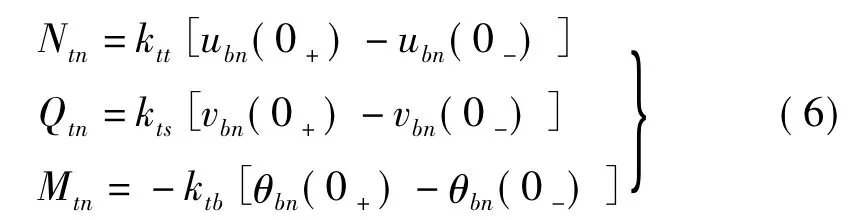
式中:ktt，kts，ktb分别为左、右水平梁端间弹簧接头轴向压缩、横向剪切及弯曲变形弹性刚度。

由图3(b)、(c)知，第n跨周期单元中左、右梁端－桥墩间弹簧接头内力为

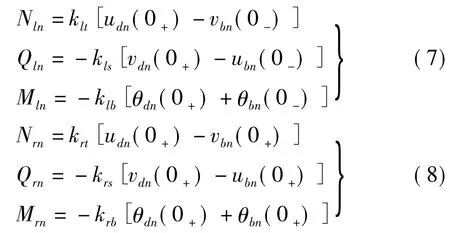
式中:klt，kls，klb，krt，krs，krb分别为左、右水平梁端－桥墩间弹簧接头轴向压缩、横向剪切及弯曲变形弹性刚度。

若不考虑弹簧接头质量，第n跨周期单元中左、右水平梁端－桥墩间弹簧接头满足的平衡条件为

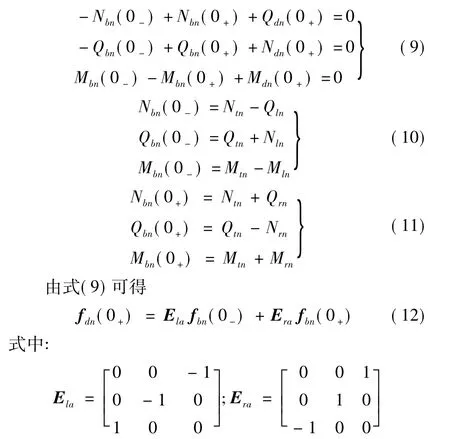
对第n个桥墩，由桥墩传递矩阵式(5)可得桥墩顶端与底部状态矢量间相互关系为

2 周期性高架桥本征方程

由式(21)、(24)可得第n跨周期单元左、右端水平梁状态矢量Ψbn(－Lb/2)、Ψbn(Lb/2)间关系为

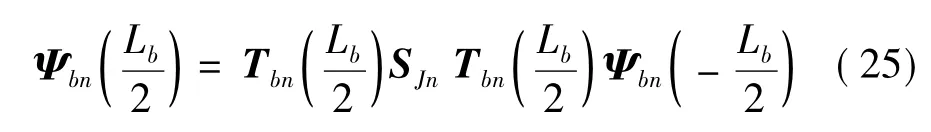
由此可知，考虑弹簧接头，第n跨周期单元传递矩阵Tcn为

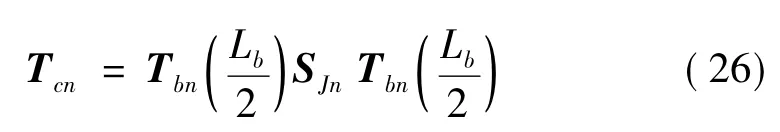
对周期性高架桥结构，每跨结构几何尺寸相同，据Bloch定理［7］可知

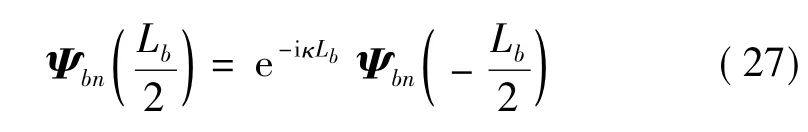
式中:κ为周期结构中传播波的晶格波数。

将式(27)代入式(25)，可得周期性高架桥结构平面内振动特征方程为

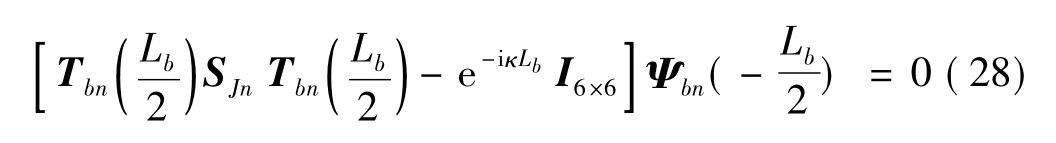
3 算例与数值分析

据文献［17］，由式(26)确定的第n跨周期单元传递矩阵Tcn为6×6矩阵可形成3对互为倒数的矩阵特征值，再由特征方程式(28)可得3对互为相反数的复晶格波κ，其中复晶格波实部表示在结构中传播波相变，虚部表示传播波衰减。利用文中模型，考察桥墩、水平梁弹簧等结构材料特性等对高架桥平面内振动能量带分布影响，在以下算例分析中，周期性高架桥的圆形桥墩、矩形横截面水平梁结构及接头弹簧的基本参数见表1、表2。

表1 桥墩、水平梁结构基本参数Tab.1 The values for the parameters of the piers and beams

表2 水平梁－梁、水平梁－桥墩间接头弹簧弹性刚度Tab.2 The value for the spring stiffness of beam-beam and beam-pier

3.1 与文献结果比较

为验证本文方法的正确性，考察周期性高架桥的水平梁－梁、水平梁－桥墩间刚性连接及平面内振动能量带分布情况，并与文献［14］结果比较。高架桥结构计算参数见表1。利用本文方法将具有刚性连接头的周期性高架桥传递矩阵式(20)代入本征方程式(27)，计算不同频率下周期性高架桥结构第一类复晶格波，见图4。其中水平梁、桥墩的粘弹性系数ηb=ηd=0。由图4看出，本文解与文献［14］结果几乎一致。

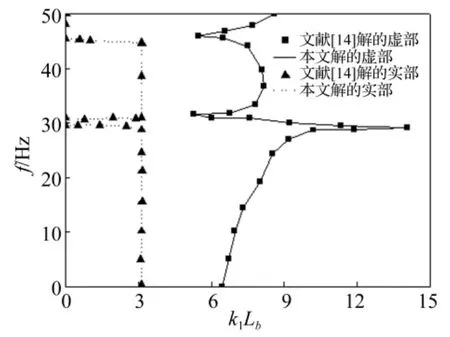
图4 具有刚性接头的周期性高架桥第一类晶格波Fig.4 The wavenumber for the first kind of lattice wave of in the periodic viaduct with rigidly junction case

3.2 水平梁与桥墩杨氏模量比影响

考察水平梁与桥墩的杨氏模量比对周期性高架桥能量带分布影响。计算中水平梁与桥墩的杨氏模量比分别为Eb/Ed=0.2，1.0，5.0，周期性高架桥的水平梁、桥墩及弹簧接头参数值见表1、表2。图5、图6为周期性高架桥结构平面内振动时水平梁内传播弹性波复晶格波数与频率间频散曲线。由二图看出，与周期性高架桥结构平面内轴向压缩、横向剪切及弯曲耦合振动相对应，沿水平梁传播的弹性波存在三种类型复晶格波:其中第一类复晶格波虚部较大(图5(a))，表明该类晶格波衰减较快，弹性波传播距离较短。第二类晶格波在计算频域内出现禁带域(Eb/Ed=5.0时f=0.0 ～8.0 Hz，12.0～28.0 Hz，42.0～50.0 Hz)与通带域(Eb/Ed=5.0时f=8.0～12.0 Hz，28.0～42.0 Hz)交替现象(图5(b))，在禁带域，由于同相反射波相互叠加，形成较强反射波，造成晶格波衰减较快;而在通带域，由于存在弹簧接头及水平梁内纵波与弯曲波(其中弯曲波又包括传播波、消散波［18］)的耦合作用，晶格波实部变化较大。第三类晶格波虚部除在0～5.0 Hz的较小频域区域及某些较窄高频段外，其余较宽频域段几乎为0(图5(c))，表明第三类晶格波在较大范围频率区域不发生衰减，且能在结构中传播更远。

由图6(a)、(c)可知，对第一、三类晶格波实部，除在较窄频域外几乎呈直线变化，其波速近似为与频率无关量。由图5可知，在计算频率域内，随Eb/Ed增大，第一类复晶格波虚部明显减小，第二、三类晶格波的禁带域数也在减小，尤其在高频区，第三类晶格波几乎为通带域。表明随水平梁刚度增加，在结构中传播的弹性波衰减较慢，传播距离会增大。

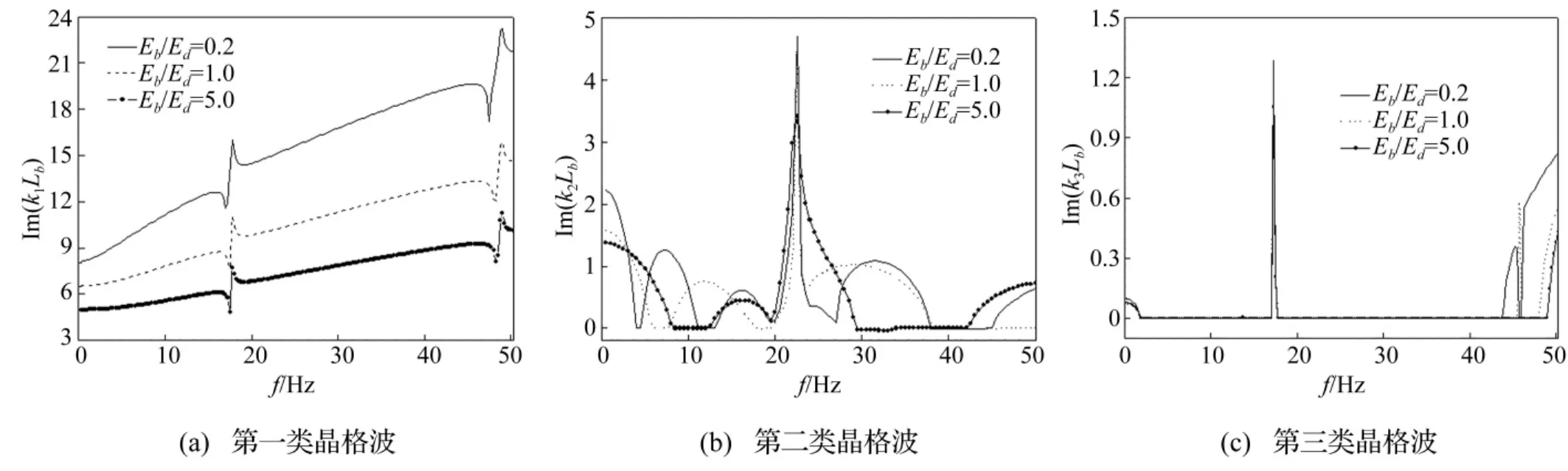
图5 不同水平梁－桥墩杨氏模量比时周期性高架桥结构中晶格波虚部Fig.5 The imaginary part of wavenumber for the lattice wave in the periodic viaduct with different value ofthe ratio of Young's modulus of the beams to that of the piers

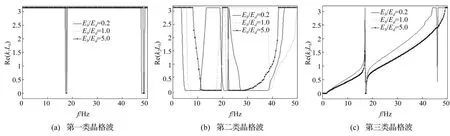
图6 不同水平梁－桥墩杨氏模量比时周期性高架桥结构中晶格波实部Fig.6 The real part of wavenumber for the lattice wave in the periodic viaduct with different value ofthe ratio of Young's modulus of the beams to that of the piers

3.3 接头弹簧刚度影响

考察水平梁－梁、水平梁－桥墩间接头弹簧刚度对周期性高架桥能量带分布影响。计算中水平梁－梁间接头弹簧刚度分三种情况，即Case 1:ktt=5.0×107N/m，kts=5.0×107N/m，ktb=1.0×107N/m;Case 2: ktt=5.0×108N/m，kts=5.0×108N/m，ktb=1.0×108N/m;Case 3:ktt=5.0×109N/m，kts=5.0×109N/m，ktb=1.0×109N/m。对每种计算情况，周期性高架桥结构、接头弹簧其它参数值见表1、表2。三种水平梁－梁间接头弹簧刚度计算情况下，周期性高架桥结构平面内振动时结构内复晶格波数随频率变化频散曲线见图7、图8。由二图看出，随水平梁－梁间接头弹簧刚度增大，第一类复晶格波波数虚部减小(图7(a))，第二晶格波通带域带宽增加，禁带域带宽减小(图7 (b))，Case 1时禁带域为f=5.8～19 Hz，而Case 3时禁带域为f=9～17 Hz，且禁带域内复晶格波数减小，第三类晶格波在高频区几乎为通带域，表明随水平梁－梁间接头弹簧刚度增大，结构中弹性波传播衰减减慢，弹性波传播距离增大。

针对左端水平梁－桥墩间接头弹簧刚度对周期性高架桥能量带分布影响，考察三种情况，即Case 1:klt=2.0×107N/m，kls=2.0×107N/m，klb=0.5×107N/m;Case 2:klt=2.0×108N/m，kls=2.0×108N/m，klb=0.5×108N/m;Case 3:klt=2.0×109N/m，kls=2.0 ×109N/m，klb=0.5×109N/m。每种计算情况下，周期性高架桥结构、接头弹簧其它参数值见表1、2。不同左端水平梁－桥墩间接头弹簧刚度计算情况下，周期性高架桥结构平面内振动时复晶格波数与频率间频散变化关系曲线见图9、图10。由二图看出，随左端水平梁－桥墩间接头弹簧刚度增大，第一类复晶格波虚部增大(图9(a))。第二类晶格波禁带域增宽(图9 (b))，在f=9～45 Hz范围内，Case 1中存在二个通带域，分别为f=18～20 Hz，f=39～45 Hz，而Case 3时几乎为禁带域，并随左端水平梁－桥墩间接头弹簧刚度增大该禁带域内晶格波虚部增大。在高频域，第三类晶格波虚部随左端水平梁－桥墩间接头弹簧刚度增大而增大，表明结构中弹性波衰减较快，振动传播距离降低。在较小频率范围内(0～10.0 Hz)，第二、三类晶格波禁带域与通带域交替出现，且随左端水平梁－桥墩间接头弹簧刚度增大通带域边缘频率增大(图9 (b))，在三种左端水平梁－桥墩间接头弹簧刚度情况下，第二类晶格波通带域边缘对应频率分别为4.0 Hz， 6.2 Hz，8.1 Hz。研究表明［1］，在通带域边缘存在类似周期结构缺陷态的平直带，表示弹性波在对应频率下出现局部化现象，引起能量集中。因此高架桥结构设计时，结构基本主频不能落在较小频率区间。

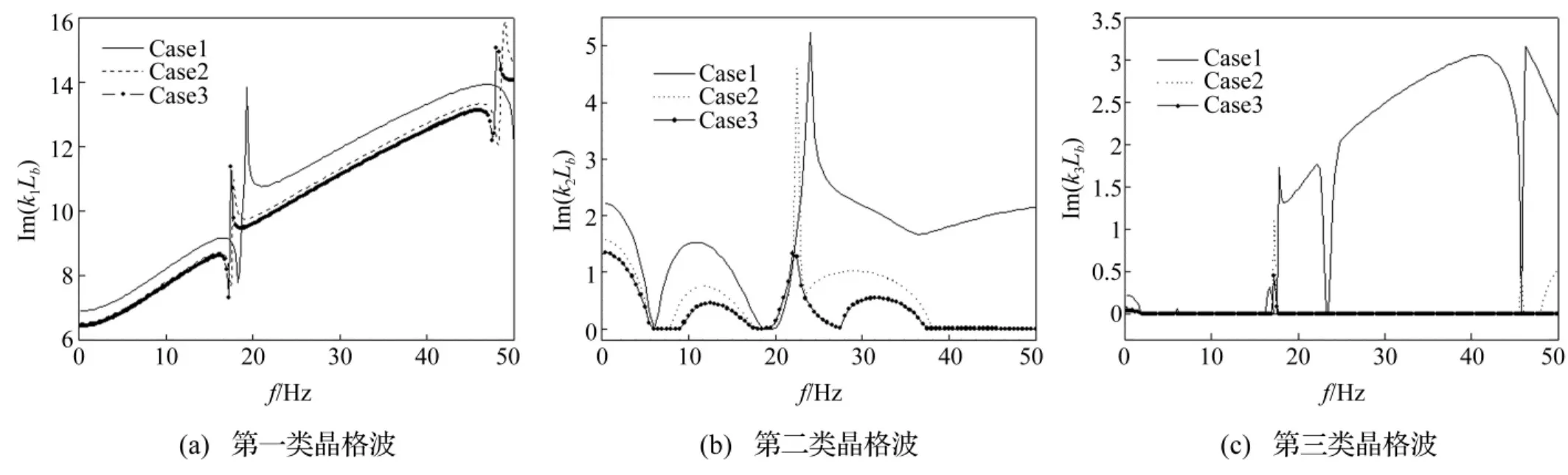
图7 不同水平梁－梁间接头弹簧刚度系数时周期性高架桥结构中晶格波虚部Fig.7 The imaginary part of wavenumber for the lattice wave in the periodic viaduct with different value ofthe stiffnesses of the beam－beam spring

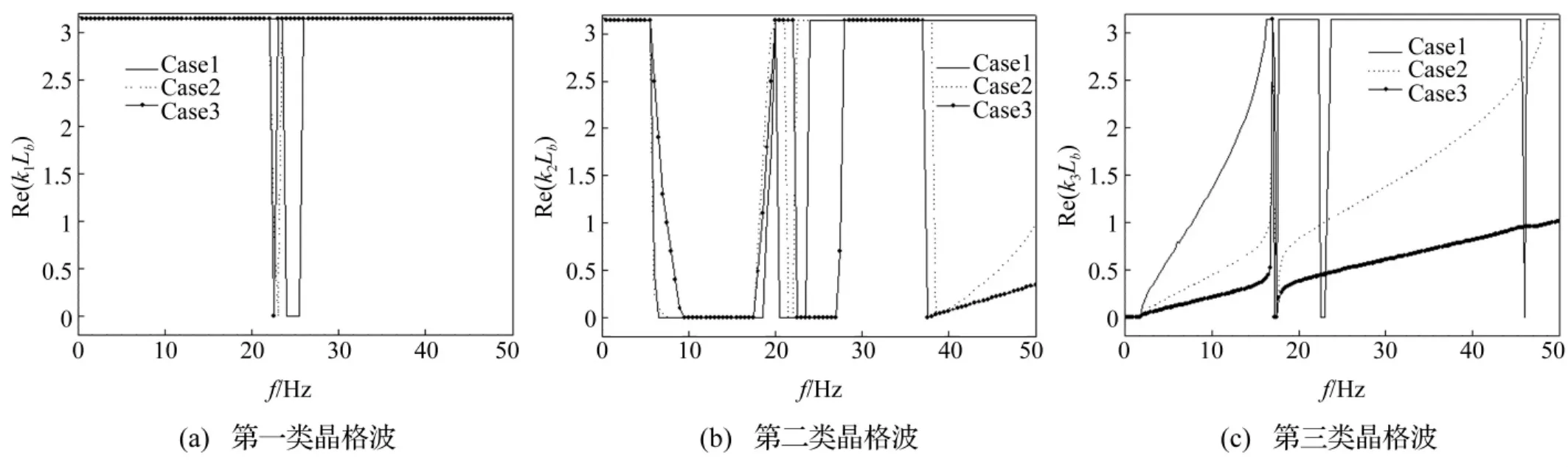
图8 不同水平梁－梁间接头弹簧刚度系数时周期性高架桥结构中晶格波实部Fig.8 The real part of wavenumber for the lattice wave in the periodic viaduct with different value of the stiffnesses of the beam－beam spring

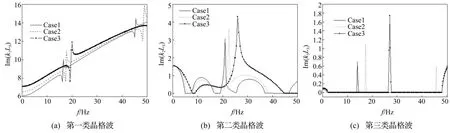
图9 不同左端水平梁－桥墩间接头弹簧刚度系数时周期性高架桥结构中晶格波虚部Fig.9 The imaginary part of wavenumber for the lattice wave in the periodic viaduct with different value ofthe stiffnesses of the left beam－pier spring

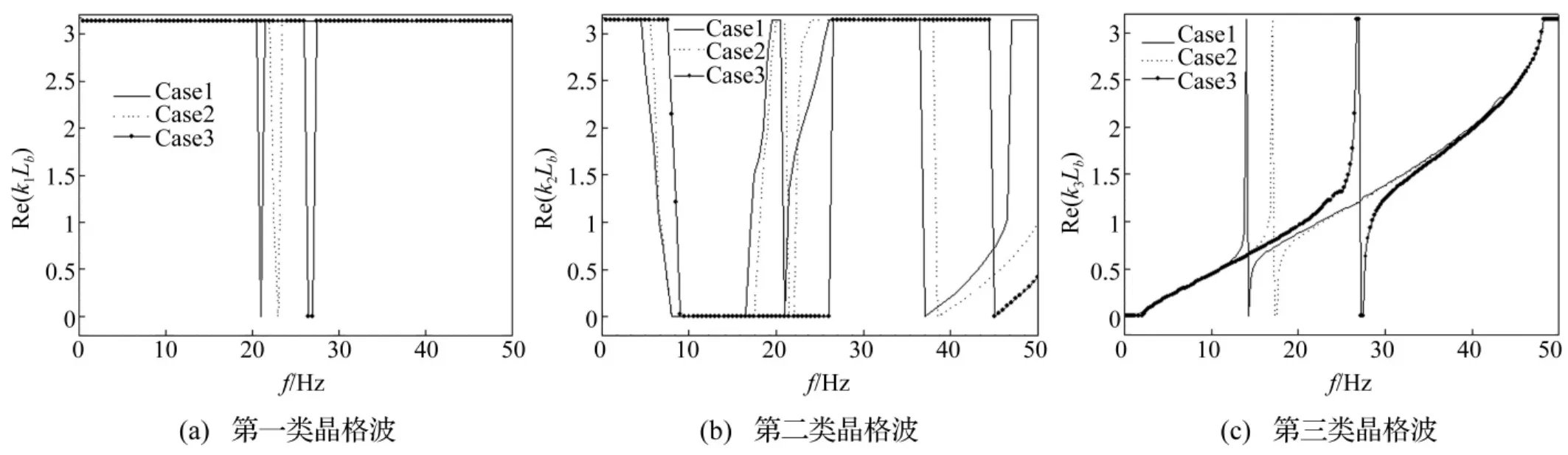
图10 不同左端水平梁－桥墩间接头弹簧刚度系数时周期性高架桥结构中晶格波实部Fig.10 The real part of wavenumber for the lattice wave in the periodic viaduct with different value ofthe stiffnesses of the left beam－pier spring

4 结论

本文通过考虑高架桥水平梁－梁及水平梁－桥墩间的弹簧连接，推导弹簧接头处的传递矩阵，建立周期性高架桥结构特征方程，并数值计算分析桥墩、水平梁弹簧等结构材料特性等对周期性高架桥平面内振动能量带分布影响，结论如下:

(1)具有水平梁－梁及水平梁－桥墩间的弹簧连接的周期性高架桥结构，平面内振动时结构中存在三种复晶格波。

(2)平面内振动的周期性高架桥结构内第一类晶格波沿高架桥结构衰减较快，沿结构传播距离较短;第二类晶格波，在计算频率范围内禁带域与通带域交替出现;若复晶格波虚部在较大频率区域内较小，表明结构中振动传播的为第三类晶格波。

(3)计算频率较小时，周期结构中三种晶格波的复波数较大，表明振动波难以沿周期结构传播，故高架桥结构设计时，基本主频不能在较小频率区域，否则极易引起能量集中，造成结构破坏。

(4)随周期性高架桥结构水平梁刚度、水平梁－梁弹簧接头刚度增大，高架桥结构中振动晶格波衰减减慢，振动波传播速度增大，振动传播距离亦增大。

(5)随水平梁－桥墩间弹簧接头刚度增大，结构中传播的复晶格波虚部增大，表明结构中振动波衰减更快些，振动传播距离亦会降低。

［1］温激鸿，韩小云，王刚，等.声子晶体研究概述［J］.功能材料，2003，34(4):364－367.

WEN Ji－hong，HAN Xiao－yun，WANG Gang，et al.Review of phononic crystals［J］.Journal of Functional Materials，2003，34(4):364－367.

［2］Sigalas M M，Economou E N.Attenuation of multiple scattered sound［J］.Europhysics Letters，1996，36:241－246.

［3］Mangaraju V，Sonti V R.Wave attenuation in periodic threelayered beams:analytical and FEM study［J］.Journal of Sound and Vibration，2004，276(3/5):541－570.

［4］Kushwaha M S，Halevi P，Dobrzynski L，et al.Acoustic band structure of periodic elastic composites［J］.Physical Review Letters，1993，71(13):2022－2025.

［5］Kafesaki M，Economou E N.Multiple－scattering theory for three－dimensional periodic acoustic composites［J］.Physical Review B，1999，60:11993－12001.

［6］Sigalas M M，García N.Theoretical study of three dimensional elastic band gaps with the finite－difference time－domain method［J］.Journal of Applied Physics，2000，87:3122－3125.

［7］Goffaux C，Sanchez－Dehesa J.Two－dimensional phononic crystals studied using a variation method:application to lattices of locally resonant materials［J］.Physical Review B，2003，67:144301.1.－144301.10.

［8］Mead D J.Free wave propagation in periodically supported，infinite beams［J］.Journal of Sound and Vibration，1970，11(2):181－197.

［9］Mead D J，Markus S.Coupled flexural longitudinal wave motion in a periodic beam［J］.Journal of Sound and Vibration，1983，90(1):l－24.

［10］温激鸿，郁殿龙，王刚，等.周期结构细直梁弯曲振动中的振动带隙［J］.机械工程学报，2005，41(4):1－6.

WEN Ji－hong，YU Dian－long，WANG Gang，et al.Elastic wave band gaps in flexural vibrations of straight beams［J］. Chinese Journal of Mechanical Engineering，2005，41(4):1－6.

［11］张小铭，张维衡.周期减支梁的振动功率流［J］.振动与冲击，1990，9(3):28－34.

ZHANG Xiao－ming，ZHANG Wei－heng.Vibrational power flow in a periodically supported beam［J］.Journal of Vibration and Shock，1990，9(3):28－34.

［12］刘见华，金咸定.周期加筋板中的弯曲波传播［J］.噪声与振动控制，2003，5:22－26.

LIU Jian－hua，JIN Xian－ding.The transmission of flexural wave through a periodic stiffened flat plate［J］.Noise and Vibration Control，2003，5:22－26.

［13］陈荣，吴天行.周期结构空腹梁的动态特性研究［J］.振动与冲击，2013，32(14):122－126.

CHEN Rong，WU Tian－xing.Dynamic characteristics of a periodic hollow beam［J］.Journal of Vibration and Shock，2013，32(14):122－126.

［14］Lu J F，Li J H，Jeng D S.A model for the energy bands of an“open”－type periodic structure:a periodic viaduct coupled with the half－space［J］.Acta Mech，2012，223(2):257－277.

［15］Graff K F.Wave motion in elastic solids［M］.New York: Dover Publication，1991.

［16］Carcione J.Wave fields in real media－wave propagation in anisotropic，anelastic and porous media［M］.Pergamon，Amsterdam，2001.

［17］Kittel C.Introduction to solid state physics［M］.New York: Wiley，1996.

［18］Mead D J.Waves and modes in finite beams:application of the phase－closure principle［J］.Journal of Sound and Vibration 1994，171(5):695－702.

附录:

Analysis of energy bands of periodic viaduct with pier-beam spring junction undergoing in-plane vibration

XU Bin，XU Man－qing
(Department of Civil Engineering，Nanchang Institute of Technology，Nanchang 330029，China)

The periodic viaduct was modeled to be composed of an infinite number of spans，and each span was supposed to consist of one pier，two longitudinal beams and three linking springs.Based on the Bernoulli－Euler beam theory and Bloch theorem，a transfer matrix for the junction linking beams and pier was provided.The polynomial eigenvalue equation for the energy bands of the periodic viaduct undergoing in－plane motion was also derived.Based on the obtained eigenvalue equation，the energy bands of the periodic viaduct were solved.With the proposed model，the influences of the ratio of Young＇s modulus of beams to that of piers and the stiffness of springs on the energy bands of the periodic viaduct were investigated.The numerical results demonstrate that when the periodic viaduct with beam－beam and beam－pier spring junctions is undergoing in－plane motion，there exist three lattice waves corresponding to axial compression，transverse shear and bending vibration respectively:the first kind of lattice wave is a highly decaying wave and cannot propagate a long distance along the viaduct;the second kind of lattice wave can propagate only in some frequency ranges;and the third kind of lattice wave can propagate at most of frequencies except in a certain lower frequency range.As a result，it is crucial in the design stage to guarantee the dominant structural frequency of the viaduct not to be located within this low frequency range.Otherwise，most energy of seismic waves will be concentrated，which is dangerous for the viaduct.Moreover，with increasing the ratio of Young＇s modulus of the beams to that of the piers and the stiffness of the beam－beam spring，the attenuation of the lattice waves decreases significantly，implying that the wave can propagate a longer distance along the structures.

periodic viaduct;transfer matrix;Bloch theorem;lattice waves;spring junction

TU375.4

A

10.13465/j.cnki.jvs.2015.02.022

国家自然科学基金资项目(51269021);江西省自然科学基金重点项目(20133ACB20006);江西省普通本科高校中青年教师发展计划访问学者专项资金项目资助

2013－07－24修改稿收到日期:2014－01－15

徐斌男，博士，副教授，1971年生