面向SOMS外包任务分配决策的一对一Stackelberg博弈模型研究

周光辉，程远森，朱家凯

1.西安交通大学机械制造系统工程国家重点实验室，陕西西安 710049 2.西安交通大学机械工程学院，陕西西安 710049

面向SOMS外包任务分配决策的一对一Stackelberg博弈模型研究

周光辉1，2，程远森2，朱家凯2

1.西安交通大学机械制造系统工程国家重点实验室，陕西西安 710049 2.西安交通大学机械工程学院，陕西西安 710049

为解决服务型制造系统（service-oriented manufacturing system，SOMS）中的核心企业外包任务面向单一供应商的分配决策问题，提出并建立了一对一Stackelberg外包任务分配决策博弈模型。在该博弈模型中，将核心企业映射为领导者，将供应商映射为追随者，将生产成本与利润分别映射为核心企业与供应商的收益函数。为实现一对一Stackelberg博弈模型Stackelberg均衡点的有效求解，设计了2层次嵌套遗传算法（genetic algorithm，GA）。案例仿真结果验证了所提出的模型与解算方法的正确性。

服务型制造；Stackelberg博弈；Stackelberg均衡；遗传算法

服务型制造（service-oriented manufacturing，SOM）是以制造服务外包和提供产品整体服务解决方案为显著特征的、实现制造和服务有机融合的新型制造模式，通过产品和服务融合、客户全程参与、企业相互提供生产性服务与服务性生产，实现分散制造资源的整合和各自核心竞争力的高度协同，最终实现制造价值链中各利益相关者的价值增值［1-3］。在产品加工制造环节，其显著特征是在核心企业控制下的“JIT（just-in-time）外包＋自主核心加工＋（近）零库存”的跨企业生产，制造服务及所形成的制造服务产业链为制造企业拓展了新的利润空间。知名跨国企业（GE／GM／Boeing／IBM）、国内长三角（如苏州工业园区企业集群）、珠三角区域（如富士康集团）等均涌现出了SOM的实践模式。服务型制造系统（service oriented manufacturing system，SOMS）作为SOM的外在物理表现模式，由于SOM的市场先行特征，使得SOMS配置成为践行SOM的热点与难点问题之一。而在“产品加工制造”环节，SOMS配置的核心问题就是解决JIT生产模式下的核心企业和供应商的外包任务的分配决策问题。SOMS中，由于JIT生产与（近）零库存两大特征的引入，使得交货期与库存成本成为影响外包任务分配决策的核心因素［4-5］，传统的外包任务分配决策模型［6-7］与算法难以解决SOMS的外包任务分配决策问题。据此，本文以解决SOMS的“产品加工制造”环节中核心企业的特定外包任务面向单一供应商的分配决策问题为目标，采用博弈理论，建立了一对一Stackelberg外包任务分配决策博弈模型，设计了2层次嵌套遗传算法（genetic algorithm，GA）对模型进行了有效解算，最后以齿轮零件的生产外包为例进行了有效性验证。

1 外包任务分配决策问题描述

本文重点解决核心企业外包制造任务面向单一供应商的分配决策问题。该问题描述为：核心企业存在一个或一批特定的外包制造任务，面向单个供应商进行外包。在任务外包活动中，核心企业以最小化生产成本为目标、供应商以最大收益为目标，双方共同进行分配决策，最终达到双方利益均衡的任务分配决策方案。

在该问题中，基于JIT思想，分别引入核心企业的最佳接货期、供应商的期望交货期以及独立于核心企业与供应商的第三方库存的概念与思想，来分析并建立外包任务分配决策问题模型。在描述问题模型之前，首先对如下参数与变量进行定义：

1） Y—核心企业的订单总量；

2） P—供应商的报价；

3） T0—核心企业的最佳接货期；

4） T—供应商的期望交货期；

5） Tmin—核心企业的接货期接受区间下限；

6） Tmax—核心企业的接货期接受区间上限；

7） tmin—供应商的交货期接受区间下限；

8） tmax—供应商的交货期接受区间上限；

9） t—供应商的交货期；

10） Δt—供应商的交货期调整量Δt＝t－T；

11） u0—交货期变化引起核心企业生产成本的损失系数；

12） dm—核心企业到第三方库存的运输距离；

13） dp—供应商到第三方库存的运输距离；

14） φ—运输成本费率；

15） σ0—核心企业第三方库存费用所占的比重；

16） h—第三方库存的库存费率；

17） C—核心企业的订购周期；

18） D—核心企业的日需求量；

19） α—库存安全系数；

20） Y0—第三方安全库存量Y0＝α·Y；

21） K—供应商原材料的采购成本费率；

22） Ψ—供应商原材料与对应产品间转化系数；

23） q—除一次性惩罚金额外的拖期惩罚费率；

24） V—供应商加工成本费率；

25） ε0—在制品库存的成本费率；

26） ω0—供应商标准在制品持有量；

27） ω—供应商在制品持有量；

28） a—拖期一次性惩罚；

29） MINp—供应商的期望收益；

30） MAXm—核心企业的期望成本。

核心企业的最佳接货期T0与供应商的期望交货期T与核心企业和供应商的利润密切相关。图1分别描述了核心企业最佳接货期及可接受时间窗、供应商的期望交货期与允许时间窗的关系。设供应商根据其生产能力和利润目标对交货期的调整量为Δt，则供应商的实际交货期为t＝（T＋Δt）。

图1 核心企业和供应商的接、交货时间窗

核心企业的最佳接货期T0与供应商的期望交货期T均是根据核心企业的生产计划确定的。供应商交货期离期望交货期越远，核心企业付出的生产成本越大。假设供应商根据自己的生产能力和利润目标对交货期的调整量为Δt，那么实际交货期为t＝（T＋Δt）。采用威布尔分布函数计算核心企业关于交货期的成本函数如下式所示：

影响外包任务在制品第三方库存成本的主要因素包括交接货期、制造周期、库存价格、运输距离、库存量、库存服务质量等因素。外包任务在制品第三方库存的总成本函数常呈U型分布如图2所示。

图2 外包任务在制品持有成本函数

根据外包任务在制品第三方库存的持有成本函数特性，采用威布尔分布函数对其描述如下：

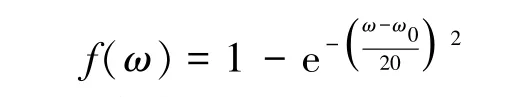
式中标准在制品库存量ω0由核心企业的生产计划及供应商的实际生产节拍确定。

在JIT生产模式下，核心企业为实现近零库存生产，会根据生产需要，小批量、高频率的向供应商订货，据此可得出第三方库存水平如图3所示。

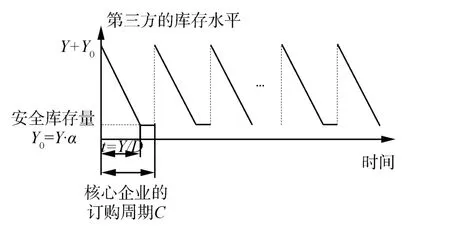
图3 外包任务在制品的第三方库存水平

依据图3可得出第三方的库存总费用为h· （Y0·C＋Y2／（2D）），该费用由核心企业和供应商共同承担。

2 一对一Stackelberg外包任务分配决策博弈模型

Stackelberg博弈模型是一个双寡头模型，领导者（leader）和追随者（follower）行动有先后顺序，领导者先行决策，追随者根据领导者决策结果再作决策，最终达到均衡目标［8-10］。据此，围绕本文提出的外包任务分配决策问题，建立了一对一Stackelberg博弈模型。在该模型中，将核心企业映射为领导者，供应商映射为追随者；将核心企业外包任务的成本函数与供应商的利润函数分别映射为各自的收益函数。建立具体的博弈模型为如下三元组：式中：El表示核心企业，Ef表示供应商；Sl为El的策略集，Sf为Ef的策略集，其中，Sl为核心企业针对外包任务，根据其生产计划而面向供应商的期望交货期，Sf为供应商在约束条件下针对外包任务的报价和交货期调整量；Ul为El的收益函数，Uf为Ef的收益函数，分别对应核心企业生产成本与供应商收益。

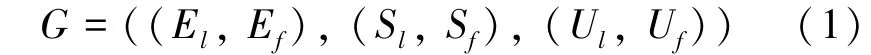
核心企业的采购成本：

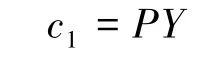
核心企业关于交货期的损失成本：

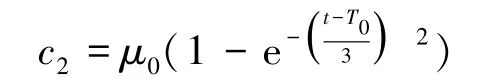
核心企业的运输成本：

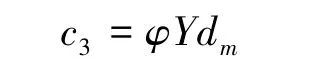
核心企业的第三方库存成本：

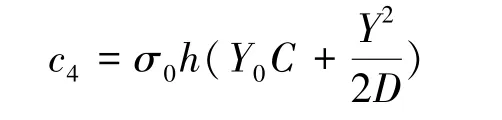
据此，得出核心企业的总生产成本如下：

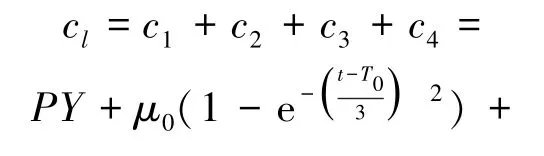
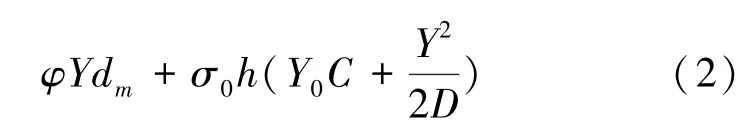
核心企业的收益函数式为

供应商的收益应从外包任务交易收入中扣除拖期惩罚费用、提前完工库存费用、拖期一次性惩罚、生产成本（原材料采购成本、运输成本、加工成本、在制品库存成本）以及竞标成本。供应商的具体利润采用式（4）表示：

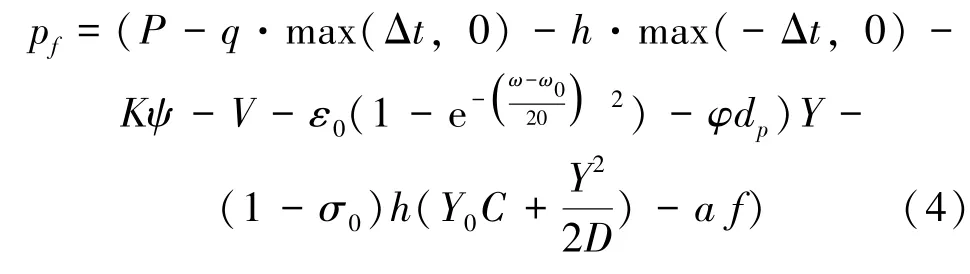
据此得出供应商的收益函数式如下：

式（1）～（5）满足如下约束条件：

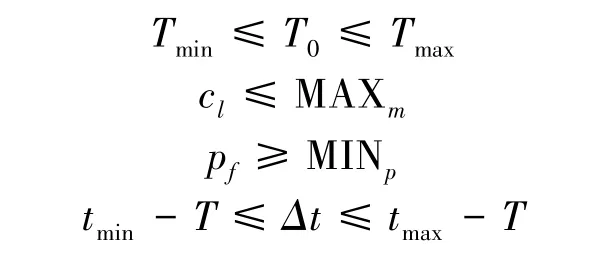
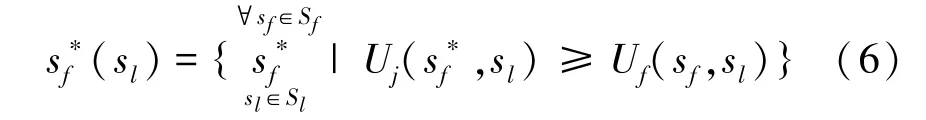
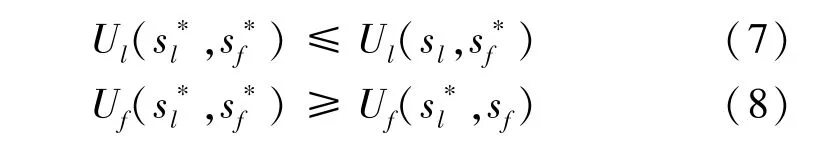
3 两层次嵌套GA的博弈模型求解

为实现对上述一对一Stackelberg博弈模型的有效求解，考虑到单层标准GA存在的不足，设计了2层次嵌套GA［11－12］来协同求解该博弈模型的均衡解。其中，上层GA（领导者GA）用于求解核心企业的最优生产成本、下层GA（追随者GA）用于求解供应商的最优利润，上下两层GA协同工作，最终得出Stackelberg均衡解。上层GA采用二进制编码、比例选择、单点交叉和基本位变异，下层GA采用实数编码、比例选择、实数交叉和基于概率的实数变异。上下两层的适应度函数分别设计为

图4 两层次嵌套GA求解Stackelberg博弈模型算法流程

4 实例仿真与分析

为验证所提出的面向SOMS外包任务分配决策的一对一Stackelberg博弈模型和2层次嵌套的GA求解算法的有效性，采用数控珩磨机生产中的齿轮零件的外包来进行案例仿真分析。宁夏大河机床有限公司为数控珩磨机生产的核心企业，西安法士特齿轮有限公司为珩磨机齿轮零件的外包供应商。定义该博弈模型的具体参数赋值见表1。

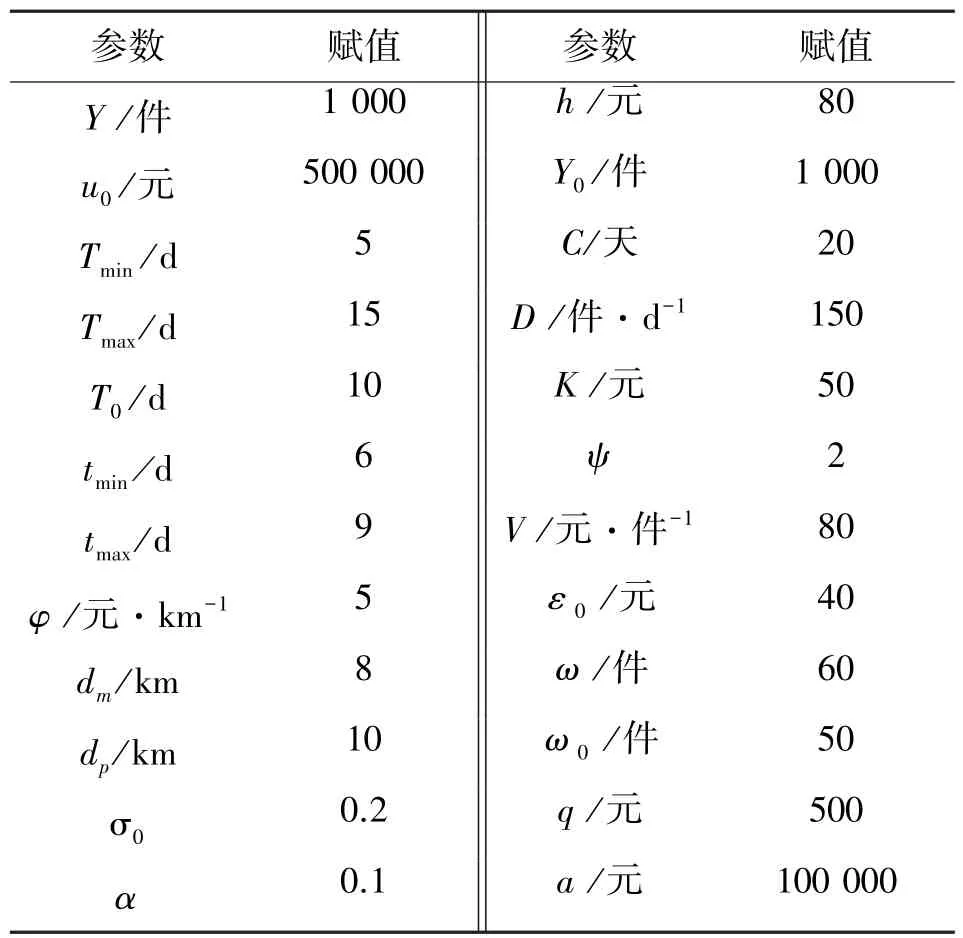
表1 一对一Stackelberg博弈模型参数赋值

将以上参数分别代入式（2）、（4）得到：

应用上述2层次嵌套GA对算例进行了解算，设定上下层GA的交叉概率分别为0.5、0.7，变异概率分别为0.007、0.01，种群规模分别为30、100，进化代数分别为50、80，阈值分别ξl＝0.001、ξf＝3。算法进化过程如图5所示。表2为求得的齿轮外包任务一对一Stackelberg博弈均衡点参数方案集及对应的最佳收益值。

图5 遗传算法进化过程

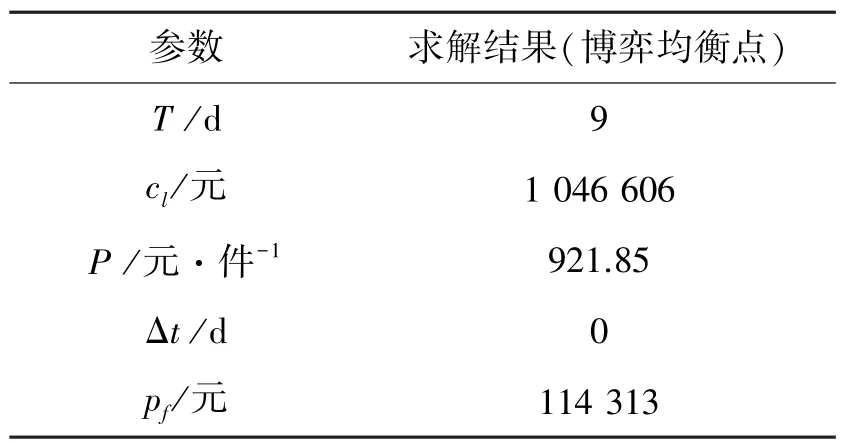
表2 齿轮外包任务Stackelberg博弈均衡点方案与收益值

由表2看出，在求得的Stackelberg博弈均衡点上，宁夏大河机床有限公司给出的齿轮零件外包加工任务的期望交货期为9d，得出的最小生产成本cl为1 046 606元；西安法士特齿轮有限公司的报价为921.85元，并能满足宁夏大河机床有限公司的期望交货期，其利润值pf为114 313元。核心企业为了满足自身的生产需求，会给出接近最佳交货期的期望交货期，供应商则根据本企业实际生产能力和期望交货期对交货期进行调整；经过不断地交互，最终实现了核心企业和供应商的利益均衡决策。仿真结果符合实际情况，说明了模型和算法的正确性和可行性。

5 结束语

本文围绕SOMS环境下外包任务的一对一分配决策问题进行了深入研究，采用博弈理论建立了一对一Stackelberg外包任务分配决策博弈模型并设计了双层次嵌套GA求解算法对模型进行了有效求解。具体的仿真案例分析结果表明提出的博弈模型和求解算法可以很好完成SOMS环境下外包任务的分配决策问题。论文的研究为SOM模式与系统的发展与实践提供了理论、方法与技术支持。

［1］汪应洛.发展服务型制造业的战略思考［R］.管理科学与管理工程院士学术报告会.顺德，2007.

［2］孙林岩，高杰，朱春燕，等.服务型制造：新型的产品模式与制造范式［J］.中国机械工程，2008，19（21）：2600-2604.

［3］孙林岩，李刚，江志斌，等.21世纪的先进制造模式-服务型制造［J］.中国机械工程，2007，18（19）：2307-2312.

［4］郑力，江平宇，乔立红，等.制造系统研究的挑战和前沿［J］.机械工程学报，2010，46（21）：124-136.

［5］SHENW，XUE Y，HAO Q，et al.A service-oriented sys-tem integration framework for community-based independent living spaces［C］／／IEEE Anchorage，Alaska，USA，2011：2626-2631.

［6］杨春晖，周国华.基于资源型供应链的企业决策问题研究［J］.统计与决策，2014（5）：179-182.

［7］欧阳浩，王智文，陈波，等.基于Excel数据挖掘实现制造企业的决策支持［J］.制造业自动化，2014（5）：109-113.

［8］周光辉，王蕊，江平宇，等.作业车间调度的非合作博弈模型与混合自适应遗传算法［J］.西安交通大学学报，2010，44（5）：35-39.

［9］宿洁.OEM业务的Stackelberg博弈策略与算法［J］.计算机工程与应用，2008（21）：227-230.

［10］吴辉球，李艳，罗云峰.基于竞赛模型的外包服务竞争建模［J］.武汉科技大学学报，2008，10（6）：29-32.

［11］李昌兵，袁浩，杜茂康.基于层次遗传算法的非线性双层规划问题求解策略［J］.系统工程，2011，29（4）：109-113.

［12］李宏，王宇平.解非线性二层规划的一种混合遗传算法［J］.西安电子科技大学学报，2002，29（6）：840-843.

Research on the one-to-one Stackelberg gamemodel facing the allocation decision of SOMS outsourcing tasks

ZHOU Guanghui1，2，CHENG Yuansen2，ZHU Jiakai2
1.State Key Laboratory for Manufacturing Systems Engineering，Xi’an Jiaotong University，Xi’an 710049，China 2.School of Mechanical Engineering，Xi’an Jiaotong University，Xi’an 710049，China

For solving the allocation decision-making issue of the core enterprise’s outsourcing tasks facing sin-gle supplier in the service-oriented manufacturing system（SOMS），a one-to-one Stackelberg gamemodel was put forward.In the Stackelberg gamemodel，the leader corresponds to the core enterprise and the follower cor-responds to the supplier；a payoff function of the core enterprise and supplier was defined as production cost and profit，respectively.In order to seek for an effective solution of Stackelberg equilibrium point in the one-to-one Stackelbergmodel，a two-level nested genetic algorithm（GA）was designed.Case simulation result dem-onstrates the accuracy of the presented gamemodel and its related algorithm.

service-oriented manufacturing；Stackelberg game；Stackelberg equilibrium；genetic algorithm

TH181；TH186

A

1009-671X（2015）02-053-05

10.3969／j.issn.1009-671X.201406013

2014-06-18.

日期：2015-03-25.

国家自然科学基金资助项目（51175414）；教育部新世纪优秀人才支持计划项目（NCET-12-0452）；国家科技支撑计划资助项目（2012BAH08F02）.

周光辉（1972-），男，教授，博士生导师，博士.

周光辉，E-mail：ghzhou＠mail.xjtu.edu.cn.

http：／／www.cnki.net／kcms／detail／23.1191.u.20150325.1313.016.html